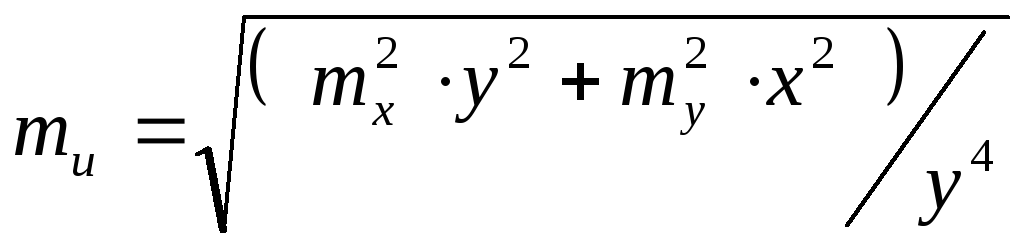Пояснения и указания по выполнению задания

1. Способы определения площадей земельных участков

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного, городского кадастра и землеустройства.

В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют различные способы определения площадей:

1. Аналитический, когда площадь вычисляется по результатам измерений линий на местности, по результатам измерений линий и углов на местности или по их функциям (координатам вершин фигур).

2. Графический, когда площадь вычисляется по результатам измерений линий или координат на плане (карте) или с помощью приспособлений (палеток).

3. Механический, когда площадь определяется по плану с помощью специальных приборов (планиметров).

Иногда эти способы применяют комбинированно, например, часть линейных величин для вычисления площади определяют по плану, а часть берут из результатов измерений на местности.

При аналитическом способе определения площадей (по результатам измерений на местности) применяются формулы геометрии, тригонометрии и аналитической геометрии.

При определении площадей графическим способом (по результатам измерений на карте) также используют формулы простых геометрических фигур, если данный участок имеет прямолинейные границы.

Если же требуется определить площадь земельного участка с криволинейными границами, используют специальные приборы – планиметры, и приспособления - палетки.

2. Основы оценки точности площадей земельных участков

Площади земельных участков вычисляют, используя результаты измерений, выполненных на местности или картографических материалах (планах, картах). Измеряемыми величинами в зависимости от выбранного способа являются координаты, разности координат, горизонтальные углы, расстояния и другие величины. Таким образом, вычисляемые площади представляют собой функции результатов измерений. Ошибки в результатах измерений сказываются на точности вычисления площадей.

В качестве обобщенной характеристики точности измерений принимают среднюю квадратическую погрешность (ошибку).

Поскольку в практике геодезических работ искомые значения получают в результате вычислений как функции измеренных величин, результаты будут содержать ошибки, значения которых зависят от вида функции и от ошибок аргумента.

Например, для алгебраической суммы z = x + y + … + t средняя квадратическая ошибка вычисляется по формуле:

Для линейной функции z = k₁x₁ +k₂x₂ + … + k_nx_n, где k₁, k₂, …, k_n – постоянные коэффициенты, среднюю квадратическую ошибку вычисляют по формуле:

Для функций нескольких независимых величин z =f( x, y,…, t) определяют по формуле:

Формулы для вычисления средней квадратической ошибки в зависимости от вида функции приведены в табл. 2.1.

Таблица 2.1

Средняя квадратическая ошибка функции

Функция	Средняя квадратическая ошибка функции
U = k∙x, где k – безошибочное постоянное число; x – аргумент, полученный из измерений	mu = k∙mx
2. U = х + у
3. U = x-y
4. U = k1∙x+k2∙y+…+kn∙w
5. U = x∙y
6. U = x/y

Например, если площадь треугольника была вычислена по формуле:

, то средняя квадратическая ошибка определения площади будет вычисляться по формуле:.

Среднюю квадратическую ошибку называют абсолютной.

Отношение абсолютной ошибки к среднему значению измеренной вели­чины, выраженное дробью с числителем, равным 1, называют относительной ошибкой. Знаменатель относительной ошибки целесообразно округлять до целых десятков, если он выражается в сотнях, до сотен, если он выражается в тыся­чах и т.д.

Например, средняя квадратическая ошибка определения площади земельного участка на карте М 1:5000 m_Р = ±0,5м (графическая точность), Р=1243,0м², тогда относительная погрешность .

Для получения значения относительной погрешности в виде аликвотной дроби достаточно числитель и знаменатель поделить на числитель.