Блочный шифр

ключи ;

числа

-сообщение ,

Кодировка : -криптограмма

декодирование:

Криптоанализ: 1 уровень –чисто переборная задача

~

гипотеза ~

перебирает все

3 уровень - -известно

-прослушиванием

Взламывается за полиномиальное время.

Обобщение модулярного принципа шифрации.

Рандомизированные ключи:

ядерный ключ

модули и их порядок следования

: ,

- большое число (ограниченное позже)

,

Сообщение :

t битный

Кодирование:

Декодирование:

*

Модулярный аналог P системы.

Интимный ключ:

;

ядерный ключ ,

:

:

открытый ключ

: ,

Кодирование:

сообщение , битный блок

-криптограмма

Декодирование:

*

,

Появилась возможность строить “блуждающий” открытый ключ

Лекция №16

-схема разделения секрета

Используется в различных протокольных схемах;

Определение: -участников:

-секрет (представлен в цифровой форме)

задается комбинацией “компонент” (в цифровой форме)

каждому участнику известна только приданная ему компонента : ,

участники могут объединяться в группы.

Эти группы стремятся раскрыть секрет (объединять, чтобы узнать инструкции, записанные в секрете С)

Условия вскрытия секрета C:

любые участников, объединенные в группу по комплексу известн. им информации могут вскрыть секрет , независимо от оставшихся участников (или более )

любые или менее не в состоянии вскрыть секрет

Такая схема разделения секрета называется -схемой.

Иллюстрация: в математике существует довольно много объектов, описываемых своими компонентами, причем если компонентов , то объект определяется единственным образом, в противном случае – объект недоопределяется.

Замечание: если число компонент превышает , то объект определяется (задается) избыточно, в противном случае объект недоопределен.

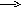
в этой системе точка задает 3-и координаты –избыточно, в плоскости она единственным образом определяется 2^мя координатами.

Построение -схема разделения секрета на основе модулярной арифметики.

Имеется попарно взаимно-простых модулей.

секрет есть число (код секрета) расположенные в диапазоне

имеется участников

каждому участнику , известна (и только ему) информация , где

Вопрос: при каких ограничениях на рассматриваемая группа участников образуют -сх. разделения секрета

Решение: 1. упорядочим модули :

? каким д.б. , чтобы любые участников могли вскрыть секрет.

Чтобы любые участников могли вскрыть секрет достаточно, чтобы

Для того чтобы любые участников не могли вскрыть секрет достаточно, чтобы

пусть модули и число удовлетворяло услов. -сх. разделения секрета, тогда объединение любых участников:

-это условие выполняется т.к.

Какова степень неопределенности в формировании секрета у участников?

0 D

- переводят эту комбинацию в полиадический код.

∆-алгоритм

старшая цифра полиад.

кода.

степень неопределенности характеризуется , где модуль не вошедший в состав

какие ограничения на выбор оснований необходимо дополнительно наложить, чтобы степень неопределенности была равномерно разделена между участниками разделения секрета?

Необходимо чтобы

,