Защита информационных процессов.

Амербаев Вильжан Мавлютинович, факультет мПиТк, 4й курс 2й семестр

лекции набирали Артем (Alfred) и Сергей летом 2002 год, за что им вечная память 

Лекция №1

Архитектура блочных шифров.

Множество G – алгебра с двумя бинарными операциями:  .

: G²G : G²G

a  b = c  a = c  b – связь между операциями П: a + b = c a = c - b ассоциативная

ab = c a = c/b. коммутативная

Замечание: в общем случае операцииине обладают свойствами коммутативности и дистрибутивности.

defОперацияназывается правой обратной операцией по

отношению к прямой операции .

Блочные шифры (итеративные).

Символами алфавита сообщений и криптограмм служат элементы множества G.

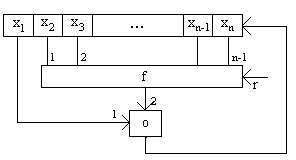
(1) x₁,x₂, …x_n,x_n+1, … ,x_n+k, … - последовательность, порождаемая рекурсивной процедурой порядкаn,x_i G.

(x₁,x₂, …x_n) – начальный отрезок последовательности (1).

x_n+1 = x₁  f₁(x₁, …, x_n, r₁), f₁: GⁿG

(2) x_n+2 = x₂  f₂(x₃, …, x_n+1, r₂), f₂: GⁿG

…………………………………………..

x_n+k = x_k  f_k(x_k+1, …, x_n+k-1, r_k) f_k: GⁿG

Последовательность (1) называется орбитой системы (2).

Если оборвать последовательность (1), то последние nэлементов этой последовательности будутконечнымотрезком орбиты.

Если при этом начальный отрезок (x₁,x₂, …x_n) совпадает с конечным отрезком (x_m,x_m+1, …,x_m+n-1), то такая орбита называетсяциклом.

Наименьшая длина циклической орбиты называется периодом.

Свойство инволятивности системы (2)

Рассмотрим частный случай: n=2,

начальный отрезок <x₁,x₂>

переход x₃=x₁f₁(x₁,r₁)r_i– ключи, известные

называется раундомx₄=x₂f₂(x₃,r₂) параметры

x₅ = x₃  f₃(x₄, r₃)

x₆ = x₄  f₄(x₅, r₄)

x₇ = x₅  f₅(x₆, r₅)

конечный отрезок <x₆,x₇>

x₅ = x₇  f₅(x₆, r₅)

x₄=x₆f₄(x₅,r₄) обобщенная схема Фейстельа:

x₃ = x₅  f₃(x₄, r₃)     

x₂ = x₄  f₂(x₃, r₂) f₁ = f₂ =…= f₅

x₁ = x₃  f₁(x₂, r₁)

f_i – функции шифрования.

в данном случае символ композиций

_ _

Cиеннон:C=(L₁R₁T₁)(L₂R₂T₂)…(L_n  R_n  T_n)S

блоки операция

R– блок перемешивания

T– блок рассеивания

Устойчивая криптосистема создается тогда, когда каждый бит криптограмм зависит от каждого бита исходного сообщения.

По схеме Фейстельа построены следующие шифры: DES, ГОСТ,COST,CAST,Blowfish,Safer,FEAL,REDOC,LOKI,RC2,IDEA,MMB,SKIPJACKи другие.

Требования: простота реализации, скорость реализации.

На практике в качестве базисных операция используются:

 - mod2, -mod2³², >> - технический сдвиг вправо, << - технический сдвиг влево, таблицы замен (подстановок), перестановки.

Орбиты при n=2

x₇ (x1,x2)

x₄ (x2,x3) паутинная

x_5x6 (x3,x4) диаграмма

x₂ (x4,x5) орбиты

x₁ (x5,x6)

x₃ (x6, x7)

_x6

x₃ x₁ x₂ x₅x₄x₇

Если длина орбиты короткая, то криптостойкость маленькая. Если она замкнется, то это значит, что произошла дешифровка.

Лекция №2

1 способ – рекурсивно-инволютивный

2 способ – композиционный

→ → → →…………….→ → → →

конвейерный

L₁ o T₁ o R₁

L₁(T₁) L₁(T₁(R₁))

L_n o T_n o R_n

i: L_i^-1 T_i^-1 R_i^-1 ← ←…← ← ← ←

Рассмотрим возможности программной реализации рекурсивно-инволютивного способа.

число бит

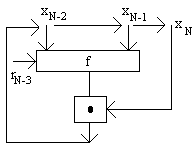
n=3 <x₁,x₂,x₃> ||x₁||₂= ||x₂||₂= ||x₃||₂=m

x₄ = x₁ o f(x₂, x₃, r₁)

x₅ = x₂ o f(x₃, x₄, r₂)

x₆ = x₃ o f(x₄, x₅, r₃)

…………………… N-3 шагов

x_N-2 = r_N-5 o f(x_N-4, x_N-3, r_N-5)

x_N-1=x_N-4 of(x_N-5,x_N-2,x_N-4)

x_N=x_N-3of(x_N-2,x_N-1,r_N-3)

конвейерная

реализация

регистр сдвига “влево”

рекурсивно- инволютивный способ шифрации

на регистрах сдвига с обратной связью

aob=c– прямая операция

a=cb– обратная

сдвиг вправо

обратная шифрация

x_N-3 =f(x_N-2,x_N-1,r_N-3)x_N

K – ключевое пространство.

kK k = <r₁, r₂, …, r_n>

Gⁿ r_iG

Желательно испытывать для генерации ключевой последовательности“хорошие”физические датчики случайных чисел.

^k

r₁,r₂, …,r_n,r_n+1, …,r_N-n– последовательность должна обладать

_k свойствами симметрии.

<r₁,r₂, ...,r_n> =k- исходный ключ

r_n+1 = r₁  φ(r₂, ..., r_n; )

r_n+2 = r₂  φ(r₃, ..., r_n+1; )

Отбор функции f.

o=как правило (побитное суммированиеmod 2)

n=3 детерминированная функция шифрации

n=3 f(x,y,z) = |x r + y|

(1) o=

^{детерминированная функция шифрации}

СХЕМА 11 (тут не разобрать схему было)

f(x, y, z) = (x  r)^y ||x||₂ = ||y||₂ = ||r||₂ = m = 32

a^(y) = α₁^y1α₂^y2 - α_m^ym

, y=1

α^y =

, y=0

_y

α^y α 0 1

0 1 0

1 0 1

x_i  r_i = | x_i +r_i |₂

Недетерминированный случай

Ф (x, y, z)

|x + y + z|₁₆ = i

по iкак по адресу обращаемся в память, где хранятся различные функцииf_o,f₂, ...,f₁₅.

f_i (x, y, z)

x_i,r_i  G

K- пространство ключей

KGⁿ

SGⁿ

E_k- блочный алгоритм шифрации с ключом к множеству криптограмм

E_k E_k(S)  G E_k(S) – множество криптограмм

||S|| = ||E_k(S)|| при заданном ключе

k₁ ≠ k₂ Є K

1)k: E_k(S)S =

2) k₁ ≠ k₂ E_k1(S)E_k2 (S) = 

3) E_k (...E_k (E_k (E_k ( S )))...)

E_k o E_k o ...o E_k (S) o S =  - желательно, чтобы было так

m

Лекция №3

Поточные шифры

ошибка не распростроняется

шифровательная последовательность - гамма

Случайные последовательности

Д. Х. Лемер (1951г.)

Случайная последовательность

последовательность, каждый элементы последовательности

член которой непредсказуем удовлетворяют ряду статис-

для непосвященного тических критериев (тестов)

в известной степени зависящих

того, для каких применений

служит эта последовательность

Дж. И. Фрэнкмен (1962г.)

Случайная последовательность

последовательность, обладающая последовательность независи-

любым свойством, которым обла- мых и одинаково распростра-

дает бесконечная последователь- ненных по равномерному

ность независимых выборок закону случайных величин

случайных переменных из

равномерного распределения

Идеальный генератор случайной последовательности (бинарной) - G- последовательность случайных бинарных величин₁,₂, ...,_n, ..., где_iстатистически независимы и одинаково распределены.

1,p= 1/2 (вероятность)

_i=

0, p = 1/2

x_n+1 = |ax_n+c|_m- конгруэнтная последовательность (Кнут, "Искусство программирования", т. 2)

Хорошие конгруэнтные последовательности по Кнуту должны удовлетворять условиям:

1) x_oZ_n

2) m– произвольное, еслиm= 2^S,S- разрядность компьютера, то |a|₈=S

3)

4) c- нечетное, еслиm= 2^S

Пример:a= 9301,m= 233280,c= 49297

Доказали, что конгруэнтные последовательности предсказуемы:

x_n+1 = | a₁x² + a₂x = a₃ |_m

x_n+1 = | a₁x³ + a₂x² + a₃x + a₄ |_m

Необходимый материал для анализа случайной последовательности:

- тестирование последовательности на случайность;

- эффективные генераторы случайной последовательности над конечным полем;

- случайность и хаос.

Стойкость методов шифрования считается слабой, если генерируемые ими шифрограммы оказываются неслучайными.

Статистические тесты

1. Пусть задан идеальный генератор бинарных случайных последовательностей; нужно получить с помощью этого генератора следующую величину , которая принимает значения: 0, 1, 2, ...,nс равной вероятностью 1/(n+1).

 - идеальный генератор. 0 < 1

 = 0, ₁,₂, ... все_i- независимые случайные величины с вероятностным распределением

1, ????

_i=

0, ????

=>  - равномерно распределена на[0,1)

Рассмотрим случайную величину:

0<n+1

N

k: (0kn+1)N

p(=k)

=k <=> k(n+1)<k+1 <=> =>

Итак, p(=k)=.

Практический вопрос: до каких пор генератор  (т.е. _i)

или: сколько тактов генерируется случайная величина _i нужно нашему генератору, чтобы точно вычислить значения  = 0, ₁, ₂, ...

=> ,

Для того, чтобы точно вычислить сл. велич. достаточноS+1бит сл. велич. 2^S(n+1)<2^S+1.

Лекция №4

Статистические тесты.

G_o – идеальный генератор случайных бит

G_o: ₁, ₂, … , _N

1, p=1/2

i: _i=

0, p=1/2

Опр. Генератор псевдослучайных бит - _o

_o:S₁, S₂, … , S_N

если он статически эквивалентенидеальному генератору G₀, т.е. _oG_o.

- комплекс тестов

Статистический тест: задан идеальный генератор G_o

NN

множество последовательностей

1 0

Функция _т: {“принять”, “отвергнуть”}

U_N - множество всех отвергнутых последовательностей.

|U_N| - количество элементов множестваU_N.

Для идеальных последовательностей: U_N=.

~0.010.001 (на практике)

вероятность

если мало, то последняя последовательность для :_o: {1;0}

если(0,001;0,01), то говорят, что _oG_o.

стат

Обычно не удается оценить |U_N|; переходят к использованию статистик.

Статистика – некоторая функцияf_т (U₁, … ,U_N): P(f_т(U₁, … ,U_N)<) легко оценивается (обычно эта вероятность оценивается нормальным знаком,

-квадрат, … )

(x₁,x₂) – доверительный интервал

=P(f_т < x₁) + P(f_т > x₂) : =(0.001;0.01)

Задан псевдослучайный генератор _{o .}

P(f_т < x₁) + P(f_т > x₂)=, если(0.001;0.01) => псевдогенератор прошел через заданный тест.

• Статистический генератор (конгруэнтный)

x_i+1=|ax_i+b|_Д

0x_i<Д

уметь выделять или составлять битовые последовательности из данных генератора

1) Д<N

m раз снять результаты генератора и составить последовательность

S₁,S₂,…,S_N

2) Д>N,

• Построение гистограмм

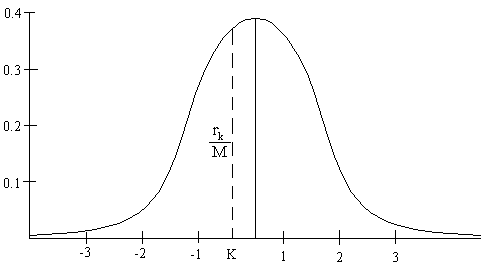
G_o – идеальный датчик

пусть - случайная величина (нормированная)

нормально распределенная

матем.одидание=0, дисперсия=1

	0.1	0.05	0.025	0.010	0.005	0.0025	0.001	0.0005
x	1.2816	1.6449	1.9600	2.3263	2.5758	2.8070	3.002	3.2005

- разбивается на 100 частей

100 ячеек памяти

№ ячейки – номер интервала

M=100*10 – количество экспериментов

R_k – число попаданий в каждую ячейку

- нормир. попаданий

Частотный тест

G_o – идеальный генераторN: <₁,…, _N>

_i – независимая, один. распределенная случайная величина

= (K – число единиц) =

Нормирование сл.

рассмотрим величину: (*)

Теорема Муавра-Лапласа

приN =>

нормальное распределение с M=0, Д=1

• можем взять за статистику функцию (*)

Пусть дан псевдослучайный генератор бит _o

N=500, 1000, 2000

h – шаг гистограммы =6/100=0.06

число экспериментов M (обращение к генератору _o для формирования

N-битной последовательности)

M=10*100

шагов

Далее строим гистограмму

Лекция №5

Корреляционный тест

_o: => =<S₁, S₂, … , S_N>

Существует корреляция между i-ым битом иi+ битом,- сдвиг, фиксированный.

Решение: 1)

2) в М экспериментах подверг. частотному тесту.

Смысл: Н_о (гипотеза) – корреляций нет;

Н₁– корреляция есть.

Н_о => если последовательности наблюдений{} удовлетворяют частному критерию, то верноH_o (результат тем более точнее, чем большеN).

Тест, основанный на критерии -квадрат с (-1) степенями свободы.

Сл. величина независимо распределенных по нормиров. нормальному закону имеет функция плотности вероятности.

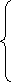
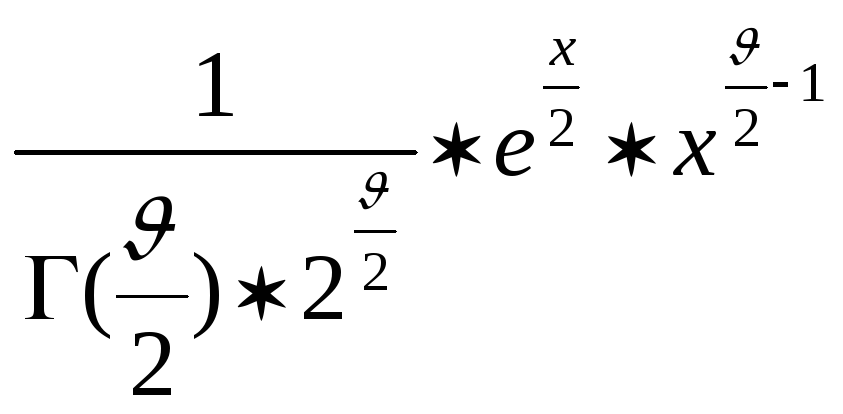, x>0

P(x)=

0 , x<0

(x) – функция Эйлера Г(x)=

= - медиана

=2- дисперсия

-1=7, L=3

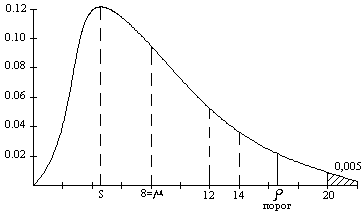
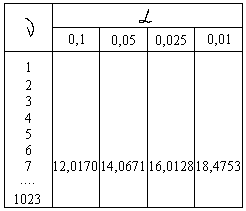
P(>12,0170)=0,1 P(>16,0128)=0,025

P(>14,0671)=0,05 P(>18,4753)=0,01

P(>20,2777)=0,005 P(>24,3219)=0,001

Тест последовательный

L– параметр

_o: => =<S₁, S₂, … , S_N> , N=mL

т.е. строка N-бит разбивается на блоки длиныL

Внашем экспериментеL=8

n_i( ) – число, заключенное в интервал 0x???????????????????????????????

N, тоf_T² с (2-1) степенью свободы

P(n_i=r)=, 0r

=> содержащийm-байт, описывает результат т-испыт по сходимости Бернули

q=P(n_ir)=1-

M(n_i)=m

Д(n_i)=

при большихL

=P(>k)

Замечание (из опыта): требуется, чтобы

L=3 N5*2³*3=120

L=8 N5*256*8=10240

Алгоритмическое построение линейного генератора.

Как построить линейный генератор последовательностей над полем GF(qⁿ) максимального периода?

Дано поле GF(qⁿ)

f(x) - примитивный полином степениn-1 над полемGF(qⁿ):

f(x) не имеет корней в полеGF(q)

GF(qⁿ) – корень полиномаf(n), степени которого порождают мультипликативную группуGF^(qⁿ) поляGF(qⁿ);

По умолчанию мы переходим от сравнений к равенствам. Например, означает, что многочлен(x)=  GF(qⁿ).

(mod (f(x))

x  GF(qⁿ): x=₁₁+₂₂+…+_n_n

<₁,…,_n> - базис,_iGF(q)

GF(qⁿ) – линейное пространство размерностиn над полемGF(q)

1^аязадача: показать, что существует базис векторов₁, ₂,…, _n такой, что каждая степеньⁱ представляется линейной комбинацией векторов₁, ₂,…, _n таких, что компоненты разложенияⁱ по этому базису представляется линейной функцией от степеней (^m+i).

Опр.:пустьGF(qⁿ); следомэлементаназывается величина .

Свойства функции S():

1^o: GF^*(qⁿ) : S()GF(q)

Док-во: возведем в степень q величинуS()

согласно преобразованию Фробенпуса такое равенство возможно  S()GF(q).

Лекция №6

Конечное поле GF(qⁿ).

f(x)=xⁿ+f₁x^n-1+f₂x^n-2+…+f_n примитивный неприводимый полином надGF(q).

f()=0,  -примитивный элемент поляGF(qⁿ)

степени ⁱ порождают элементыGF^*(qⁿ).

GF(qⁿ):

- след элемента.

Свойства: S(): S: GF(qⁿ)->GF(qⁿ)

1. S(GF(q)

2. ,GF(qⁿ) : S(+)=S()+S() – линейность

Д-во: S(+)=.

3. cGF(q) : S(c)=cS() - однородность

Д-во: S(c)=

i,m N (S(^i+m))0 Показать, что эта последовательность имеет периодqⁿ-1.

S(^m), S(^1+m), S(^2+m),…,

=>

qⁿ-1=T , покажем, что это минимальный период.

<S(^m+i), S(^m+i+1),…, S(^m+i+n-1)>

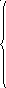S(^m+i)=

^{…………………………………………………………………………………………………}

= *

……… ……………………………. ……

1 1 1 ….1

det A=….

……………………………

….

1 1 1 ….. 1

…..

W(x₁, x₂,…, x_n)= …..=определитель

….. Вандермонда

-порожд. элемент

₁ ₂ … _n

=>A – невырожденная => A^-1= ………………

………………

₁ ₂ … _n S(^m+i)

……………… S(^m+i+1)

……………… ……….. = ……

……………… S(^m+i+n-1)

ⁱ =S(^m+i)₁+ S(^m+i+1) ₂+…+ S(^m+i+n-1) _n, i,m

i=0,1,…,(qⁿ-2);  пробегает все ненулевые элементы поляGF(qⁿ) =>

линейные координаты =>

1. система векторов <₁, ₂,…,_n> образует базис в линейном пространствеGF(qⁿ);

2. при ij _i_j то всеn-гаммы последовательности (S(^i+m))различны;

3. последовательность (S(^i+m))_i имеет истинный период T=qⁿ-1;

Покажем, что такая последовательность порождается с помощью примитивного полинома f(x)=xⁿ+f₁x^n-1+…+f_n

x= - примитивный элементf()=0

ⁿ+f₁^n-1+…+f_n=0

^n+m+i=-f₁^m+i+n-1-…-f_n^m+i

S(^n+m+i)=-f₁S(^m+i+n-1)-…-f_nS(^m+i)

S(^m+n+i)=S_m+n+i-1 (обозначим)

S_m+n+i=-f₁ S_m+n+i-1-…- f_n S_m+i

Все элементы последовательности S(^i+m) порождается рекурсивной формулой.

Лекция №7

Обзор предыдущего.

 функция след, определенная на GF(qⁿ) формулой:GF(qⁿ)

отображает GF(qⁿ) наGF(q).

 функция след S() является линейной формулой, т.е.a₁,a₂GF(q)

S(a₁₁+a₂₂)=a₁S(₁)+a₂S(₂)

 если - корень примитивного полинома надGF(q)

f(x)=xⁿ+f₁x^n-1+f₂x^n-2+…+f₀ порождающего полеGF(qⁿ), тоi,mN базис в линейном пространствеGF(qⁿ) : ₁,₂,…, _n такой что

^i+m=S(^i+m) ₁+ S(^i+m+1) ₂+…+ S(^i+m+n-1) _n, m.

Иными словами, элемент ^i+mGF(qⁿ) единственным образом характеризуетсяn-граммой(S(^i+m), S(^i+m+1),…, S(^i+m+n-1)).

Все n-граммы последовательности (S(^i+m))_i0 m – различны => m последовательность (S(^i+m))_i0 имеет минимальный периодT=qⁿ-1.

Покажем, что последовательность (S(^i+m))_i0 m порождается линейной рекурсивной формулой.

Дано: f()=0;

ⁿ+f₁^n-1+f₂^n-2+…+f_n=0

^i+m+n=-f₁^i+m+n-1-f₂^i+m+n-2-…-f_n^i+m

применим ф-ию – след. и воспользуемся свойством линейности: обозначим

b_i=-f_i;

S(^i+m+n)=b₁S(^i+m+n-1)+b₂S(^i+m+n-2)+…+b_nS(^i+m), i,mN.

S_k=S(^k) – обозначение.

S_i+m+n=b₁S_i+m+n-1+b₂ S_i+m+n-2+…+b_n S_i+m

 <S₁, S₂,…, S_n> - начальнаяn-грамма

S_n+1=b₁S_n+ b₂S_n-1+…+ b_nS₁

S_n+2=b₁S_n+1+ b₂S_n+…+ b_nS₂

……………………………

f(x)=xⁿ+f₁x^n-1+…+f_n – характеристический полином последовательности (должен быть примитивным);

каждая интерполяция: n – умножений,(n-1) – сложений в полеGF(q).

Для программной реализации (на машине с регистром 2³²)q-простое порядка 2¹⁶.

Схематическое представление:

регистр сдвига с

функцией обратной

связи

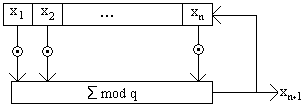
регистр сдвига с

линейной обратной

связью - РСЛОС

q=2:

Некоторые полиномы над GF(2):

(1,0)=x+1 (7,3,0)

(2,1,0) (7,4,3,2)

(3,1,0) (9,4,0)

(4,1,0) (10,3,0)

(5,2,0) (11,2,0)

(6,1,0) (12,6,9,1,0)

(7,1,0) (13,4,3,1,0)

(14,5,3,1,0) (18,5,2,1,0) (24,3,1,0)

(15,1,0) (19,5,2,1,0)

(16,5,3,2,0) (20,3,0) (32,7,6,2,0)

(17,3,0) (21,2,0) (32,7,5,3,2,1,0)

(17,5,0) (22,1,0)

(17,7,0) (23,5,0)

y(x₁, x₂,…, x_n)=( фиксированнаяn-грамма (r₁, r₂,…, r_n) )

четность (нечетность) числа совпавших символов (x=r).

1, x=r

X^r=

0, xr

x^r:=x~r

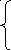Задача: исследовать на равномерную распределенность.

……………………………………

1. Метод комбинаторный.

2. Метод фильтрации.

1: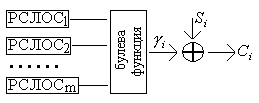

i-й такт.

f(u₁,…, u_m)=

2:

исходное сообщение: <x₀, x₁,…, x_n>

исходный ключ: <r₁,…,r_n>  РСЛОС

………………………………

Лекция №8

Защита информации в связи.

Итерационный подход.

Шеннон:

^{(Хилл 1926) (невырожд. det0)}

A – матрицаnn неособая, элементы матрицы = ключевой материал;

- шум (ключевой вектор)

- в-р сообщение



- n штук, линейно независ. (чтобы однозначно восстановить матрицу А)

_k

-k=1,2,…,n

b₁=(1,0,…,0)

a₁₁ a₁₂ … a_1n

A= a₂₁ a₂₂ … a_2n

……………….

a_n1 a_n2 … a_nn

=> не выдерживает атаки 3-го уровня => для этого необходимо менять элементы матрицы А, или вектор .

t – сеансный параметр

- система блуждающих ключей

Но при этом матрица А должна оставаться обратимой.

Элементы теории самокорректирующихся кодов.

Теория интерполирования над полем F.

<g_0,g₁,…,g_n-1> - система функций надF со значениями вF, линейно независима.

Задача интерполирования (в частной постановке):

• заданы точки x_o,x₁,…,x_k-2,x_k-1 – различные элементы изF (фиксиров.);

• заданы значения функции f(x) в этих точкахf(x₀),f(x₁),…,f(x_k-1) ( y_i=f(x_i) )

требуется построить линейную комбинацию g_i(x), i=0-(k-1) : такую, что(j=0,…,k-1).

Т.к. линейно независимы, то определитель

g₀(x₀) g₁(x₀) … g_k-1(x₀)

Д(x₀,x₁,…,x_k-1)= g₀(x₁) g₁(x₁) … g_k-1(x₁) 0

……………………………

g₀(x_k-1) g₁(x_k-1) … g_k-1(x_k-1)

=> задача интерполирования поставлена корректно, т.е. имеет единственное решение.

Опр.Система функций называется чебышевской (с – системой), если определитель Д0 для любого выбора элементовx₀,x₁,…,x_k-1 изF.

Задача (в общей постановке):

задан произвольный набор точекx₁,x₂,…,x_k-1 изF

и т.д. …

постановка корректна, если система базисных функций из F является с-системой.

• (k-1) < |F|

• x₁F, k-1||<|F|, c-система задается на

Возможны ограничения.

Когда система функций называется чебышевской?

Теорема: для того, чтобы системабыла чебышевской необходимо и достаточно, чтобы любая нетривиальная линейная комбинация этих функций имела не более чемn корней, иными словамиa₀,a₁,…,a_n-1 функцияимеет меньше, чемn корней (число корнейn-1).

Доказательство: пусть существуетk корней:₀,₁,…,_k-1 F

(1), 0jk-1, но- является с-системой ₀,₁,…,_k-1

Д(₀,₁,…,_k-1)0

Если - c-система из (1) следует, чтоa_i=a₁=…=a_k-1=0.

Опр.:C-система являетсямарковскойсистемой, если любое подмножество этих функций является с-системой.

Решение задачи интерполяции в общей постановке.

Пусть задана произвольная последовательность различных точек (узлов, локаторов): x₀,x₁,…,x_k-1 из поляF.

Система функций -марковская.

Задано: значения y₀,y₁,…,y_k-1 функцийg(x) в узлахx₀,x₁,…,x_k-1, требуется построить функцию(x): (x)=такую, что(x_j)=y_j, j=0,…,k-1;

Для решения рассмотрим систему:

a₀g₀(x₀)+ a₁g₁(x₀)+…+ a_k-1g_k-1(x₀)-y₀=0

a₀g₀(x₁)+ a₁g₁(x₁)+…+ a_k-1g_k-1(x₁)-y₁=0

………………………………………..

a₀g₀(x_k-1)+ a₁g₁(x_k-1)+…+ a_k-1g_k-1(x_k-1)-y_k-1=0

a₀g₀(x)+ a₁g₁(x)+…+ a_k-1g_k-1(x)-(x)=0

составим определитель:

g₀(x₀) g₁(x₀) … g_k-1(x₀) y₀

g₀(x₁) g₁(x₁) … g_k-1(x₁) y₁

……………………………………

g₀(x_k-1) g₁(x_k-1) … g_k-1(x_k-1) y_k-1

g₀(x) g₁(x) … g_k-1(x) (x)

этот определитель будем разлагать по элементам последнего столбца:

g₀(x₀) g₁(x₀) … g_k-1(x₀)

g₀(x₁) g₁(x₁) … g_k-1(x₁) g₀(x₂) g₁(x₂) … g_k-1(x₂)

……………………………….  y₀ + (-1)y₁ ……………………………. +…+

g₀(x_k-1) g₁(x_k-1) … g_k-1(x_k-1) g₀(x_k-1) g₁(x_k-1) … g_k-1(x_k-1)

g₀(x) g₁(x) … g_k-1(x) g₀(x) g₁(x) … g_k-1(x)

+(-1)^k(x)Д(x₀,x₁,…,x_k-1)=0.

Лекция №9

F: F

x₀,x₁,…,x_n-1

g₀(x),g₁(x),…,g_n-1(x)

C-система на: любая нетривиальная линейная комбинация этих функций не более чемn-1 различных корней.

Марковская система – чебышевская система g₀,g₁,…,g_n-1, гдеподмножествоg₀,g₁,…,g_i-1 является с-системой (м-система).

П: 1,x,x²,…,x^n-1 – c-система

, a_kF – имеет не более (n-1) корней – является и м-системой.

Пусть ₀(x), ₁(x),…,_n-1(x) – функции, не имеющие корней на множествеF, n=|x||F|, тогда функции₀(x), x₁(x),x²₂(x),…,x^n-1_n-1(x) – тоже являются

м-системой.174

Задача интерполирования в общей постановке.

Заданы значения: y_k=f(x_k), k=0,…,n;

в n различных узлах (локаторах) x₀,x₁,…,x_n-1 требуется найти такие(a_iF), чтотакова:(x)=y_k, 0kn-1

Система уровнений:

a₀g₀(x₀)+ a₁g₁(x₀)+…+ a_n-1g_n-1(x₀)-y₀=0

a₀g₀(x₁)+ a₁g₁(x₁)+…+ a_n-1g_n-1(x₁)-y₁=0

………………………………………..

a₀g₀(x_n-1)+ a₁g₁(x_n-1)+…+ a_n-1g_n-1(x_n-1)-y_n-1=0

a₀g₀(x)+ a₁g₁(x)+…+ a_n-1g_n-1(x)-(x)=0

Определитель:

g₀(x₀) g₁(x₀) … g_n-1(x₀) y₀

g₀(x₁) g₁(x₁) … g_n-1(x₁) y₁

…………………………………… =0

g₀(x_n-1) g₁(x_n-1) … g_n-1(x_n-1) y_n-1

g₀(x) g₁(x) … g_n-1(x) (x) (нетривиальные решения)

Разложим по элементам последнего столбца:

g₀(x₀) g₁(x₀) … g_n-1(x₀)

g₀(x₁) g₁(x₁) … g_n-1(x₁) g₀(x₂) g₁(x₂) … g_n-1(x₂)

……………………………….  y₀ + (-1)y₁ ……………………………. +

g₀(x_n-1) g₁(x_n-1) … g_n-1(x_n-1) g₀(x_n-1) g₁(x_n-1) … g_n-1(x_n-1)

g₀(x) g₁(x) … g_n-1(x) g₀(x) g₁(x) … g_n-1(x)

g₀(x₀) g₁(x₀) … g_n-1(x₀)

g₀(x₂) g₁(x₂) … g_n-1(x₂)

+ (-1)²y₂ ……………………………. +…+ (-1)ⁿ(x)Д(x₀,x₁,…,x_n-1)= 0 =

g₀(x_n-1) g₁(x_n-1) … g_n-1(x_n-1)

g₀(x) g₁(x) … g_n-1(x)

g₀(x) g₁(x) … g_n-1(x) g₀(x₀) g₁(x₀) … g_n-1(x₀)

(-1)^n-1y₀ g₀(x₁) g₁(x₁) … g_n-1(x₁) =(-1)^n-1y₁ g₀(x) g₁(x) … g_n-1(x)

.…………………………… ……………………………..

g₀(x_n-1) g₁(x_n-1) … g_n-1(x_n-1) g₀(x_n-1) g₁(x_n-1) … g_n-1(x_n-1)

g₀(x₀) g₁(x₀) … g_n-1(x₀)

g₀(x₂) g₁(x₂) … g_n-1(x₂)

+ (-1)^n-1y₂ ……………………………. +…+ (-1)ⁿ(x)Д(x₀,x₁,…,x_n-1) = 0.

g₀(x_n-1) g₁(x_n-1) … g_n-1(x_n-1)

g₀(x) g₁(x) … g_n-1(x)

Обозначим Д(x,x₁,x₂,…,x_n-1) - 1^ыйопределитель,

Д(x₀,x,x₂,…,x_n-1) - 2^ойопределитель,

Д(x₀,x₁,x,…,x_n-1) - 3^ийопределитель,

……………………………………..

(x)=⁽¹⁾, гдеB_i(x)=(2)

0, ij (в определителе будет 2 одинаковых строки)

B_i(x_j)=

1,i=j

x_i=x_k (x_k)=y_k

k,i = n-1

Разложим функции B_i(x) в базисе:

(3)

{0kn-1

{0in-1

Элементы теории самокорректирующихся кодов.

Общие принципы:

Дан канал связи:

С источником ошибки :

Множество сообщений: S

S S’

^{вх.сообщ. вых.сообщ.}

А – алфавит S=(s₁,s₂,…,s_n) – блок длиныnв алфавитеA

Канал характеризуется типом ошибок Т

• ошибки независимые

• ошибка налагается на i-ю позицию сообщения и переводит её:S_i’(S_i+l_i)

Код называется самокорректирующимся:

SS _cod

T S S

^decod

decod(cod S + )=S

Типы ошибок.

 aA a  a’ (a’A) 1 род (ошибка замены)

 aA a   (пустой символ) 2 род (ошибка стирания)

 aA   a 3 род (ошибка вставки)

Фиксируется:

• длина блока (n)

• тип Т ошибки

T=<t₁,t₂,t₃>

t₁ – число возможгых ошибок 1^города на блоке длиныn

t₂ – 2 рода

t₃ – 3 рода

Лекция №10

A={,a₁,…,a_m}

A^*=

A_n={z|z=(x₁,…,x_n), x_iA, 1in}

A₀={}

SA^*, S – множество сообщений

S S’

T=<t₁,t₂,t₃>

C-кодовые слова

Множество С называется кодом, если выполняются следующие условия:

1. ошибки вносятся из класса Т

2. трансформацию за счет внесения ошибок обозначим: , tT

Понятие “наложение” ошибки:

S=(a₁,a₂,…,a_n)

S’_t – отлично отS в не более, чемt символах, т.е.S’_t получаеся заменой символов в позициях не более чемt на новые символы.

3. Множесво T(s):={S’C|S’=S’t, где } т.е.T(S) – множество

всевозможных слов из С, которые получаюся из слова S посредством всех возможных ошибок типа Т (tT). T(S) называется окрестностью ошибок типа Т.

Должно выполняться следущее условие:

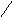
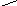
S₁S₂  C: T(S₁)T(S₂)=

S₂

S₁

T(S₁) T(S₂)

Эти условия гарантируют, что код С является самокорректирующимсяна ошибках типа Т.

На множестве А_n может быть введена метрика Хэмминга:

x₁,x₂A_n (x₁,x₂)=

x₁=(x₁₁, x₂₁,…, x_n1)

x₂=(x₁₂, x₂₂,…, x_n2)

1, x_k1x_k2

(x_k1+x_k2)=

0, x_k1=x_k2

число символов, в которых отличаются слова x₁ и x₂

Рассмотрим Хэмминга, удовлетворяющего метрике.

xA_n (x,x)=0 - рефлексивность

x,yA_n (x,y)=(y,x) - симметричность

x,y,zA_n (x,y)<(x,z)+(z,y) - акс.

Как свойство самокоррекции может быть выражено в терминах метрики Хэмминга.

Дан код С:

Опр.Кодовым расстоянием кода С называется числоd(C)=min (x,y), xy.

Код С является самокорректирующимся кодом обнаруживающим и исправляющим любую ошибку кратности tT, если выполняется увловие:

x,yC xy (x,y)2t+1 ( d(C)2t+1 )

Всякая ошибка e_t кратностиt (tT) внесенная в словоxC дает словоx’_t, которое отличается от x вt позициях, т.е.( x’_t,x)t

yC по условию(x,y)2t+1 (yx)

2t+1(x,y)(x, x’_t)+( x’_t,y)t+( x’_t,y)

(x’_t,y)t+1 yx

(x,x’_t)t

T(x)={x’_t|(x,x’_t)t}

^{t окрестность слова х}

t

(x,y)2t+1 не пересекаются

( x’_t,y)t+1 x y => самокор.

Наложить дополнительную алгебраическую структуру на A_n. Будем считать, чтоA=Fq – поле порядкаq.

A_n – слова длиныn изF (линейное пространство).

Логарифмическая мощность кода С.

Скорость кода.

- скорость передачи

d=d(l)=min (x,y), x,yC,xy

- относительное кодовое расстояние

d(C)2t+1 => C – самокор. обнаружено и исправленоtошибок типаT.

C код называется[n,k,d] – код.

Линейные коды.

Код СF называется линейным, если множество С является К-мерным подмножествомn-мерного пространстваF.

Логарифмическая мощность кода С в этом случае характеризуется размерностью подпространства С.

Различаются 2 случая характеризации линейного кода С.

1_случай: рассмотрим линейное отображение

: FF

В этой ситуации код С есть образ F при отображении . Матрица этого отображения называется порождающей матрицей.

2_случай: рассмотрим линейное отображение

: FF

В этой ситуации код С является ядром отображения  (ядро линейных отображений есть множество всех векторов, которые отображаются в нулевой вектор). В этом случае матрица отображения и называется проверочной.

Лекция №11