Примеры решения задач по первой части теоретического блока

1.1. Расчет простейших электрических цепей с помощью законов Ома и Джоуля-Ленца.

1.* Дано:

Рассчитать все токи в цепи и определить мощность, рассеиваемую на каждом резисторе.

Решение:

Эквивалентное сопротивление цепи с учетом того, что R₁ и R₄ соединены последовательно, а R₂ и R₃ параллельно, равно

;

Токи I₁ и I₄ находятся по закону Ома

.

Напряжение на резисторах R₂ и R₃ будет равно

;

Токи I₂ и I₃ находим также по закону Ома

;

.

Мощность, рассеиваемая в резисторах:

Мощность источника:

Суммарная мощность приемников после суммирования P₁, P₂ и т.д. оказывается, также равна 24,8 Вт. В этом случае говорят, что сходится баланс мощности в цепи. Последнее означает отсутствие ошибок при расчете токов.

2.* Три одинаковых резистора соединены по смешанной схеме (два в параллель и один последовательно) и потребляют от источника мощность P=100 Вт.

Определить мощность, которую будут потреблять эти резисторы от источника при параллельном и последовательном включении.

Решение:

Считая сопротивление одного резистора, равным R, общее сопротивление цепи при смешанном включении будет равно

При последовательном соединении резисторов сопротивление цепи будет равно

Так при этом ,считая напряжение источника неизменным, общее сопротивление уменьшается в 2 раза.

Мощность пропорциональна квадрату тока и первой степени сопротивления. (P=I²r)

Это означает, что при уменьшении тока в 2 раза и возрастании сопротивления цепи в 2 раза мощность в 2 раза уменьшится и составит 50 Вт.

При параллельном соединении трех резисторов сопротивление цепи составит

То есть, будет в 3 раза меньше, чем при смешанном соединении. Соответственно ток возрастет в 3 раза, и мощность тоже увеличится в 3 раза и составит 300 Вт.

3 .* Дано: R₁=5 Ом; R₂=R₃=10 Ом; R₄=5 Ом; R₅=10 Ом; U=20 В. Рассчитать все токи в цепи (рис. 2) методом пропорционального пересчета.

Решение:

Задаемся током в R₂: I₂’=1 А.

В этом случае напряжение на R₂ и R₃ (они включены параллельно) будет равно

Ток в R₃:

Ток может быть найден по 1-му закону Кирхгофа

Напряжение на R₅:

Ток

По 1-му закону Кирхгофа:

Напряжение на зажимах цепи:

Сравниваем полученное значение напряжения с заданным и определяем коэффициент пересчета

Теперь определяем действительные значения токов в цепи

и т.д.

1.2. Преобразование схем электрических цепей

4.* Три одинаковых источника с E=6B и внутренним сопротивлением r=3Ом включены в параллель и работают на общую нагрузку, сопротивление которой равно R. При каком сопротивлении нагрузки в нем выделяется максимально возможная мощность?

Решение:

В заданной схеме (рис. 3) целесообразно произвести перенос источника за узел. Для этого подключают к узлу источники с ЭДС, равной E, но направленной против ЭДС заданных источников.

Преобразование ясно из рис. 4,а и 4,б.

a) б)

Рис. 4.

Максимально возможная мощность выделится в нагрузке, если ее сопротивление равно внутреннему сопротивлению источника (режим согласованной нагрузки).

Внутреннее сопротивление источника оказывается равным . Откуда

Мощность в нагрузке составит

5.* Дано: E₁=6B; E₂=4B; R1=2Ом; R₂=R₃=6Ом; R₄=4Ом; R₅=1Ом.

Рассчитать токи источников в цепи (рис. 5)

Решение:

Схему целесообразно представить в виде рис.6, используя преобразование треугольника сопротивлений в эквивалентную звезду.

При этом

R₅

Схему рис. 6 можно представить, как это показано на рис. 7, и рассчитывать ее методом наложения

Закорачиваем второй источник и находим ток первого

Ток в сопротивлении при этом будет равен

Далее закорачиваем первый источник и находим ток второго

Ток в сопротивлении при действии в цепи только второго источника находим по формуле:

В соответствии с направлениями токов, показанными на рис. 7 находим действительные значения токов источников.

6.* Дано:E₂=2B;E₄=4B;R₁=2Ом; R₂=1Ом; R₃=1,5Ом; R₄=1Ом; R₅=1,6Ом; R₆=1,2Ом.

Рассчитать все токи в цепи (рис. 8), составить баланс мощности.

Решение:

Схема цепи имеет три контура и четыре узла и расчет ее с помощью законов Кирхгофа потребует решения шести уравнений.

Однако если преобразовать участки цепи, изображенные на рис. 9 и представляющие собой активные двухполюсники, то трудоемкость расчета существенно снижается.

ЭДС и , сопротивления и можно определить следующим образом:

В результате такого преобразования схема цепи существенно упрощается (рис. 10)

В полученной схеме токи I₃ и I₆ одинаковы и равны

Напряжение между 3-м и 2-м узлами исходной схемы равно

Ток I₅ отсюда

Ток I₄ может быть определен по закону Ома

Напряжение между 1-м и 4-м узлами будет равно

Токи I₁ и I₂ соответственно равны

Составим баланс мощности в цепи.

Мощность, вырабатываемая источниками:

Мощность, потребляемая приемниками:

Таким образом, баланс мощностей в цепи сошелся.

1.3. Анализ сложных электрических цепей постоянного тока. Топология электрических цепей.

7.* Для схемы цепи (рис. 11) вычертить граф, выделить дерево графа, записать матрицы соединений (узловая матрица) и контуров и, используя эти матрицы, получить систему уравнений, записанную по законам Кирхгофа.

a) б)

Рис. 11

Граф данной электрической цепи изображен на рис. 11,б. При этом дерево графа выделено жирными линиями.

Так как деревом графа называют совокупность ветвей, соединяющих все узлы схемы, но не образующей замкнутых контуров, то, очевидно, дерево, приведенное на рис. 11,б, не является единственно возможным.

Студентам предлагается самостоятельно изобразить варианты других деревьев для данного графа.

Матрица соединений (узлов) будет иметь вид:

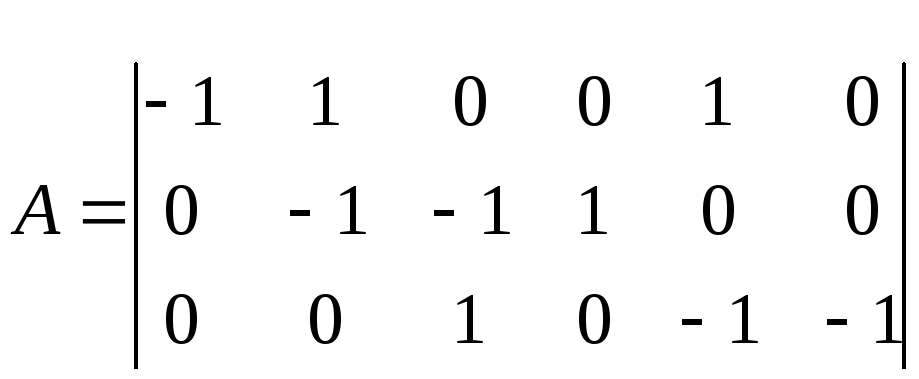, где номера строк – узлы, а номера столбцов – ветви.

Эта матрица записывается для k-1 узлов и, очевидно, поэтому тоже не является единственно возможной. Запишите матрицу А, если исключен, например, 1-й узел либо 2-й.

Задав направление обхода контуров по часовой стрелке (рис. 11,б), записываем матрицу контуров

, где номера строк – контуры, а номера столбцов – ветви.

Для записи уравнений по закону Кирхгофа требуется еще диагональная матрица сопротивлений цепи:

Умножая матрицу соединений на вектор-матрицу токов ветви, имеем

Или

Это уравнения, записанные по 1-му закону Кирхгофа.

Далее матрицу контуров умножаем на вектор-матрицу напряжений ветвей

Или получаем уравнения:

С учетом того, что

Имеем

Это уравнения, записанные по 2-му закону Кирхгофа.

8.* Для схемы, изображенной на рис. 11,а, записать системы уравнений для расчета цепи методом контурных токов и узловых потенциалов, используя матрицы контуров и соединений.

Решение:

При расчете цепи методом узловых потенциалов используется диагональная матрица проводимости ветвей:

,

где и т.д.

Умножаем матрицу соединений на матрицу проводимостей

Умножаем полученный результат на транспонированную матрицу соединений

В результате получили матрицу узловых проводимостей.

Далее матрицу G^У умножаем на вектор-матрицу потенциалов узлов, а вектор-матрицу токов источников тока ветвей умножаем на матрицу соединений

, (*)

где и .

После указанных выше действий получаем

.

Переносим в правую часть системы уравнений и окончательно записываем:

,

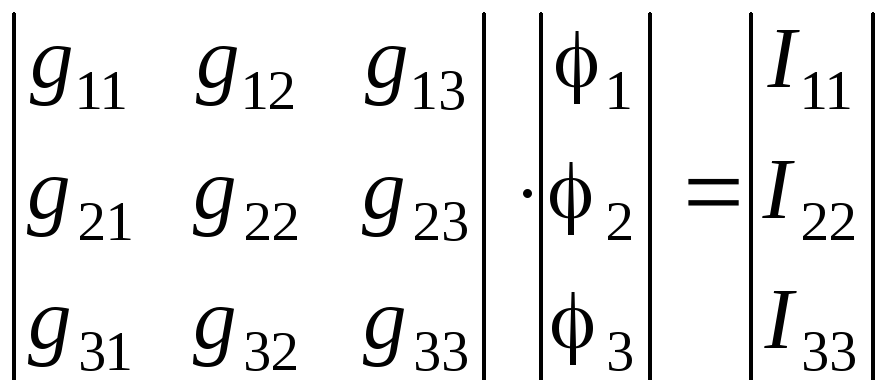где

Для получения системы уравнений в методе контурных токов необходимо матрицу контуров умножить на диагональную матрицу сопротивления ветвей

Полученный результат умножаем на транспонированную матрицу контуров

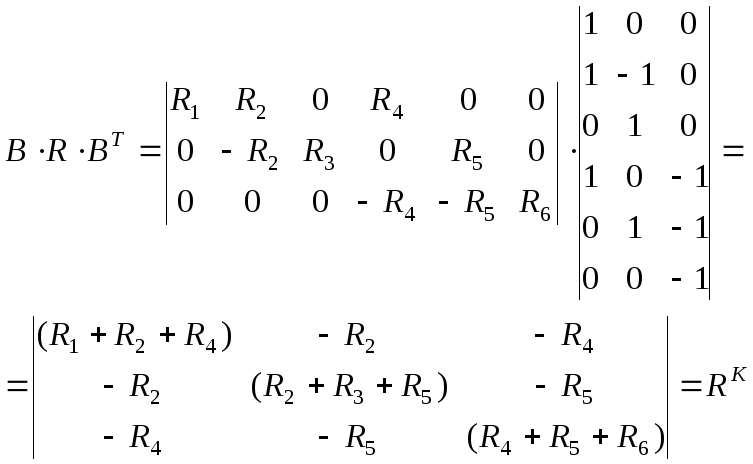
Получили матрицу контурных сопротивлений.

Далее матрицу контуров умножаем на вектор-матрицу ЭДС источников ветвей

.

В результате получили вектор-матрицу контурных ЭДС.

Окончательно имеем

Или

,

где I₁₁, I₂₂, I₃₃ – контурные токи

- контурные сопротивления и сопротивления между контурами

- контурные ЭДС.

1.4. Метод эквивалентного генератора.

9.* Определить показания приборов в схеме представленной на рис.12,а, если: R₁=10Ом; R₂=50Ом; R₃=40Ом; R₄=20Ом; R₅=20Ом.

а)

б)

Рис. 12

Решение: Определяем напряжение холостого хода на зажимах а-б при разомкнутой ветви R₅. При этом токи I₁ и I₂ не будут зависеть друг от друга и могут быть найдены по закону Ома

Напряжение холостого хода будет равно:

Далее находим внутреннее сопротивление активного двухполюсника относительно зажимов а-б при закороченном источнике E. (см. рис. 12,б)

Т ок в сопротивлении R₅ (тот, что регистрирует амперметр)

Показания вольтметра: