Новая папка / Примеры 7

Пример 97. Определить переходную проводимость схемы рис. 8.2.

Решение. При замыкании ключа

По определению, переходная проводимость равна току в цепи при Е=1 В. Следовательно,

Пример 98. Найти собственную переходную проводимость первой ветви g₁₁(t), взаимную переходную проводимость между третьей и первой ветвями g₃₁(t) переходную функцию напряжения на конденса­торе k_uC для схемы рис. 8.34. Параметры схемы: R₁=1000 Ом; R₂=2000 Ом; С=50 мкФ.

Рис. 8.34

Решение. По определению,

С помощью классического метода определим:

Полагая в этих формулах Е=1В, находим:

Подстановка числовых значений дает:

Пример 99. Определить взаимную переходную проводимость между первой и третьей ветвями схемы рис. 8.4, а при включении источника э.д.с. в первую ветвь и следующих значениях параметров:

R1=R2=100 Ом; L1=lГн; C=100мкФ.

Решение. Изображение тока третьей ветви

Корни уравнения М(р)=0 (см. пример 76):

p1= -100+j100; p1= -100-j100;

Полагаем Е=1В и в соответствии с формулой разложения находим

После подстановки значений параметров, корней р1 и р2 и использования формулы получим

Таким образом, взаимная переходная проводимость между третьей и первой ветвями схемы рис. 8.4, а при данных значениях параметров как функция вре­мени представляет собой затухающую синусоиду.

Пример 100. В схеме рис. 8.35;

u(t) = 170sin(314t+30)B; R1=10Ом; R2=5 Ом; R3=15 Ом; L1=30мГ; L2=50 мГ; М=25мГ. Найти i1(t) с помощью формулы разложения.

Рис. 8.35

Решение. Составим уравнения по методу контурных токов:

Совместное их решение дает

Корни уравнения М(р)=0:

Ток

Пример 101. Найти i1=f(t) и u2=f(t) при включении ключа в схеме рис. 8.37, а. Напряжение источника э.д.с. u(f)=100(1-е^-t)В; a=0,25 с-¹; R=0,5 Ом; L1=lГн; М=0,5Гн.

Рис. 8.37

Решение. Переходная проводимость цепи, состоящей из после­довательно включенных R и L,

Первое слагаемое в формуле (8.63) выпадает, так как u(0)=0.

При этом

При интегрировании учитываем, что от  не зависит:

А.

Напряжение на зажимах вторичной обмотки

В.

Пример 102. В электрической цепи рис. 8.37, а в момент времени t=0 замы­кается ключ и напряжение и(t) изменяется в соответствии с рис. 8.37, б; и(0) =50В. В первый интервал времени от t = 0 до t = t1= 4 с напряжение и1 (t) == 150 – 100е, где а ==0,25 c. Во второй интервал времени от t=t1==4 с доt=t2=6 с u2(t)==50+100е, где с==0,4 c. Параметры схемы рис. 8.37, a: R=0,5 Ом; L1=lГ (вторичная цепь разомкнута).

Найти закон изменения тока i1 во времени для обоих интервалов времени, а также значения тока i1 при t==2 и 5 с.

Решение.

g(t)=; b= g(t-)=

В первый интервал времени

i1(t)=u(0)g(t)+ =

При t=2 с

i1 = 100 (1 — е) + 200 (1 + е — 2е) = 94,9 А.

Во второй интервал времени (включая скачок Ub—Ua=36,9 В)

i(t)=и(0)g (t)+ + (Ub - Ua)g(t - tl) + () g {t - ) d

u2(t)=l00ce

i1(t)= 100(1 -e+200(0,632-

-l,718e

При t=5 с

i1(t)=

Пример 103. В качестве иллюстрации методики расчета переходных процес­сов путем введения источника тока найдем для схемы рис. 8. 39, б ток i2 при раз­мыкании ключа третьей ветви, полагая, что до коммутации в схеме был устано­вившийся режим; R1=40 Ом; R2=160 Ом; L=2 Г; E=120 В. После размыка­ния ключа i2=i`2+i``2, где i`2—ток докоммутационного режима; i``2— ток от источ­ника тока I3=0,5 А (в данном случае постоянного) в схеме рис, 8. 39, в (R3=R2).

Изображение тока

Следовательно,

i2=0.5+0.1(1-e)A

Пример 104. На последовательно соединенные R и L поступает серия прямоугольный импульсов напряжения единичной амплитуды;

длительность импульса  и длительность паузы также  (рис. 8.40,е). Используя третий способ в сочетании с теоремой запаздывания (см. § 8.40), находим изображение напряжения:

U(p)=(1-+-+…).

В скобках бесконечная геометрическая прогрессия со знаменате­лем . Сумма членов ее равна . Изображение тока

Применяем формулу разложения. Корни знаменателя: р'=0; p``=-R/L; pk=(ak+jbk) =j(2k+1) (-k).

Группируя член k=0 с k=—1, член k=1 с членом k=—2 и т. д., получим:

Пример 105. Путем использования обобщенных функций решить задачу при­мера 86 (см. рис. 8.24).

Решение. В уравнение для после коммутационной схемы

(a)

подставим: uc1=uc1-(t)1(-t)+uc1+(t)1(t)

uc2=uc2-(t)1(-t)+uc2+(t)1(t)

u`c1=u`c1-(t)1(-t)+u`c1+(t)1(t)+(t)(uc1(0+)–uc1(0-))

u`c2=u`c2-(t)1(-t)+u`c2+(t)1(t)+(t)(uc2(0+)–uc2(0-))

E=E 1(-t)+E 1 (t)

Коэффициенты при 1 (—t), 1 (t) и (t) дают три уравнения:

R(C1u`c1-(t)+C2u`c2-(t))+uc1-(t)=E (б)

R(C1u`c1+(t)+C2u`c2+(t))+uc1+(t)=E (в)

uc1(0+)(C1+C2)=C1uc1(0_)+C2uc2(0_) (г)

Из (б) находим uc1-(t}=E, из (г) uс1 (0+)=C1E/(C1+C2); далее решаем (в)

классическим или операторным методом, имея в виду, что uc1+(t)=Uc2+ (t). В результате получаем тот же ответ, что и в примере 86.

6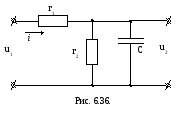.37^*

Для цепи, изображённой на рис. 6.36. записать в общем виде переходные функции по току и напряжению.

Решение: Для расчёта переходных функций цепи по току и напряжению необходимо рассчитать переходный процесс, имеющий место после подключения длинной цепи к источнику постоянного напряжения U₀=1 B;

Используем операторный метод. Входное сопротивление цепи будет равно:

Ток в неразветвлённой части цепи:

Переходим к оригиналу по теореме разложения:

Корни уравнения N(p)=0:

Производная

Подстановка корней в М(р) и

Ток в неразветвлённой части цепи численно будет равен переходной функции по току (переходной проводимости цепи):

Переходную функцию по напряжению можно найти, воспользовавшись вторым законом Кирхгофа:

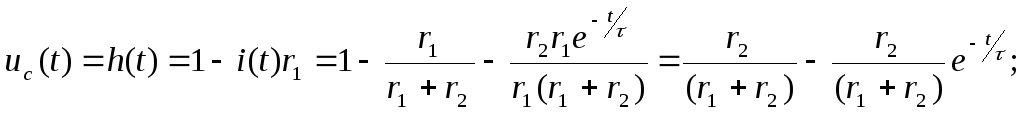
Здесь мы учли, что U₀=1 B, а выходное напряжение равно напряжению конденсатора.

6. 39^*

На входе цепи r, L напряжение имеет форму, изображённую на рис. 6. 38. Рассчитать ток в цепи.

Решение: Для цепи r, L переходная проводимость записывается в виде: . Расчёт тока ведём по интервалам. На первом из них:, u(0)=U₀; u(t)=U₀; u′(t)=0.

Поэтому из общей формулы интеграла Дюамеля: остаётся только первый член, включающий начальный скачок напряжения: .

На втором интервале: T ≤ t ≤ ∞, u(T)= -2U₀; u(t)= -U₀e^-αt; u′(t)=αU₀e^-αt; u′(x)=αU₀e^-αt

Интеграл Дюамеля, с учётом тока на предыдущем интервале запишется в виде:

6.45.* Для четырехполюсника (рис. 6.44) получить выражение передаточной функции по напряжению, а также записать выражение амплитудной, фазовой, вещественной и мнимой частотных характеристик, используя передаточную функцию по напряжению.

В цепи: r=10 Ом; L=0,05 Гн; C=100 мкФ.

Решение: Передаточной функцией по напряжению Ku(p) является отношение выходного напряжения к входному:

.

В операторной форме входное сопротивление цепи равно:

.

Входной ток: ;

Входное напряжение: .

Передаточная функция по напряжению: ;

Заменим p на jω

;

Умножаем числитель и знаменатель на число, комплексно-сопряженное знаменателю:

;

.

Выделив вещественную и мнимую части полученного выражения, получаем вещественную и мнимую частотные характеристики:

;

.

Передаточную функцию Ku(jω) можно также представить в виде:

,

где А(ω) - амплитудно-частотная характеристика, а (ω) – фазовая частотная характеристика.

В нашем случае:

;

.

Для изображения частотных характеристик часто используют логарифмический масштаб, то есть, частота по оси абсцисс откладывается таким образом: 1, 10, 10², 10³ и т.д.

Логарифмической амплитудно-частотной характеристикой является:

.

В нашем случае:

.

Амплитудная, фазовая, а также логарифмическая амплитудная характеристики приведены на рис. 6.45.

Следует также отметить, что если требуется рассчитать только А(ω) и (ω), то удобнее использовать комплексное выражение Ku(jω), так как в этом случае расчет амплитуды и фазы сигнала ведется по одной формуле.

рис. 6.45.