Новая папка / Примеры для решения6

6. Переходные процессы в линейных электрических цепях.

6.1. Классический метод анализа.

6.2. В цепи (рис. 6.3.)

Uо=120В; E=80 В r=1 кОм ;

C=10 мкФ. Рассчитать напряжение и ток на конденсаторе после коммутации (ключ перебрасывается из нижнего положения в верхнее), а также определить в какой момент времени напряжение конденсатора будет равно нулю?

6.3. Определить ток в цепи

рис. 6.4. и напряжение на индуктивности после коммутации , если E₁=20 B E₂=60 B; r=40 Ом; L=0,04 Гн.

6.4.

Качественно построить кри-вые U_C1(t) и U_C2(t) после замыкания ключа (Рис. 6.5.) для двух случаев :

а) R>>r (C₁=C₂=C)

б) r>>R

6.5.

Определить величину R, в цепи (рис.6.6.) при котором время переходного процесса будет минимальным, если E=100 B; r=25Ом; L=0,5 Гн, а катушка индуктивности рассчитана на напряжение до 500 В?

Рассчитать переходный процесс в цепи (рис. 6.8), возникающий после коммутации. Определить и , если ;Ом; С=250 мкФ.

6.8

Определить ток в цепи (рис. 6.9) после коммутации, если ; r=10 Ом; L=0.1 Гн.

6.9

Найти и в цепи (рис. 6.10) после коммутации, если:; Ом; .

6.11.

Определить напряжение на ёмкости (рис. 6.12) и ток через ёмкость после замыкания ключа, если U₀=100В; r₁=40 Ом; r₂=60 Ом; С=50 мкФ.

12. Решить задачу 6.8 путём сведения ненулевых начальных условий к нулевым.

6.14.

Определить, как будет меняться напряжение на конденсаторе после размыкания ключа (рис. 6.14).

Напряжение на входе цепи:

Параметры цепи:

r₁=200 Ом; r₂=100 Ом; С=120 мкФ.

6.15. Цепь r, L (r=10 Ом; L=0,2 Гн) включается на синусоидальное напряжение

При какой начальной фазе напряжения -  в цепи будет наблюдаться максимальный бросок тока? В каком случае переходного процесса в цепи не будет?

6.16. Определить максимально возможное напряжение на конденсаторе в цепи r, C, которая включается на синусоидальное напряжение , если r=60 Ом; С=18 мкФ.

При какой начальной фазе напряжения источника переходного процесса не будет?

6.18.

Определить значения всех токов и напряжений при t=0₊ для цепи (рис.6.16), если U₀=120 B; r₁=100 Ом; r₂=20 Ом.

6.19.

Найти значения токов i₂(0) и i₃(0) в цепи (рис. 6.17) при U₀=160B; r₁=40 Ом; r₃=80 Ом.

6.20.

Найти начальные значения напряжения на катушках индуктивности после замыкания ключа, если U₀=200B; r₁=200 Ом; r₂=100 Ом.

6.22.

Определить характер переходного процесса в цепи (рис.6.20), если r₁=100 Ом; r₂=2 Ом; L=0,1 Гн; С=200 мкФ.

6.23.

Рассчитать u_c(t) после замыкания ключа, если U₀=200 B; r=200 Ом; L=1 Гн; С=100 мкФ.

6.24.

Рассчитать ток в цепи после размыкания ключа.

U₀=10 B; L=0,5 Гн; С=20 мкФ;

r₁=20 Ом; r₂=30 Ом.

6.25.

U₀=40 B; r=20 Ом; L=0,1 Гн;

С=100 мкФ.

Рассчитать u_c(t) и i(t) после размыкания ключа.(рис. 6.23).

6.2. Операторный метод анализа

6.27.

U₀=50 B; r=100 Ом; С=100 мкФ;

Рассчитать ток в цепи (рис. 6.20) и напряжение на конденсаторе после размыкания ключа, используя операторный метод.

6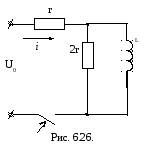.28.

U₀= 120 B; r = 40 Ом; L= 0,6 Гн;

Найти ток в цепи (рис. 6.26) операторным методом.

6.29.

а) б)

Рассчитать выходное напряжение четырёхполюсника, если на входе напряжение спадает в соответствии с графиком (рис. 6.27-б) и качественно построить график U₂(t).

6.30.

Получить формулу для U₂(t) в общем виде, если на входе цепи (рис. 6.28) действует напряжение U₁(t)=U₀e^-t. Качественно построить график U₂(t).

6.32.

Рассчитать ток, потребляемый цепью(рис. 6.31) от источника, после размыкания ключа операторным методом, если:

U₀=20 B; r₁=20 Ом; r₂=20 Ом; L=0,05 Гн; С=100 мкФ.

6.33.

Найти U_L(t) (рис. 6.32) после размыкания ключа операторным методом, если U₀=150 B; r=75 Ом; L=0,01 Гн; С=20 мкФ.

6.34.

Напряжение на входе цепи (рис. 6.33) u=120sin(314t+90⁰);

Параметры цепи: r=20 Ом; L=0,1 Гн.

Рассчитать ток в цепи после размыкания ключа операторным методом.

6.35.

Рассчитать ток и напряжение на конденсаторе операторным методом, если u=200sin(314t+45⁰),B; r=100 Ом; С=120 мкФ.

6.36.

Рассчитать напряжение на конденсаторах в цепи (рис. 6.35), если: U₀=100 B; r=100 Ом; С₁=С₂=100 мкФ. (Рекомендуется привести цепь к нулевым условиям).

Примечание: Начальное значение напряжения на конденсаторе, последовательно к которому подключён рубильник равно нулю.

6.3. Анализ переходных процессов методом наложения (Интеграл Дюамеля).

6.38

Получить выражение переходящих функций по напряжению для схем, изображённых на рис. 6. 37.

6.40.

Рассчитать напряжение на входе четырёхполюсника, (рис. 6.39), если U₀=20B; r=100 Ом; С=100 мкФ; Т=2^.10^-2 с.

6.41.

Определить выходное напряжение четырёхполюсника (рис 6.40), если U₀=20B; L=0,1 Гн; r=20 Ом; Т=0,01 с.

6.42.

Цепь задачи 6.40 включается на последовательность прямоугольных импульсов (рис. 6.41). Получить в общем виде выражение для u₂(t)

6.43.

Четырёхполюсник задачи 6.41 подключается к источнику прямоугольного напряжения (рис.6.42). Получить в общем виде выражение для выходного напряжения четырёхполюсника -u₂(t).

6.44.

L = 0,1 Гн; C = 200 мкФ;

r = 50 Ом; U_m =100 В; T = 0,02с.

Найти выходное напряжение u₂(t) и построить его график для цепи (рис. 6. 43).

6.4. Передаточные функции. Частотные характеристики.

6.46. Определить передаточные функции по напряжению, а также рассчитать амплитудно-частотные (АФХ) и фазо-частотные характеристики и построить их графики для интегрирующего и дифференцирующего звена (рис. 6.46), если r=100 Ом; C=0,5 мкФ.

а) рис.6.46. б)

6.47. Рассчитать и построить на графике АЧХ и АФХ низкочастотного фильтра (рис. 6.47), если C=100 мкФ; r=10 Ом.

рис. 6.47.

6.48. Рассчитать и построить графики ЛАЧХ и ЛФЧХ для четырехполюсника (рис. 6.48). Параметры цепи: r=100 Ом; L=0,002 Гн; C=2 мкФ.

рис. 6.48.

6.49. Получить выражение передаточной функции для цепи (рис. 6.49), а также формулы ВЧХ и МЧХ. Привести графики АЧХ, ФЧХ, ВЧХ и МЧХ, если r=100 Ом; L=0,01 Гн; C=5 мкФ.

рис. 6.49.

5. r Найти U_L(0); U_L(t), а также

качественно построить U_L(t)

U_O L

r

5. Конденсатор емкостью С = 100 мкФ заряжен до напряжения

U_C (0) = 200 В. Какая энергия выделится при разряде этого конденсато-

ра через резистор R = 1 кОм ?

5.1. 2 Вт 5.2. 4 Вт 5.3. 40 Вт 5.4. 200 Вт

5. Записать выражения U_C(t) после размыкания ключа.

r

U_O C r

5. Изобразить U_C1(t) и U_C2(t), если С₁ = С₂ , R₁R₂,

U_C2(0) = 0.

R1 R2

U_O C1 C2

5. При полной разрядке конденсатора емкостью С = 200 мкФ

на сопротивлении резистора выделяется в виде тепловой энергии 1 Дж.

Спустя 0,06 с после начала разрядки напряжение на обкладках конденсатора равнялось 5 В. До какого напряжения был заряжен конденсатор и каково сопротивление, через которое он разряжается ?

5. 5. При полной разрядке конденсатора емкостью С = 200мк

на сопротивлении резистора выделяется в виде тепловой энергии 1 Дж.

Спустя 0,06 с после начала разрядки напряжение на обкладках конденсатора равнялось 5 В. Через какой промежуток времени после начала разрядки напряжение конденсатора упадет до 0,001 % своего первоначального значения ?

5. Конденсатор С₁ = 10 мкФ, предварительно заряженный до напряжения U₁ = 100 В, замыкается на цепь, состоящую из последовательно соединенных резистивного сопротивления R = 125 Ом

и заряженного до напряжения U₂ = 20 В конденсатора С₂ = 40 мкФ.

Найти как функцию времени ток в цепи и напряжение на обкладках каждого конденсатора, а также построить графики найденных функций. Найти величину энергии электрического поля до замыкания контакта и по окончании переходного процесса.

R

+ +

- C1 C2 -

5. Конденсатор емкостью С = 50 мкФ, заряженный предварительно до напряжения U = 500 В, разряжается через цепь, резистивное сопртивление которой R = 100 Ом и индуктивность

L = 10 мГн. Определить, через какой промежуток времени, считая от начального момента разряда, ток в цепи достигнет максимального значения и какова величина последнего.

5. Конденсатор емкостью С = 50 мкФ, заряженный предварительно до напряжения U = 500 В, разряжается через цепь, резистивное сопртивление которой R = 100 Ом и индуктивность

L = 10 мГн. Вычислить в какой момент времени в индуктивной катушке наведется максимальная ЭДС, найти ее значение.

5. Записать интеграль Дюамеля для выходного напряжения U₂(t)

при включении цепи на напряжение U₁(t), если известна ее переходная

функция по напряжению h(t).

U₁(t)

U₁

U₂

0 t₁ t₂ t

5. До замыкания котакта К в цепи имел место установившийся режим постоянного тока. Определить токи и напряжения на индуктивности для момента замыкания контакта t= 0₊ и для установившегося режима (t =). Дано: R1=R2=R4=100 Ом,

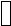
R3=R5= 200 Ом, L= 10 мГн, С = 1 мкФ и Е = 120 В.

R1 R4

R2

Е К С

L

R5

R3

5. Цепь включается на постоянное напряжение U= 125 В. Найти

выражение напряжения на конденсаторе при R = 250 Ом, L = 667 мГн,

С = 2 мкФ .

R

L C

U i₁

i₂ i₃

5. Цепь включается на постоянное напряжение U= 125 В.

Найти выражение напряжения на конденсаторе при R = 100 Ом,

L = 40 мГн, С = 1 мкФ.

R

L C

U i₁

i₂ i₃

5. Цепь включается на постоянное напряжение U= 125 В.

Найти выражение напряжения на конденсаторе при R = 100 Ом,

L = 40 мГн, С = 5 мкФ.

R

L C

U i₁

i₂ i₃

5. Цепь, состоящая из последовательно соединенных R и С, включается на прямоугольный импульс напряжения U, действующий в течении времени t_И . Найти выражение напряжения на емкости U_C(t) в зависимости от времени.

U

0 t_Н t

5. Цепь, состоящая из последовательно соединенных R и С, включается на прямоугольный импульс напряжения U, действующий в течении времени t_И . Найти ток i(t) в зависимости от времени.

U

0 t_Н t

5. Найти выходное напряжение U₂ , если на вход подается линейно растущее напряжение U₁ =U_Ot.

1 2

L

U₁(t) C U₂(t)

1¹ 2¹

5. Определить закон изменения ЭДС е₂(t) возникающей во вторичной обмотке трансформатора при замыкании ключа К.

К

Е

L₁ L₂ е₂

5. После того как ток в электрической цепи можно было считать

установившимся, замкнулся ключ К .

Е

R

L

R

К

5. В цепи замыкается ключ К. Найти установившиеся значения токов в каждой из катушек, если L₁ = L, а L₂ = 4L, считая сопротивления самих катушек равным нулю.

L₁