Новая папка / Примеры для решения2

2. Линейные электрические цепи синусоидального тока.

2.1. Анализ простых цепей синусоидального тока.

2.2. В последовательной цепи r,L действующее значение тока I=2A при r=10Ом; ωL=12Ом.

Записать мгновенное значение напряжения на зажимах цепи, считая, что частота тока и напряжения f=50Гц.

2.3. Приложенное напряжение равно U=10 В, частота источника

=5000 С^-1, R=16 Ом, С=25 мкФ. Цепь находится в резонансе. Определить L. Полагая, что u=Usint, построить зависимости от времени мгновенных токов i, i_L, i_C и мгновенных мощностей p_L, p_C, p

2.4. Дано: u_C1 = 42sint

R1= 48 Ом

R2=22 Ом

X1=21 Ом

X2=25 Ом

Используя комплексные числа, найти i1, i2, и i3 , а также приложенное напряжение в схеме рис.2.1

2.5. Дано: u_C1 = 42sint

R1= 48 Ом

R2=22 Ом

X1=21 Ом

X2=25 Ом

Используя комплексные числа, найти i1, i2, и i3 , а также приложенное напряжение в схеме рис.2.2.

2.6. По нагрузке рис.2.4 протекает ток i = 10sin (t -25⁰)

и к ней приложено напряжение

u = 120sin (t +15⁰)

Определить составляющие этой нагрузки (R и X)

Рис.2.4

2.7. Дано: U= (90+ j70) B

I = (26 -j17) A. Определить R и X , угол между напряжением и током, S, P, Q нагрузки рис.2.4

2.8. В последовательной цепи r,L,C при частоте f=50Гц r=100Ом; X_L=200Ом; X_C=100Ом.

При какой частоте в цепи возможен резонанс?

2.9. Известно, что в последовательной колебательном контуре при резонансной частоте 2.5 кГц отношение напряжения на конденсаторе к напряжению на входе равно 50. Емкость С=0.6 мкФ. Вычислить R и L контура.

2.10. Найти полное сопротивление двухполюсника синусоидальному току частотой 60 Гц и постоянному току, если R=25 Ом, С=170 мкФ

2.11. Дано: R1=40 Ом, X_L=30 Ом., X_C=15 Ом. Чему равно R2 при резонансе токов и каково при этом полное сопротивление цепи рис.2.5.

2.12. В цепи с активным сопротивлением и емкостью r=10Ом; X_C=10Ом. При последовательном соединении элементов активная мощность P=10Вт.

Определить активную, реактивную и полную мощность при параллельном соединении активного сопротивления и емкости, считая напряжение источника питания неизменным.

2.13. В цепи резонанс. Построить векторную диаграмму токов и топографическую напряжений и определить X_L, X_C, R, если заданы I1=3 A, I2=5 A, P=250 Bт

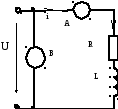
2.14 Найти параметры катушки (R,L), емкость С конденсатора и сопротивление R1, включенного в цепь в соответствии с рис.2.7, если при резонансе приборы показали U=200 B, U1=204 B, U2=180 B, I = 4 A. Частота переменного тока 50 Гц.

2.15. Катушку индуктивности подключили в цепь постоянного тока, а затем в цепь переменного тока частотой 2.8 кГц. При этом измерительные приборы соответственно показали

U₀ = 30 В I₀ = 2.5 A

U =120 B I = 6 A

Определить R и L катушки

2.16. Катушку индуктивности подключили в цепь постоянного тока, а затем в цепь переменного тока частотой1.8 кГц. При этом измерительные приборы соответственно показали

U₀ = 60 В I₀ = 5 A

U =120 B I = 6 A

Определить R и L катушки

U1

2.17. Найти параметры катушки (R,L), емкость С конденсатора и сопротивление R1, включенного в цепь в соответствии с рис., если при резонансе приборы показали U=250 B, U1=254 B, U2=190 B, I = 5 A. Частота переменного тока 60 Гц.

2.18. В цепи резонанс. Построить векторную диаграмму токов и топографическую напряжений и определить X_L, X_C, R, если заданы I1=6 A, I2=10 A, P=500 Bт

2.20. В цепи (рис. 2.2) ωL=50Ом; r=200Ом; 1/ωC=200Ом; I₃=1A.. Определить напряжение на зажимах.

2.21. Дано: U=60B; r₁=20Ом; r₂=40Ом; X_L1=X_C1=40Ом; X_L2=X_C2=50Ом;

Определить показания приборов в схеме рис. 2.3

2.2. Анализ цепей синусоидального тока с помощью векторных диаграмм.

2.23. По показаниям трех амперметров I₁=6.5А , I₂=3.5А, I₃=4А определить активную мощность , расходуемую в ветви с R₁L. Примечание: Задачу начать решать с помощью диаграммы токов, если R₂=30 Ом

2.24. По показаниям трех амперметров I₁=6.5А , I₂=3.5А, I₃=4А определить активную мощность , расходуемую в ветви с R₁L. Примечание: Задачу начать решать с помощью диаграммы токов, если мощность, расходуемая в сопротивлении R2 равна 480 Вт

2.25. В цепи резонанс. Построить векторную диаграмму токов и топографическую напряжений и определить R, X_L, X_C, если U_вх=50 В, Р=50 Вт, U₁₂=70.7 В, U_C=50B

2.26. Определить напряжение на зажимах цепи с помощью векторной диаграммы, если:

I₃=1A; r₁=10Ом; r₂=r₃=20Ом; X_L=X_C=20Ом.

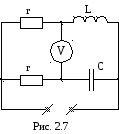
2.27. С помощью векторной диаграммы токов и напряжений определить показания вольтметра в схеме рис. 2.7, если U=20B; r=10Ом; X_L=10Ом; X_C=10Ом.

2.28. Найти показания амперметра в цепи рис. 2.8, если при r=10Ом; X_L=10Ом; X_C=10Ом вольтметр показывает напряжение 10В.

2.29. В цепи изображенной на рис. 2.9 ток активно-индуктивной нагрузки I_H=10A при коэффициенте мощности этой нагрузки cosφ_н=0,707. Напряжение на зажимах U=100B.

Рис. 2.9

Определить емкостное сопротивление конденсатора, подключенного в параллель к нагрузке, при котором ток в неразветвленной части цепи примет минимально возможное значение. Чему равен этот ток?

2.3. Анализ цепей синусоидального тока символическим методом.

2.30^* Рассчитать все токи в цепи, определить активную и реактивную мощность, потребляемую цепью, определить мощность источника, если r₁=10Ом; X_C1=10Ом; X_L=20Ом; r₂=20Ом; X_C2=30Ом; U=40B.

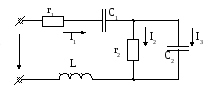
Рис. 2.10

Решение

Находим комплексное сопротивление цепи

Ток в неразветвленной части цепи:

Напряжение на элементах r₂, C₂

Токи в r₂ и C₂

Активная мощность приемника

Реактивная мощность приемника

Мощность источника

Отсюда: P_H=67Вт; Q_H=2,16ВАр.

Таким образом, расчет токов в цепи выполнен верно, что подтверждает баланс активной и реактивной мощности.

2.31.

а) б)

Дано: U=20B; r=10Ом; X_L=10Ом; X_C=10Ом.

Определить показания амперметров в схемах рис. 2.11,а и 2.11,б

2.32. Рассчитать сопротивления цепи рис. 2.12, если r₁=10Ом; r₂=20Ом; X_C1=40Ом; X_L1=10Ом; X_C2=20Ом; X_L2=10Ом.

2.33. Рассчитать зависимость модуля и фазы сопротивления цепи рис. 2.13 от частоты – Z(ω)=?; φ(ω)=?, если L=0,01Гн; C=100мкФ; r₁=20Ом.

2.35. Дано: Ė₁=4В; Ė₂=4e^-j90°; r=2Ом; X_C=2Ом; X_L=4Ом.

Рассчитать все токи в цепи рис. 2.15 методом двух узлов.

2.36.Дано: Ė₁= Ė₂=6В; X_L=2Ом; r=2Ом.

При разомкнутом ключе найти ток в сопротивлении r методом эквивалентного генератора.

При каком значении емкостного сопротивления (ключ разомкнут) ток İ будет совпадать с напряжением по фазе?

2.37. Дано: Ė=5В; r=2Ом; X_L1=2Ом;

X_C=4 Ом; X_L2=4 Ом.

Рассчитать все токи в цепи рис. 2.17, используя метод переноса источника ЭДС за узел.

Построить векторную диаграмму токов и топографическую диаграмму напряжений на комплексной плоскости.

2.38. Дано:

E=10B; r₁=r₂=5Ом; X_L=X_C=5Ом.

Определить показания вольтметра и ваттметра в цепи рис. 2.18.

2.39. Генератор питает линию передачи электрической энергии и отдает мощность P1=29 кВт. Напряжение генератора U1=3кВ. Параметры линии Rл=30 Ом Xл=55 Ом. Мощность , потребляемая нагрузкой в конце линии P2=27 кВт. Определить параметры нагрузки?

*

2.40. Измерительные приборы показали при подключении к цепи переменного тока частотой 50 Гц:

Р= 130 Вт U=83 В I= 6 А

Определить активное сопротивление и индуктивность

2.41. Цепь состоит из индуктивной катушки (RL) , соединенной последовательно с конденсатором без потерь. Приложенное ко всей цепи напряжение U = 40 В. Определить напряжение на катушке при резонансе , если при этом напряжение на конденсаторе равно 150 В.

2.43. Дано:

E₁=4B; r₁=2Ом; X_L=2Ом; X_C=2Ом; r₂=1Ом; Ė₂=4e^j90°В;

Определить показания вольтметров (рис. 2.20).

2.44. Дано:

Ė₁=4e^j45°B; Ė₁=4e^-j45°B; r=20Ом; X_C=2Ом; X_L=4Ом.

Определить показания ваттметра рис. 2.21 (Рекомендуется использовать метод двух узлов).

2.45. Дано:

Ė=10В; r=30Ом; X_L=10Ом; X_C=10Ом.

Определить напряжения между точками a и b и b и c в цепи рис. 2.22.

2.4. Электрические цепи с взаимной индукцией.

2.47. В цепи из двух одинаковых последовательно включённых индуктивно-связанных катушек приборы показали следующее: U=60B; P=20Вт; I=1A. После того, как зажимы поменяли местами, амперметр зарегистрировал ток I=2,4A. Определить коэффициент индуктивной связи между катушками.

2.48. Две одинаковые индуктивно-связанные катушки соединены последовательно. При напряжении на зажимах цепи: U=100 B ток при согласном включении катушек со-ставил 2А. Чему будет равен ток при встречном включении катушек, если коэффици-ент индуктивной связи равен 0,6? (Активным сопротивлением можно пренебречь.

2.49. Две одинаковые катушки соединены последовательно. Определить коэффициент связи между ними, если ток при согласном включении катушек в 8раз меньше, чем ток при встречном включении? (Активным сопротивлением катушек можно пренебречь.)

2.50. На первичной обмотке идеального трансформатора U₁=100 В, число витков первичной и вторичной обмоток соответственно равно: ω₁=500; ω₂=100. Сопротивление нагрузки вторичной обмотки: R_H=100 Ом. Определить ток первичной обмотки трансформатора.

2.51. Ток в первичной обмотке воздушного трансформатора (рис.2.24.) I₁=02А. Определить показания вольтметра, если r₁=2 Ом;r₂ =4 Ом; ωL₁=100 Ом; ωL₂=200 Ом.

2.52. Определить ток первичной обмотки воздушного трансформатора предыдущей задачи, если вместо вольтметра (рис.2.24.) включено активное сопротивление R=200 Ом, а напряжение на первичной обмотке U₁=200 В.

2.53. Определить показания вольтметра в цепи рис. 2.25.

U=50 B; r=50 Ом; ωL₁=100 Ом; ωL₂=100 Ом;

2.5. Геометрические места точек на комплексной плоскости. (Годографы сопротивлений, проводимостей и токов.)

2.54.* Изобразить годографы сопротивлений и проводимостей для цепей, изображен- ных на рис.2.26.(Сопротивление элемента со стрелкой изменяется от нуля до бесконечности). Определить Г.М.Т.=?

Г.М.Т.=?

Построение Г.М.Т. и Г.М.Т. показано на рис2.27.

a) Г.М.Т. Г.М.Т.

б) Г.М.Т. Г.М.Т.

в) Г.М.Т. Г.М.Т.

Рис. 2.27.

2.55.* Построить для цепи (рис. 2.28.) годограф сопротивления, если r₁=10 Ом; r₂=20 Ом; X_L=0.

L

a

Рис.2.28.

Данную задачу решают в два приёма. Сначала строят годограф сопротивления параллельного участка, а затем к нему суммируют постоянный вектор r₁.

а) Г.М.Т. б)

2.56. Построить годограф сопротивления для цепи, изображённой на рис.2.30., если ₁=20е ^j45 Ом; X_c=20 Ом; r=0.

Рис.2.30.

2.57. Построить годограф сопротивления для цепи (рис.2.31.), если ωL=60 Ом; r=100 Ом; 1/ωc=0.

Рис.2.31.

2 .59. Построить круговую диаграмму тока при изменении активного сопротивления от нуля до бесконечности, если U=60 B;

ωL=60 Ом. (рис.2.34.)

60. Построить круговую диаграмму тока в цепи рисунка 2.35, если U=40 B; r=40 Ом; X_C=0.

2.62. Рассчитать и построить круговую диаграмму тока в активном сопротивлении r₂,

если Е=60 В; r₁=30 Ом; Х_L=40 Ом; Х_С=40 Ом. (схема изображена на рис.2.38.)

2.63.Рассчитать и построить круговую диаграмму тока рис.2.39., если Е=10 В; r₁=2 Ом;

ωL=5 Ом; 1/ωС=50 Ом; r₂=0.

64. В; В; r₁=0; r₂=4 Ом; ωL=4 Ом; 1/ωC=4 Ом. Рассчитать и построить круговую диаграмму тока для цепи рис.2.40.