Примеры решения задач по второй части теоретического материала

2.1.* В цепи r,L,C (все элементы соединены последовательно) r=50 Ом; L=0,318 Гн; C=63,6 мкФ. Напряжение на зажимах B. Частота синусоидального напряжения f=50Гц.

Найти ток (мгновенное и действующее значения), активную, реактивную и полную мощности, а также падения напряжения на всех элементах.

Решение:

Определяем реактивное сопротивление при f=50Гц:

Индуктивное:

Емкостное:

П олное сопротивление:

Амплитуда тока в цепи:

Действующее значение тока:

Сдвиг по фазе между током и напряжением:

Ввиду того, что индуктивное сопротивление является преобладающим, ток отстает по фазе от напряжения на .

Мгновенное значение тока:

Активная мощность:

Реактивная мощность:

Полная мощность:

Падение напряжения на отдельных элементах:

2.19. * В цепи (рис. 2.1) U=100B; r₁=50Ом; r₂=100Ом; X_C=100Ом.

Найти все токи и определить активную и реактивную мощности.

Решение:

Участок с параллельным соединением r₂ и C преобразуем в последовательную эквивалентную цепочку.

Проводимость этого участка

Сопротивление участка:

Фазовый сдвиг:

Эквивалентное активное и емкостное сопротивления:

Полное сопротивление цепи:

Ток в неразветвленной части цепи:

Напряжение на параллельном участке:

Токи I₂ и I₃ будут равны:

Активная мощность в цепи:

Реактивная мощность:

2.22.* Найти все токи в схеме цепи (рис. 2.4), используя векторную диаграмму токов и напряжений, если U=40B; r₁=20Ом; X_L1=40Ом; X_C=40Ом.

Решение:

Задаемся током в одной из параллельных ветвей, например, примем I^'₂=1A (знак "штрих" означает, что это не реальное значение тока).

Откладываем вектор I₂ в масштабе токов на диаграмме (рис. 2.5).

Так как в сопротивлении ток и напряжение совпадают по фазе, то вектор U₂ откладываем вдоль I₂ в масштабе напряжений.

Ток через конденсатор:

Вектор тока I₃ откладываем под углом к напряжению U₂, так как ток в емкости опережает напряжение по фазе на этот угол.

Ток I^'₁ находится как векторная сумма токов I^'₂ и I^'₃.

В нашем случае, когда угол между ними равен модуль тока I^'₁ можно найти по формуле:

Напряжение на индуктивности:

Этот вектор откладывается из конца U₂ под углом к току I₁, ввиду того, что напряжение на индуктивности опережает ток на .

Падение напряжения на сопротивлении r₁:

Так как ток и напряжение на активном сопротивлении совпадают по фазе, то этот вектор откладывается из конца U_L параллельно току I₁.

Если теперь соединить начало координат с концом вектора U_r1, то получим напряжение на зажимах цепи.

В нашем случае модуль этого вектора оказался равным

Сравниваем полученный результат с заданным напряжением U и определяем коэффициенты пересчета:

Теперь определяем действительные значения токов в ветвях:

2.34.*

Дано: r₁=2Ом; r₂=1Ом; X_C=3Ом; X_L=2Ом. Определить все токи методом контурных токов, рассчитать баланс мощности, построить векторную топографическую диаграмму напряжений.

Решение:

Система уравнений в общем виде примет вид:

Подсчитываем коэффициенты системы уравнений

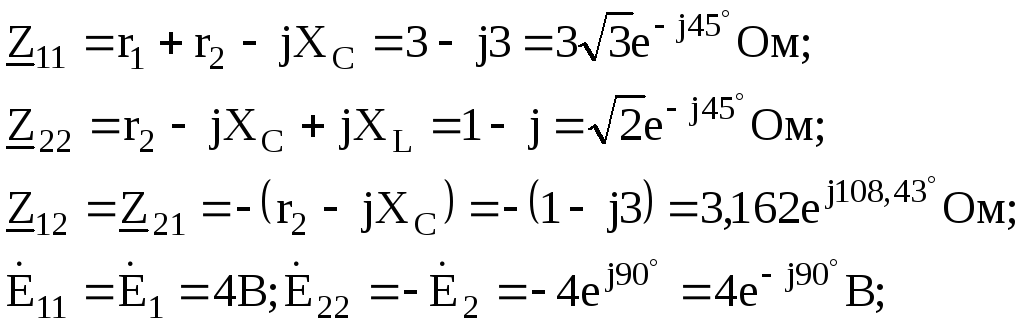
Система уравнений с численными значениями коэффициентов:

Решаем эту систему методом определителей

Токи в ветвях:

Подсчитываем баланс мощности.

Мощность источников:

Мощность приемников:

Далее рассчитываем векторную топографическую диаграмму.

Примем

Тогда

Диаграмма приведена на рис. 2.15.

Рис. 2.15

2.42^*. Дано: r₁=35Ом; r₂=50Ом; r₃=50Ом; r₄=42Ом; X_L1=4Ом; X_C1=24Ом; X_C2=27Ом; Ė₁=39,7B; Ė₂=42,6e^-j60°B; Ė₃=45,4e^j90°B.

Определить показания вольтметров.

Рис. 2.19

Решение:

Для решения задачи необходимо определить потенциалы узлов, между которыми включены вольтметры. Очевидно, удобнее всего это сделать, воспользовавшись методом узловых потенциалов.

Примем

Узловые проводимости и проводимость между узлами 1 и 2 будут равны:

Узловые токи:

Система уравнений в матричной форме записи имеет вид:

Расчет этой системы по определителям дает следующие результаты:

Показания вольтметров:

2.46* Две катушки индуктивности вклю-чены последовательно. При этом катушки связаны через общее магнитное поле. Параметры катушек:r₁=10 Ом; ωL₁=20 Ом; r₂=20 Ом; ωL₂=20 Ом.

Определить, как включены катушки (согласно или встречно), если при напряжении на зажимах цепи U=60В, ток в цепи равен 2А? Найти коэффициент индуктивной связи между катушками и падение напряжения на каждой из катушек ( К=? U1=? U2=? ).

Решение: Полное сопротивление цепи определяется по закону Ома:

Д ля последовательного включения индуктивно-связанных катушек сопротивление цепи при согласном и встречном включении равно:

Подстановка численных данных в первую из этих формул показывает, что катушки не могут включены согласно, так как даже при М=0 сопротивление оказывается >30 Ом. Делаем вывод , катушки включены встречно.

Отсюда;

;

Значит, ; Ом;

К оэффициент индуктивной связи между катушками:

П адения напряжениий на катушках равны:

2.58*. U=100 B; r=50 Ом; ωL=50 Ом; 1/ωс=0.

Построить круговую диаграмму тока в цепи при изменении емкостного сопротивления от нуля до бесконечности.

Решение:

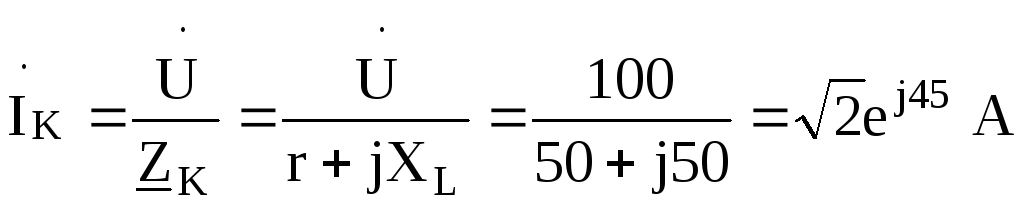Находим ток короткого замыкания в цепи, считая, что X_C=0:

Д алее на комплексной плоскости (рис.2.33.) откладываем векторы и .Затем находим ток в цепи для произвольного значения X_C, например, при X_C=100 Ом.

и откладываем этот вектор на комплексной плоскости. Для определения центра окружности токов делим векторы и пополам и из середины каждого вектора проводим перпендикуляры в точке пересечения которых и будет находиться центр окружности токов.Сопротивление короткого замыкания Z_K откладывается параллельно вектору тока I_К. Из конца Z_K проводится линия переменного сопротивления. В нашем случае эта линия будет перпендикулярна вектору напряжения на зажимах цепи -, так как переменным сопротивлением является ёмкость.

2.61.* Построить круговую диаграмму тока через конденсатор при изменении ёмкост-ного сопротивления от нуля до бесконечности рис.2.36.-а, если =6 В; = ^-j90 B; r₁=2

Ом; r₂=2 Ом; X_C=2 Ом.

а) б)

а

б

в)

Решение:

Задача решается c использованием метода эквивалентного генератора. При этом схема цепи сводится к двум последовательно включенным сопротивлениям, одно из которых является переменным (рис.2.36.-а, б, в.). Определяем напряжение холостого хода на зажимах а и б (рис.2.36.-б)

А. .

Сопротивление короткого замыкания цепи:

Ток короткого замыкания:

Далее находим ток при произвольном значении ёмкостного сопротивления. Примем X_C=2 Ом.

А.

Построение круговой диаграммы выполняется также, как и в задаче 2.38. и становится ясным из рис.2.37.

Рис.2.37.