Этот элемент инвертор

2) Если a) r_ос>r₁ k>1

r оc.

r - Умножитель

3) Если

т. е. Этот решающий блок будет выполнять функцию интегрирования

с

r1

u

r₁c = кратно 10

rос

r1 -(U₁+U₂+U₃)

U₁ - Сумматор

r₁

U₂

r₁ r₁=r_ос

U₃

Составим Б – С для математического моделирования

U

Блок нелинейности

- i

-ri

к осцилографу

^

i

-ir r – коэффициент передачи

Замкнутый контур должен содержать нечетное число решающих элементов

w_c

i

Вт

_I1 w_c

r₁L U

U

Дано

u = u_msinwt

w_c w_B _c L_c r_B L_B

(i), r, L

Найти

i_n U_n i₁

Это вольтодобавочный регулятор

С

оставим систему нелинейных ДУ по законам К

1) -

2

) -

=

3)

Получим систему из трех уравнений (1, 2, 3)

4)

Решим систему ДУ способом моделирования решающими блоками. Возведем в квадрат составляющие в которых есть произведение.

Уравнение (3) подиферентцируем

Т. к. из уравнения (4)

Таким образом уравнение (3) примет вид

Из этого уравнения найдем

Перепишем уравнение выделяя отмеченные сост. В левых частях

Система решающих блоков готова.



u

-r_bi_b -L_bi_b

d_b dt



НБ_1­

НБ₂



Блоки для вычисления k()

Рассчет нелинейных цепей с ключевыми (вентильными) элементами

e1=E₁msinwt E₀=0.5E₁m H₁ E_O r₁=r₂

H₁ и H₂ идеальные

i₁

e₁ r₁ Найти i₃

i₃

Такие цепи обычно считаются ме‑

e₁ i₂ тодом кусочно – линейной аппрокси‑

H₂ мации

1 кв - r = 0

r2 2 кв - r = 

1

i

2 U

Условия для

Проверяют по току.

U0 – закрывается

i0 – открывается

Т. к. процессы в цепи периодические то достаточно рассмотреть рассчеты на одном периоде

e₁

E₀

E_m  2 t

t₁ t₂

i’₃

t

i’’₃

I’’’₃

Построим временные диаграммы

Определим возможные пути токов на с сопротивлением r₁

Находим временные интервалы выделенных путей токов

1. Пусть i’₃ будет протекать если

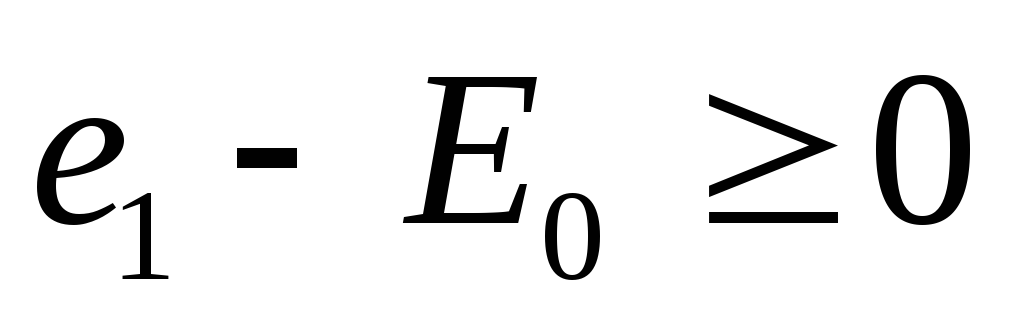
это точки выделены. На диаграмме интервал (t₁ t₂)

Записываем закон К-а для этого контура

(справедливо от t₁ до t₂)

t₁ и t₂ находим из условия e₁-E₀=0

Одновременно по второму контуру протекает ток

2) Тоже ток в интервале (0;)

строим его

3) В интервале ( - 2)

Знаменатель в два раза меньше 

i₃­

 2

i₃

U’d₁ 1 2 e₁ = E₁msinwt

E₀ E₀ =

Диоды идеальные

+ r₁ = r₂

H_1­ H₂

e₁ ir₂

(+) r₁ r₂

ir₁`

3. 4

Найти напряжение на нелинейных элементах

Определим возможные пути протекания токов в схеме

Em

 2 t

t₁ t₂

1 - 4 2 - 3

t

1 2

определены

Только источник e₁способствует протеканию тока в цепи

Пишем уравнение для 1 – го контура

Это уравнение справедливо от

В этом интервале (1 квадрант)

Для другого контура

(2 – 3) Перанаправим i_r1 откуда

В интервале (2 – 3) опр Ud₁

Значениям t присвоем значения от до

В заштрихованных интервалах () интервалах токи нигде не протекают поэтому для определения Ud₁ в этих интервалах нужно пользоваться

Метод рассчета нелинейных цепей переменного тока по эквивалентным действующим заначениям

1 L U₂(U₁) - ? Nc r₂ U₁ U₂

2 C 3

r₂=10 Om 50 B

x_L=15 Om Uнс

x_C=10 Om 30 20 10 10 токов U₂ 0 1 2 3 5 Рассчет начнем с  точки нелинейной характеристики

(10) Umc = 50 B; I₁ = 5 A

0 U₁

Используем теоритеческие сведения полученные в разделе линейные электрические цепи переменного тока.

У r – эл – ть I экв действ U_экв знач – я переменного тока совпадает

У r – эл – ть I экв отстает от U_экв на 90’

У r – эл – ть I экв опережает U_экв на 90’

U₂

5 B

U₁

1 2

 I’₁ U_нс

I₂

U_c

3

B

По теореме cos найдем ток I