Методы анализа нелинейных цепей

1. Приближенные методы –метод основан на линеализации т. е. Замене нелинейных характеристик линейными (метод кусочно-линейной апраксимации, метод аналитической апроксимации)

Методы основаные на решении с-м ду с переменными параметрами

2. Метод математического моделирования

Цифровые методы (Метод Эйлера и Рунге-Кутта)

Пусть дана цепь

i

Д. u=Umsinwt, r, ВбАХ

U r О. i=0



2 +m 3

i

4 1

-m

U = ir +

L

1) t=0 (i)*1 (1-2)

i=0

U= =

Формула справедлива пока <=m

Найдем момент времени

t=0 (0)= -m =

c=

Определим момент времени t1 когда =+m

m= -

cos wt1=

wt1=arccos

При t>t1 рабочая точка перешла на участок (2-3)

= +m

Это решение будет справедливо до тех пор пока ток не станет рвным 0 (t=)

Рабочий ток на участке 2-1 i=0

c1=m-

t2-m=

wt2=arccos(2m-

При t>t2 уравнение такое же как при t

Т.е.

t



+m

t1 t2 t2 t

-m

t1  t2

2. Изменение аппроксимирующих формул



+m Пусть в некоторый момент времени t=t1

1 3 работа находиться в точке 1 (участок 1-2)

-i1 i

+i1

4 2 -m

См. § п-1 цепи на переменном напряжении в котором решение для точки имеет вид i=Ae^pt+i_n

= Sm(wt+_z)

-i1 = Sm(wt1+_z)

Пусть t1=0 тогда –i1= A sin _z

A = -i1- sin _z

Решение справедливо пока

t2 = ?

i1 = (-i1-

При t>t2 рабочий участок (2-3)

u=ir

t3 - ? i1 =

wt3 = arccos

u

t

• 2

+i1

t2 t1 t

t1 t2

-i1

Сравниваем 1) с 2)

2. Опишем гиперболической функцией

 ₂ 2

1

₁ Найдем  и  в двух точках

i₁ i₂

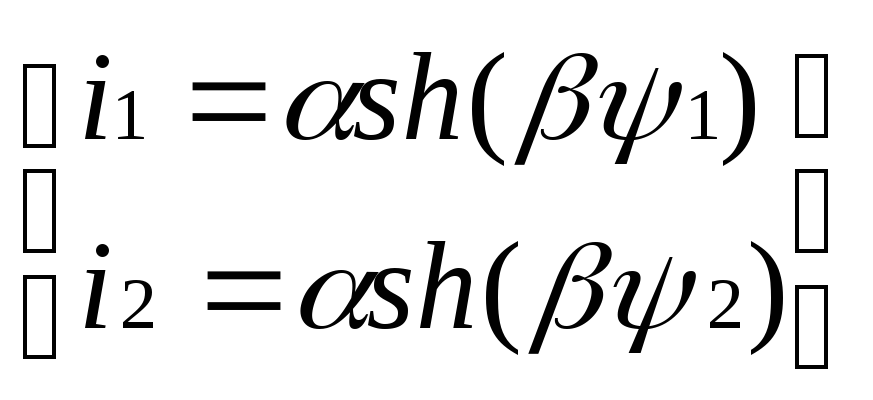
Вычислим  и зная i₁₂ и ₁₂

f()

k



₁ ₃ ₂

Аппроксимируем с помощью степенного ряда

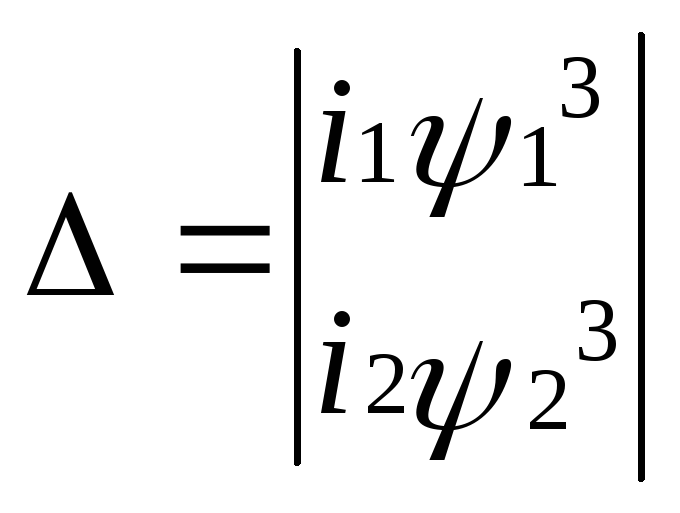
Нелинейное ДУ

Это ДУ решаем методом Эйлера

Р- м алгоритм реш-я методом Эйлера

2 Вар. Из функции найдем 

подставим в ДУ

- нелинейное

Решение методом Рунга-Кутта более точнее. Оно обеспечивает точность до 10^-4

Решение задачи анализа в нелинейных цепях методом математического моделирования

Метод основан на аналоговом моделировании процессов во временной области. Решение осуществляется с помощью решающих блоков, представлящих собой законченные электронные блоки выполняющие одну или несколько математических функций.

Для решения задачи необходимо:

1. Суммироване 

Умножение  (блоки осуществляющие перемножения)

Дифферинциаторы , интеграторы и функционалы

наб. блок аппроксимурующий нелинейность

+ ri=u u – ri ^



(i)

Главным решающим элементом является операционный усилитель у которого коэффициенты усиления u 10⁴ - 10⁶.

k=10⁴⁽⁶⁾

u₊₁ u₂

r обр.

r1 -u₁

u₁

1) Если при

если то k=1