Синтез эл. Цепей

Осн. Понятия и определения

Задачей синтеза считается обратимой задачей анализа

Если задача анализа однозначна то задачи синтеза нет и определяется тем что ее решает

Синтез

Синтез двухполюсников Синтез 4П

Синтез эл. Цепи

Синтез Синтез Синтез Синтез

ПДП АДП ПЧП АЧП

Задача синтеза : 1) По заданному операторному изображению либо эл. Величине

(ток, напряжение, мощность) определить эл. цепь. Реализующию это изображение.

1. По заданному отклику (переходному процессу )какой-либо эл. величины цепи восстановить эту цепь

Решение задач синтеза на базе теории переходных процессов.

u U₀

30

20

10

1 2 3 4 5 6 7 t x 10³

0. Опр-ть цепь и время п/п

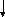
? U(t)

U

1)

r

U₀ L

Если r=10 Ом то Гн

2)

r

С U

I Т. к. нет скачка то в цепи есть L

Применяя теорию рассчитать п/п методом интеграла Дюамеля

Т t

Можно интегрировать воздейст F и эл. цепь

восстановив

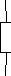
1

2 r₁ При t=T

U₀

Синтез пассивных эл. цепей

Условия Заданными будем считать или входное сопротивление или входную проводимость Если эти параметры заданы в операторном виде то научится по этим ф-ям находить эл цепь – вот это задача синтеза

(1)

r

L

Условия физической реализуемости пассивных цепей

Ф-ла (1) может быть реализована эл. цепью если ни один из коэф-ов числителя и занаменателя не равен отрицательному числу

а_к и b_к

Наивысшая степень при p в числители и в знаменатели не должна оличаться более чем на 1

Это же справедливо и для линейной степени

3) Полюсы ф-ии должны находиться в нежней части комплексной пл-ти т. е. действительных положительных корней нет

+1

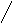
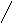
+j

Если корни лежат на мнимой оси то они не могут быть кратными

1. Нули ф-ии 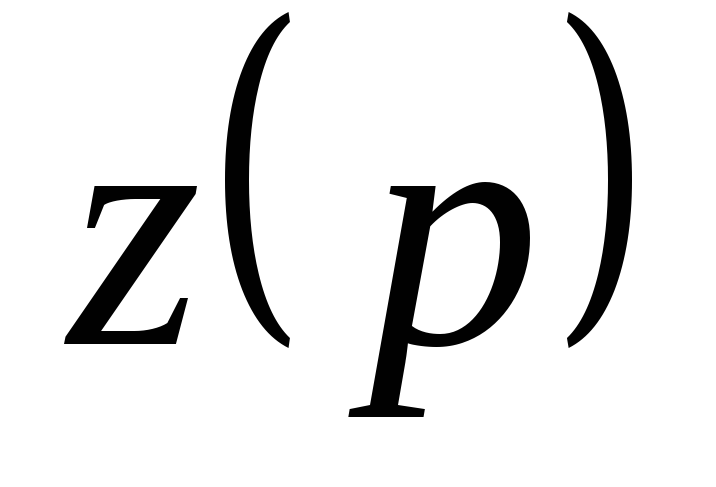так же должны находиться в нижней части комплексной пл-ти.

Причем ни один из корней полюса не может быть равен или кратен ни одному из корне нуля

5) Действит. Часть не должна быть меньше нуля

Если удовлетворяет всем этим условиям то она может быть реализована

Набор входных сопротивлений элементарных эл. цепей.

Если M(p)=0 то имеет нуль если то имеет полюс

r нет ни нулей ни полюсов эквивалентна r элементу

т. е. при p=0

в эл. цепи

L – элементы

Если в входном сопротивлении при некотором p есть 0 то следует ожидать в цепи L элемента

Если p=0 то L-эл-т точно есть в цепи

Если при ники-то p есть полное то в цепи с-эл-т

Если эл. цепь состоит только из реактивных эл-ов то полинома числителя и знаменателя содержат только четные или нечетные степени Причем если в числители четные то взаменателе нечетные и наоборот

Если таких эл-ов последовательно соедененных несколько то им можно представить суммой таких составляющих

Lp

Реализация пассивной эл. цепи способом последовательного выделения прстейших состовляющих

1. Пусть 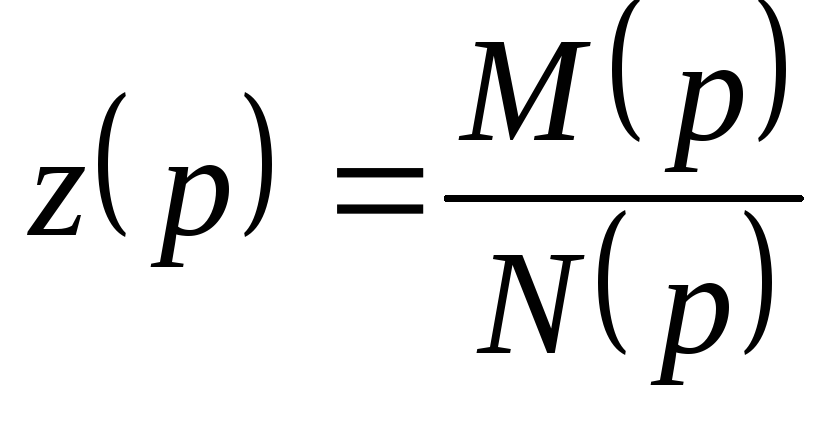задано и есть в

- индуктивность . Тогда оставшаяся

часть z может быть получена вычитанием из z(p) этой индуктивности

Если приесть р=0 то опять выделяют индуктивность

2) Ищем полюса

при р=0 то его выделяют

3) подвергают 1- му этапу а затем второму

Осуществляется до тех пор пока не будет не нулей ни полюсов

z(P)

a₁p 1/b₁p

z(p)

Проверяем есть ли комплексно сопряженные корни

то в эл. цепи есть параллельно соединенные L и C эл-ты

Если z(p) при этих корнях =0 то

при то

Повторяя описанные выше операции до тех пор пока оставшаяся часть не будет

Представлять собой элементарную схему которая и будет свидетельствовать об окончании синтеза. Такой способ называют метод Фостера

Пример 1

3) Полюс

2. Нули

3. 

1. +

2. +

3. + по пред прим

4. нуль

5. 

1. +

2. +

3. 

4. Нуль

1. Состоит только из LC эл-ов

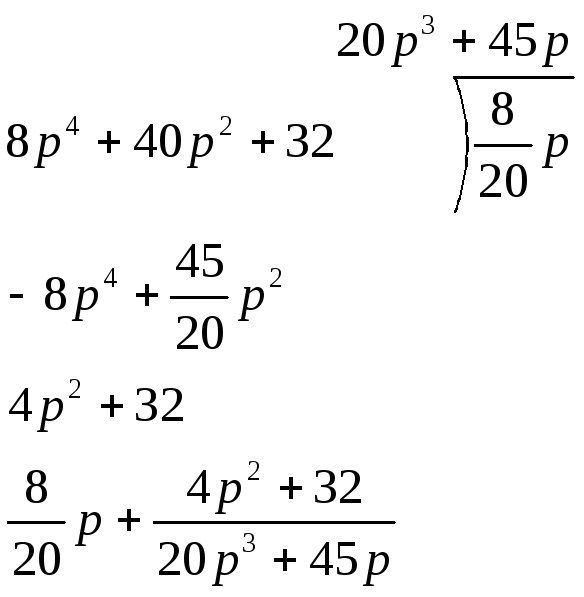
i1 r₂

i₃ U 1 e 2 r₁ 3 4 E₀

Находим контуры возможного протекания токов

Если вр интервал

е

Е₀

t₁ t₂

Когда сменяется полярность е то

Находим временной интервал

-е

- Е₀

i₂=

Т. к. u₂ и u₁ содержат одно проводящее состояние то u на них 0

Когда ток в них то их можно опр. Составлением ур-й неработающих контуров

Пишем ур-я для бестоковых интералов

все токи = 0

u₁

t

i₁ c₄ r₁

Ic

U1 r₂ x_L U₂ Uc

Uck

0 Ick k Ic

U₂

U_1k I_kr₁=Ur₁

0 U_1k U₁

U_nk

I_ck

U_ck U_lk

Ur₁

Метод Кауэра

Понятие о лестничной схеме двух-ка

z₁(p) z₃ z₅

z(p) y₂ y­­₄ y₆

Лестничная схема

1 +z₁=z(p)

1 +y₂

1 +z₃

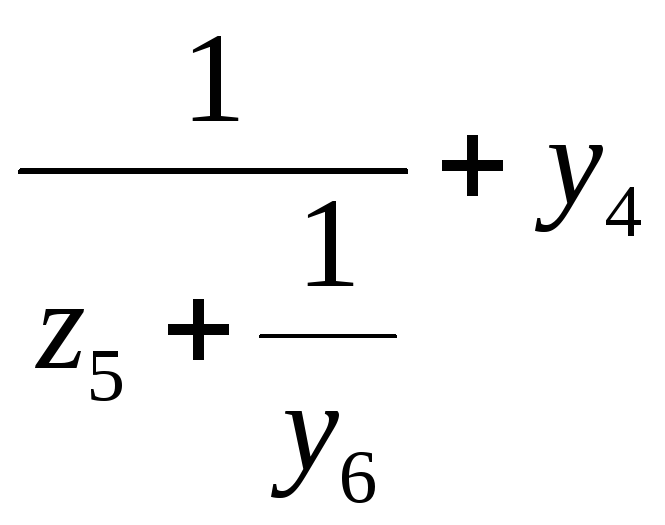
В методе синтезируют 2-х П- ки после выполнения условий Дирихле последовательным делением сначал числителя на знаменатель и в заключении как показано на схеме последо-но получают

и т. д.

Эта же лестничная структура может быть представлена и проводимостью

Разница будет в том что первой выделяемой эл-т проводимость

z₂ z₄

y₁ y₃ y­­₅