ГЛАВА ПЯТАЯ

Электрические фильтры

§ 5.1. Назначение и типы фильтров. Под электрическими филь­трами понимают четырехполюсники, включаемые между источником питания и приемником (нагрузкой), назначение которых состоит в том, чтобы беспрепятственно — без затухания — пропускать к приемнику токи одних частот и задерживать, или пропускать, но с большим затуханием, токи других частот.

Диапазон частот, пропускаемых фильтром без затухания, называют полосой прозрачности; диапазон частот, пропускаемых с затуханием, — полосой затухания.

Электрические фильтры собирают обычно из индуктивных катушек и конденсаторов. Исключение составляют RС - фильтры (см. § 5.6). Фильтры используют главным образом в радиотехнике и технике связи, где применяются токи довольно высоких частот.

При высоких частотах индуктивные сопротивления L индуктив­ных катушек во много раз больше их активных сопротивлений. Поэтому будем полагать, что активные сопротивления индуктивных кату щек и активная проводимость конденсаторов равны нулю, т. е. фильтры составлены только из идеальных реактивных элементов.

Фильтры обычно собирают по симметричной Т- или П - схеме (см, рис. 4.4, а, б), т. е. при Z2=Z1 и Z6=Z5.

При изучении фильтров будем пользоваться понятием о коэффи­циенте затухания и коэффициенте фазы (см. § 4.10).

Условимся сопротивления Z1 в схеме рис. 4.4, а и сопротивление Z4 в схеме рис. 4.4, б называть продольными сопротивлениями, а сопро­тивление Z3 в схеме рис. 4.4, а и сопротивления Z5 в схеме рис. 4.4, б— поперечными сопротивлениями.

Фильтры, в которых произведение продольного сопротивления на соответствующее поперечное сопротивление представляет собой неко­торое постоянное для данного фильтра число (число k), не зависящее от частоты, принято называть k-фильтрами. Фильтры, в которых это произведение зависит от частоты, называют т-фильтрами.

Сопротивление нагрузки Zн, присоединяемое на выходе фильтра, должно быть согласовано с характеристическим сопротивлением фильтра Zc. В k-фильтрах Zc существенно изменяется в зависимости от частоты , находящейся в полосе прозрачности. Это обстоятельство вызывает потребность изменять сопротивление нагрузки в функции от частоты (особенно при приближении к границе полосы прозрачности), что нежелательно. В т-фильтрах при определенных значениях коэф­фициента m, сопротивление Zc мало изменяется от частоты (в преде­лах полосы прозрачности) и потому нагрузка практически может быть одна и та же по величине для различных значений , находящихся в этих пределах.

Качество фильтра тем выше, чем более резко выражены его филь­трующие свойства, т. е. чем более резко возрастает затухание в по­лосе затухания.

Фильтрующие свойства четырехполюсников физически обусловлены возникновением в них резонансных режимов — резонансов токов или резонансов напряжений.

§ 5.2. Основы теории k-фильтров. Из § 4.10 известно, что если нагрузка Zн согласована с характеристическим сопротивлением Zc четырехполюсника, то напряжение U2 и ток в нагрузке I2 связаны с напряжением U1 и током I1 на входе четырехполюсника следую­щими соотношениями:

, где

Тогда

Множитель определяет, во сколько раз модуль напряжения (тока) на выходе фильтра меньше модуля напряжения (тока) на входе фильтра.

Если а = 0, то = = 1 и фильтр пропускает колебания без затухания. Таким образом, в полосе прозрачности а=0.

В полосе затухания а>0. Множитель , по модулю равный 1, свидетельствует о том, что напряжение U2 и ток I2 отстают соответ­ственно от U1 и I1 на угол b.

Фильтрующие свойства четырехполюсника рассмотрим путем срав­нения выражения для коэффициента А четырехполюсника с равным ему выражением гиперболического косинуса от аргумента а+jb:

A=ch(a+jb).

Гиперболический косинус от суммы двух аргументов (с учетом того, что ch jb = cos b и sh jb = j sin b) можно представить следующим образом:

ch (а + jb) = ch a cos b + j sh a sin b.

Для любого фильтра, собранного по Т-схеме (см. § 4.5), A=1 + (Z1/Z3).

Для фильтра, собранного по П -схеме (см. § 4.5), A=1+(Z4/Z5). Из каких бы реактивных сопротивлений ни был собран фильтр, отношение Z1/Z3 в Т-схеме и отношение Z4/Z5 в П- схеме всегда будет действительным (не мнимым и, не комплексным) числом—отношение двух мнимых чисел всегда есть число действительное.

Следовательно, всегда будет действительным и коэффициент А. Но если коэффициент A действителен, то действительным должно быть и выражение равного ему, ch (а+jb):

ch (а + jb) = ch а cos b + j sh a sin b = А.

Это выражение действительно, если

sh a sin b:=0. (5.1)

При этом

ch a cos b=A. (5.2)

Уравнения (5.1) и (5 2) используют для определения границ полосы прозрачности и характера изменения угла b в зоне прозрачности, а также характера изменения коэффициента затухания а в полосе (полосах) затухания.

Равенство (5.1) для полосы прозрачности (а=0) удовлетворяется, так как

sh a=sh 0=0. В силу того что ch 0=l, уравнение (5.2) для полосы прозрачности переходит в следующее: cos b=A. (5.3)

Круговой косинус (cos b) может изменяться в пределах от +1 до -1. Поэтому крайние значения коэффициента А [являющегося функцией частоты - A()] в полосе прозрачности равны ± 1. Полоса прозрачности в общем случае лежит в диапазоне частот от 1 до 2. Значения 1 и 2 для фильтров НЧ и ВЧ (подробнее см. § 5.3) определяют путем решения уравнений

A()==±1. (5.4)

Для полосовых и заграждающих фильтров (см. § 5.3) 1 и 2 находят как корни уравнения A()=-1. Для них уравнение A()=1 дает возможность определить так называемую резонансною частоту 0, находящуюся в интервале частот между 1 и 2.

Частоту, являющуюся граничной между полосой прозрачности и полосой затухания, называют частотой среза.

Характер изменения угла b в функции от  для зоны прозрач­ности определяют в соответствии с уравнением (5.3) следующим образом:

b= arccos A (). (5.5)

Определим a и b для полосы затухания. В полосе затухания а>0. Уравнение (5.1) удовлетворяется при условии

sin b=0, (5.6)

т, е. при

b=0 (5.7)

и (или) при

b=±. (5.8)

Согласно уравнению (5.2}, при b=0

ch a=A(), (5.9)

а при b= ± 

сh а=A(). (5.10)

Уравнения (5.9) и (5.10) позволяют по значениям А как функции w найти ch a в полосе затухания, а по ch a найти а и, таким образом, построить кривую а=f(). Из уравнений (5.7) и (5.8) следует, что в полосе затухания напряжение U2 на выходе фильтра находится либо в фазе (при b = 0), либо в противофазе (при b=± ) с напря­жением U1 на входе фильтра.

В заключение необходимо отметить два важных положения.

1. С изменением частоты  меняются коэффициенты В и С четы­рехполюсника, поэтому изменяется и характерисшческое сопротивле­ние Zc=B/C. Для того чтобы фильтр работал на согласованную нагрузку (только в этом случае справедлива изложенная здесь теория фильтров), при изменении частоты нужно менять и сопротивление нагрузки.

2. В полосе прозрачности характеристическое сопротивление филь­тра всегда активное, а в полосе затухания — чисто реактивное (индук­тивное или емкостное).

Если нагрузка фильтра не чисто активная или не согласована с характеристи­ческим сопротивлением фильтра или если требуется учесгь влияние активного сопротивления индуктивных катушек на работу фильтра (что существенно для низких частот), то для построения зависимости U1/U2=f () и зависимости угла сдвига фаз между U1 и U2 в функции частоты можно воспользоваться, например, методом пропорциональных величин (см &1.12). Характеристическое сопротивле­ние фильтра Zс берут равным внутреннему сопротивлению источника сигнала (генератора). При этом и генератор и фильтр работают в режиме согласования.

§ 5.3. К - фильтры НЧ и ВЧ, полосовые и заграждающие k-фильтры. Фильтрами НЧ (ФНЧ) называют фильтры, пропускающие в на­грузку лишь низкие частоты: с 1 = 0 до 2. Полоса их затухания находится в интервале от 2 до .

Схемы двух ФНЧ приведены на рис. 5.1, а, б. Характер измене­ния коэффициента затухания а и коэффициента фазы b качественно иллюстрируют кривые рис. 5.1, в.

Под фильтрами ВЧ (ФВЧ) понимают фильтры, пропускающие в нагрузку лишь высокие частоты: с 1 до . Полоса затухания их находится в интервале от 0 до 1.

Схемы двух ФВЧ приведены на рис. 5.2, а, б. Характер изме­нения коэффициентов a и b для них иллюстрируется кривыми рис. 5.2, в.

Рассмотрим вопрос об изменении величины характеристического сопротивления Zc в полосе прозрачности для Т-фильтра НЧ (см. рис. 5.1, а) и для Т-фильтра ВЧ (рис. 5.2, а), а также для П - фильтров. С этой целью в выражение Zc=B/C подставим значения В н С в соответствии с формулами (4.18) и проанализируем получен­ные выражения.

Для Т-фильтра НЧ (см. рис. 5.1, а)

При =1=0 Zc = . С увеличением частоты Zc уменьша­ется, сначала мало отличаясь от значения . При достижении значения =2= Zc=0.

Ряс. 5.1 Рис. 5.2

Для П-фильтра НЧ (см. рис. 5.1, б)

Для Т-фильтра ВЧ (рис. 5.2, а)

В этом случае характер изменения Zc отличен от характера изме­нения Zc для Т-фильтра НЧ, а именно:

Zc=0 при =1=1/. С увеличением w сопротивление Zc увеличивается и при   Zc=.

Для П-фильтра ВЧ (рис. 5.2, б)

Если фильтр предназначен для работы на частотах, находящихся внутри полосы прозрачности данного фильтра и относительно далеко отстоящих от значения , при котором Zc=0, то сопротивление нагрузки Zн на выходе фильтров НЧ выбирают равным Zc, которое соответствует =1=0. Для Т-фильтра НЧ (см. рис. 5.1, a) Zc =.

Для фильтров ВЧ обычно нагрузку согласовывают со значением Zc при . Для Т-фильтра ВЧ (рис. 5.2, a) Zc= . В по­лосе (полосах) затухания Zc оказывается чисто реактивным для всех типов k-фильтров.

Для того чтобы выяснить, индуктивный или емкостный характер имеет Zc в полосе затухания, следует определить характер входного сопротивления этого фильтра (фильтр всегда работает в режиме согласованной нагрузки) для пре­дельного режима, а именно:

Рис. 5.3 Рис. 5. 4

для фильтров НЧ (рис. 5.1, а, б) при очень высокой частоте, а для фильтров ВЧ (рис. 5.2, а, б) при очень низкой частоте (теоретически при 0), считая выходные зажимы схем закороченными. Тот же результат будет получен, если считать их разомкнутыми. В резуль­тате определим, что в зоне затухания Zc имеет индуктивный характер для Т-фильтра НЧ (см. рис. 5.1, а) и П-фильтра ВЧ (рис. 5.2, б) и емкостный характер для П-фильтра НЧ (см. рис. 5.1, б) и Т-фильтра ВЧ (рис. 5 2, в).

Полосовые фильтры представляют собой фильтры, пропускающие в нагрузку лишь узкую полосу частот от 1 до 2. Слева от 1 и справа от 2 находятся полосы затухания. Схема простейшего полосового k - фильтра изображена на рис. 5.3, а. Параметры схемы должны удовлетворять условию L1C1=L2C2.

Характер изменения а и b для полосового фильтра иллюстрируют кривые рис. 5 3, б.

Без вывода дадим формулы для определения параметров полосо­вого фильтра рис. 5 3, а по заданным частотам f1 и f2 и сопротивле­нию нагрузки фильтра Zc при резонансной частоте fр=wр/2:

1) fр =f1f2  2)С1=(f2-f1)/2f1f2Zc 3)L1=Zc/2(f2-f1) 4)C2=1/Zc(f2-f1)

5)L2=Zc(f2-f1)/4f1f2

Под заграждающими фильтрами, (рис. 5 4, а) понимают фильтры, в которых полоса прозрачности как бы разрезана на две части поло­сой затухания (рис. 5.4, б). Слева от 1 и справа от 2 находятся две части полосы прозрачности.

В схеме простейшего заграждающего фильтра на рис. 5.4, L1C1=L2C2

Обозначим р = 1/L1C1 и k=L1/L2 и запишем формулы для определения 1 и Zс фильтров рис. 5 3, а и 5 4, а.

Для рис. 5 3, а

для рис. 5 4, а.

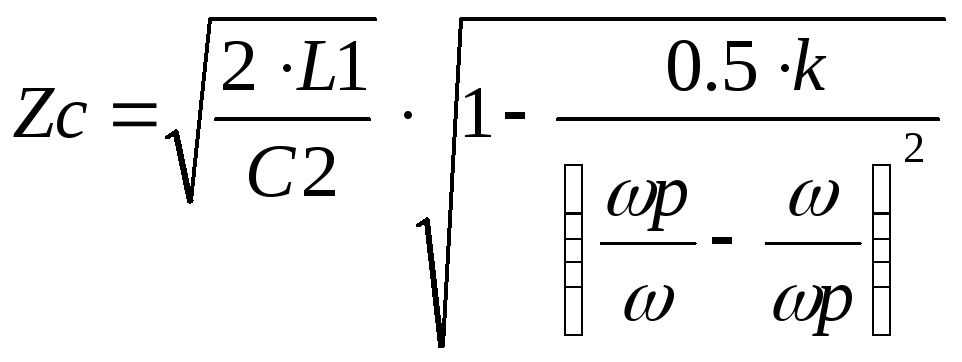
Для фильтра рис 5. 3, а в области частот от 0 до 1 Zс имеет емкостный характер, а в области частот от 2 до  - индуктивный. Для фильтра рис 5 4, а в области частот от 1 до 2 Zc имеет индуктивный характер, а в области от р до 2 – емкостный.

Характер изменения Zc иллюстрируется кривыми рис 5 3, а и 5 4, в

Пример 57. В схеме рис. 5. 1, а L = 10 мГ; С = 10 мкФ. Определить границы полосы прозрачности, закон изменения коэффициен­та a в полосе прозрачности, а также закон изменения коэффициента а в полосе затуха­ния, построить векторную диаграмму при  = 2000 рад/с и I2 = 0,2 А.

Р е ш е н и е. Для Т-схемы

Рис. 5.5 A=1+Z1/Z3=1+jLjC=1-LC.

При А = 1 1=0. При А = - 1 имеем -1=1-LC; отсюда 2= = 4470 рад/с.

В полосе прозрачности b=arccos A=arccos(l —LC).

При частоте  = 2000 рад/с, находящейся в полосе прозрачности,

Zc2L/C- =40 Ом. При нагрузке фильтра на характеристическое сопротивление напряжение на выходе U2= I2Zc = 0,2 • 40 = 8 В.

Напряжение на входе U1 также равно 8 В и опережает U2 на угол b = arccos 0,6  53° (рис. 5.5).

Для определения закона изменения а в полосе затухания (для дан­ного фильтра А отрицательно) используем уравнение

cha = -A=LC-1.

Найдем а, например, при =22= 8940 рад/с:

cha=(8940)² 10 ²10 ⁵-1=7; а=2,64 Нп.

Пример 58. Определить параметры полосового фильтра рис. 5.3, а, исходя из того, что он должен пропускать полосу частот от f1 = 750 Гц до f2 = 850 Гц и что сопротивление нагрузки Zн = Zc при резонансной частоте fр составляет 800 Ом.

Решение.

Гц Ф Гн

Ф Гн