Сравнивая (9.17) и (9.18), замечаем, что

Следовательно, для прохождения импульса или модулированного колебания через четырехполюсник без искажения формы необходимо,

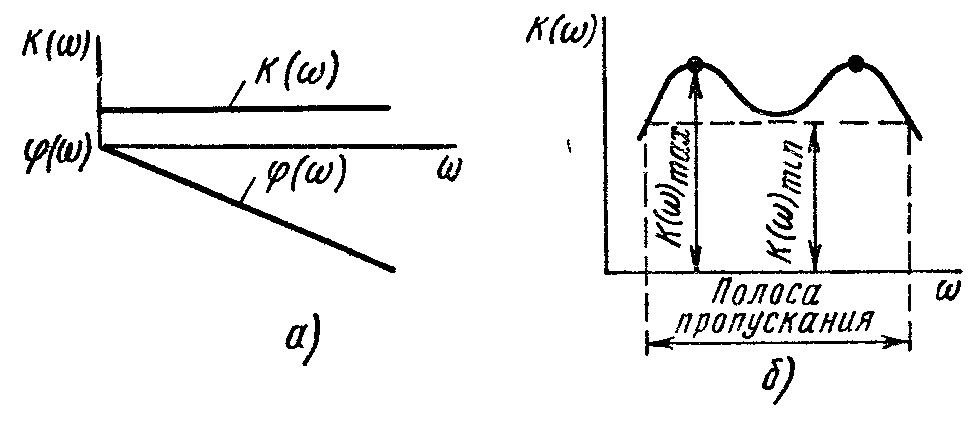
Рис 9.2

чтобы модуль передаточной функции четырехполюсника был постоянен (не зависел от частоты), а аргумент линейно изменялся в функции частоты (рис. 9.2, a).

В реальных четырехполюсниках эти условия могут быть выполнены лишь приближенно в некоторой полосе частот, которую называют по­лосой пропускания. Полоса пропускания ограничена значениями , при которых отношение максимального значения K() к минималь­ному равно (рис. 9.2, б). Такой характеристикой обладает, на­пример, схема рис. 3.42,а. Для этой полосы приближенно полагают, что K() = const и .

Для того чтобы сигнал при прохождении через четырехполюсник не изменил своей формы, необходимо, чтобы важнейшие гармонические составляющие частотного спектра сигнала находились внутри полосы пропускания четырехполюсника. Для импульсных сигналов треуголь­ной, трапецеидальной, прямоугольной, колоколообразной и некоторых других форм принимают, что они занимают полосу частот, грубо го­воря, от = 0 до , где - длительность импульса.

Так как в полосе пропускания идеальные условия для прохожде­ния импульса все же не выполняются, то, проходя через четырехпо­люсник, импульс в какой-то степени искажается Определить степень искажения можно двумя способами, основанными на частотных пред­ставлениях.

Первый способ состоит в непосредственном применении прямого и обратного преобразований Фурье.

Основные этапы этого способа таковы 1) нахождение спектра входного сигнала u₁(t); 2) определение передаточной функции четырех­полюсника K(j); 3) получение спектра выходного сигнала 4) определение u₂(t) пo

Последнюю операцию можно осуществить с помощью формулы (9 13), но практически ее удобнее выполнить, используя таблицу изображений по Лапласу, заменив j на p в

Такой путь решения мало чем отличается от решения той же за­дачи операторным методом и для сложных схем оказывается мало­пригодным, поскольку решение достаточно громоздко, и, пользуясь им, трудно сделать вывод о том, как тот или иной конкретный эле­мент схемы при неизменных остальных влияет на фронт импульса и на его вершину. Пользуясь этим методом, трудно также судить о том, какие элементы схемы в наибольшей степени влияют на деформацию фронта, какие—на деформацию вершины импульса.

В литературе по импульсной технике получил распространение второй способ решения, также основанный на спектральных представ­лениях. В основу его положено то обстоятельство, что искажение формы фронта выходного импульса по сравнению с формой фронта входного импульса зависит от свойств передаточной функции четырех­полюсника на высоких (теоретически на бесконечно больших частотах), а искажение вершины импульса определяется свойствами передаточ­ной функции на низких частотах (теоретически на частотах, близких к нулю).

Для того чтобы в этом убедиться, проделаем некоторые выкладки.

Взяв в качестве исходной формулу (8.63б) и заменив в ней вход­ное напряжение и(t) на и₁(t), ток i(t) на выходное напряжение че­тырехполюсника и₂(t), переходную проводимость g(t) на переходную функцию четырехполюсника h(t), получим

(9.19)

Положим, что напряжение и₁(t), подводимое в момент t=0 цепи с нулевыми начальными условиями, является синусоидальным и по амплитуде равно 1:

(a)

где 1 представляет собой комплексную амплитуду входного напряже­ния, т. е. Учтем, что

(б)

После подстановки (а) и (б) в формулу (9.19) получим

Комплексную амплитуду напряжения и₂(t) в установившемся синусоидальном режиме частоты  определим, если в квадратной скобке положим :

Передаточная функция четырехполюсника

(9.20)

При

(9.20')

Из формулы (9.20') следует, что свойства переходной функции четырехполюсника в начальный момент, т.е. h(0), определяются свойствами передаточной функции на бесконечно большой частоте . В свою очередь формула (9.21) свидетельствует о том, что свойства переходной функции при относительно больших моментах времени зависят от свойств передаточной функции при нулевой частоте

Таким образом, чтобы не исказился фронт импульса, следует обеспечить условия неискаженной передачи на высоких частотах, а для сохранения формы вершины импульса—условия неискаженной пере­дачи на низких частотах

Для того чтобы выяснить влияние отдельных элементов схемы на искажение формы импульса, прежде всего составляют полную схему замещения четырехполюсника, учитывая в ней все факторы, влияю­щие на частотные свойства [паразитные емкости ламп импульсных трансформаторов, индуктивности рассеяния трансформаторов, емкост­ные свойства p-n-переходов транзисторов, зависимость коэффициентов усиления транзисторов от скорости процесса (от частоты )].

Затем из полной схемы замещения образуют две расчетные схемы.

Первая схема представляет собой расчетную схему для высоких частот и служит для выяснения степени искажения фронта импульса. Эту схему получают из полной схемы замещения путем закорачивания последовательно включенных емкостей по пути следования сигнала (относительно больших по сравнению с паразитными) и разрыва индуктивностей, включенных параллельно активным сопротивлениям схемы.

Вторая схема представляет собой расчетную схему для. низких частот и служит для выяснения степени деформирования вершины импульса. Эту схему получают из полной схемы замещения, оставляя в ней последовательно включенные емкости по пути следования сигнала, а также индуктивности, включенные парал- ле льно активным сопротивлениям, и закорачивая последовательные индуктивности по пути следования сигнала. Паразитные емкости в низкочастотной схеме не учитывают.

В каждой из этих расчетных схем с учетом упрощений, о которых шла речь в § 8.16, число оставшихся индуктивностей и емкостей ока­зывается значительно меньше, чем в полной схеме замещения.

Для каждой из схем характеристическое уравнение оказывается часто первой или второй, сравнительно редко третьей степени, и по-

Рис. 9.3

этому влияние каждого из элементов схемы на искажение фронта и вершины импульса может быть выявлено относительно легко. Расчет переходного процесса в высокочастотной и низкочастотной схемах производят обычно операторным методом.

Окончательный результат (кривую всего переходного процесса) получают, сопрягая решения для этих двух схем. Вопрос об искаже­нии заднего фронта импульса принципиально решается так же, как и вопрос об искажении переднего фронта импульса.

Проиллюстрируем сказанное на примере. На рис. 9.3, а изобра­жена схема лампового усилителя на сопротивлениях, где —нагру­зочное сопротивление, — относительно большая разделительная емкость (через нее проходит только переменная составляющая выход­ной величины), — относительно малая емкость нагрузки и (или) емкость второго каскада усиления. Пунктиром показаны источник анодного напряжения и весьма малые по сравнению с (по не­сколько пикофарад) межэлектродные емкости , и (емкость анод—катод и емкость монтажа). В дальнейшем емкости , и не учитываем, как оказывающие малое влияние на работу схемы.

Схема замещения для расчета переходного процесса при воздей­ствии относительно малых по амплитуде переменных составляющих представлена на рис. 9.3, б. Она является схемой третьего порядка. Укороченные схемы для формирования фронта (рис. 9.3, в) и для формирования вершины импульса (рис. 9.3, г) являются схемами пер­вого порядка.

Для схемы рис. 9.3, в

где . Для схемы рис. 9.3, г

Если входное напряжение представляет собой прямоугольный импульс (рис. 9.3, д), то фронт выходного напряжения будет в виде нарастающей экспоненты (рис 9.3, е), а вершина—в виде спадающей экспоненты (рис 9 3, ж). Результирующая кривая изображена на рис. 9.3, з. Подбор параметров усилителя осуществляют исходя из допустимой деформации фронта и вершины выходного импульса по сравнению с входным импульсом.

§ 9.5. Определение переходной функции четырехполюсника через передаточную и передаточной через переходную. Если в формуле (9.20) заменить на , то передаточную функцию четырехполюсника на комплексной частоте найдем через переходную функцию следую­щим образом:

(9.22)

В свою очередь переходную функцию h(t) определим через пере­даточную , исходя из следующих соображений. В формуле для , заменив на комплексную частоту , получим . Выра­зим выходное напряжение четырехполюсника через входное и передаточную функцию

(а)

Так как h(t) есть выходное напряжение при , то, положив в (a) , получим

(9.23) ???????????????

Вопросы для самопроверки

1. Чем принципиально отличается ряд Фурье от интеграла Фypьe? Запишите и прокомментируйте формулы прямого и обратного преобразования Фурье.

2. Чем объяснить, что при обратном преобразовании Фурье кроме положительной угло­вой частоты со используется и отрицательная?

3. Любая ли функция f(t) может быть преобразована по Фурье?

4. Для функции f(t) известна F(р). Как запи­сать S(j) этой функции?

5. Построить графики модуля и аргумента спектров функций и 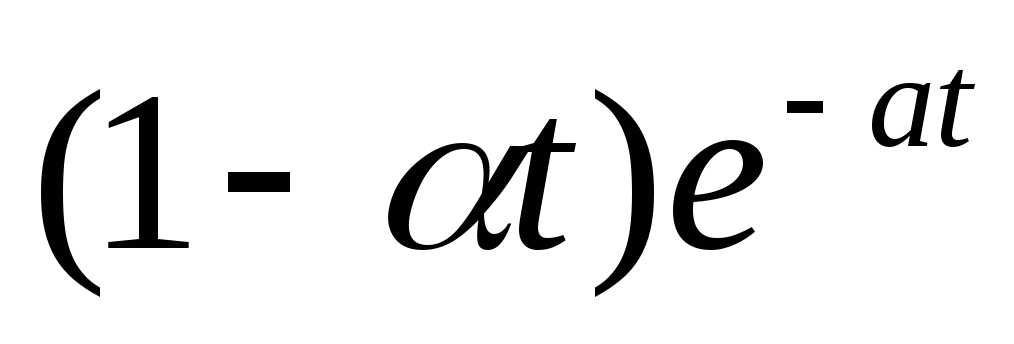(функции равны нулю при t<0)

6. Сформулируйте и докажите теорему Рейли, дайте ей физическое толкование.

7. Что понимают под полосой пропускания реального четырехполюсника?

8. Чем руководствуются при составлении укороченных схем четырехполюсника при исследовании дефор­мации фронта и вершины проходящего через него короткого импульса?

9. Как определить К(р) через h(t) и h(t) через К(p)?

10. Решите задачи 16.11, 16.35, 16.36, 16.41.