Новая папка / Примеры 7

Пример 75. Используя уравнение (8.8), составить характеристи­ческое уравнение для схемы рис. 8.4, а и найти его корни.

Решение.

или

Если дробь равна нулю, то равен нулю ее числитель. Следовательно,

(8.10)

Корни квадратного уравнения

В начале § 8.11 говорилось о том, что решение для свободного тока берется в виде Ае^pt. Если характеристическое уравнение имеет не один корень, а несколько, например n, то для каждого свобод­ного тока нужно взять

Пример 76. Найти корни характеристического уравнения схемы рис. 8.4, а при трех значениях С: 1) С=1 мкФ, 2) С =10 мкФ, 3) С ==100 мкФ, R₂=100 Ом; L₁=l Гн.

Решение. При С = 1 мкФ

При

При

Пример 77. Для схемы рис. 8.4, а входное сопротивление относительно зажи­мов аb при переменном токе

Заменим в нем j на р и приравняем его нулю:

Отсюда

или

(8.10`)

Уравнение (8.10') совпадает с уравнением (8.10), составленным иным путем. Уравнение (8.10') получено путем использования выражения для входного сопротивления первой ветви схемы рис. 8.4, а относительно зажимов аb. Точно такое же уравнение можно получить, если записать выражение для входного со­противления любой другой ветви.

Пример 78. Убедиться в том, что для схемы рис. 8.5 характери­стическое уравнение имеет не четвертую, а третью степень.

Решение. Составляем выражение для входного сопротивления:

Отсюда

Следовательно, характеристическое уравнение имеет третью степень.

Рис. 8.5

Рис. 8.6

Рис. 8.16

.

Пример 79. Выяснить, можно ли ожидать возникновения электрической искры (дуги) при размыкании ключа в схеме рис 8.16

Решение До размыкания ключа в цепи был остановившийся режим:

Допустим, что при размыкании ключа искра не возникает. При этом ток почти мгновенно спадает до нуля, а должен будет равняться . Но каждый из токов () по первому закону коммутации не может измениться скачком.

Следовательно, между достаточно медленно расходящимися контактами ключа в схеме рис 8 16 при определенных условиях можно ожидать возникновения электрической искры (дуги). Расчет переходного процесса в схеме рис. 8.16 см. в § 8.28.

Пример 80. К зажимам индуктивной катушки R=100 Ом, L=10 Гн под­ключен вольтметр (рис. 8.17). Сопротивление вольтметра R_V=3000 Ом, E==100 В. Приближенно найти напряжение на зажимах вольтметра при t=0, если допу­стить, что размыкание ключа произойдет мгновенно и искры не возникнет.

Решение. До размыкания ключа через L проходит ток . В индуктивности была запасена магнитная энергия Если допустить, что размыкание ключа произошло мгновенно и искры не возникло, и учесть, что ток через индуктивность должен оставаться равным 1 А, то по замкнутому контуру, составленному вольтметром и катушкой, за счет запаса энергии магнитного поля индуктивности в первое мгновение будет проходить ток в 1 А. При этом на вольтметре возникнет пик напряжения порядка 3000 В. Прохождение большого импульса тока через вольтметр может вызвать перегорание катушки прибора и выход его из строя.

При размыкании ключа с конечной скоростью между его расходящимися контактами (рис. 8.17) возникнет электрическая искра (дуга). Это приведет к тому, что увеличение напряжения на вольтметре бу­дет меньше, чем в только что рассмотренном идеализированном случае, когда ключ размы­кался мгновенно без искры (дуги) ¹.

Чтобы не «сжечь» вольтметр в цепи рис. 8.17, сначала надо отключить вольтметр, а за­тем разомкнуть ключ.

Рис. 8.17

Перенапряжения проявляются тем сильнее, чем больше индуктивности в цепях. Особенно опасны они в цепях постоянного тока, содер­жащих индуктивности порядка единиц и десят­ков генри. В таких цепях при отключениях соблюдают специальные меры предосторожности (отключение ключа после введе­ния дополнительных активных сопротивлении в цепь).

Пример 81. В схеме рис. 8.18 до замыкания ключа был установившийся режим:

Требуется: 1) найти полные, принужденные и свободные составляю­щие токов при t = 0₊, а также начальное значение производной от свободного напряжения на емкости; 2) определить токи и напряжение в функции времени.

Решение первой части задачи.

До коммутации

и .

Напряжение на емкости равнялось напряжению на сопротивле­нии R₃:

Найдем принужденные значения токов и напряжений после ком­мутации:

По второму закону Кирхгофа составим уравнение для контура, образованного первой и второй ветвями при t=0₊:

Поэтому

Из уравнения

получим

По первому закону Кирхгофа,

Следовательно,

Свободные составляющие тока и напряжения определим как раз­ности между полными и принужденными величинами.

Так как свободный ток через емкость,

то

В рассматриваемом примере

Решение второй части задачи.

Характеристическое уравнение для после коммутационной схемы имеет один корень

Каждый ток равен сумме принуж­денной составляющей и свободной состав­ляющей Ае^pt, где А равно значению сво­бодной составляющей при t=0₊ (рис. 8.19):

Рис 8.19

Рис. 8.20

Пример 82. В схеме рис. 8 20 до замыкания ключа был устано­вившийся режим: R₁=R₂==2 Oм, L==3 Oм, e(t)== 127 sin (t— 50°) В, =314 с ^–1.

Требуется: 1) найти ; 2) определить закон изменения тока в цепи после коммутации.

Решение первой части задачи.

Комплексная амплитуда тока в цепи до коммутации

Мгновенное значение тока до коммутации

В момент коммутации (при t = 0)

Принужденный ток после коммутации

Мгновенное значение принужденного тока

По первому закону коммутации,

Но

Следовательно,

Решение второй части задачи.

Характеристическое урав­нение имеет корень

По данным первой части задачи, ток в цепи до коммутации (кри­вая 1 рис. 8.21 до (t=0)

Мгновенное значение принужденного тока после коммутации (кри­вая 2 рис. 8.21)

Следовательно,

Кривая 3 рис. 8.21 определяет характер изменения свободного тока, кривая 4— полного тока после коммутации (ординаты кривой 4 при t 0 равны сумме ординат кривых 2 и 3).

Пример 83. В схеме рис. 8.22 ключ замыкается в третьей ветви. До этого был установившийся режим: e(t)=E=120 В. Требуется найти: 1)

2)

Решение первой части задачи.

До замыкания ключа

Принужденный ток после коммутации

Постоянный ток через емкость не проходит, поэтому

От постоянного тока на индуктивности нет падения напряжения, следовательно,

Рис. 8.21

Рис. 8.22

Принужденное напряжение на емкости равно падению напряжения

на сопротивлении R₂ от тока t_2пр:

По первому закону коммутации,

Но

откуда

или

Составим уравнение по второму закону Кирхгофа для замкнутого контура, образованного первой и третьей ветвями:

Так как

то

Найдем :

Чтобы определить составим уравнение для свободных составляющих по контуру, образованному первой и второй ветвями:

откуда

Но

Следовательно,

Свободное напряжение на емкости при подсчитаем по вто­рому закону коммутации:

отсюда

Определим скорость изменения свободной составляющей напряже­ния на емкости при .

С этой целью воспользуемся тем, что

Следовательно,

Решение второй части задачи.

Характеристическое урав­нение

имеет два комплексно-сопряженных корня:

Поэтому свободная составляющая должна быть взята в виде

где  = 42,1; ₀ =15,2; А и  определяют по значению свободной со­ставляющей и ее первой производной при t=0₊.

По данным первой части задачи,

i_2пр = 2 А; i_2св(0₊) = 0; i`_2св(0₊) == -5 А/с;

u_Cпр = 20 В; u_Cсв(0₊) = -20 В; u`_Cсв(0₊)=1333 В/с.

Функцияпри t =0 равна . Производная функции равна

Значение этой производной при t=0 равно

Найдем значения А и  для свободной составляющей тока i₂. Для этого составим два уравнения:

или Asin=0;

, или

Совместное решение их дает  = 0 и А = -0,328 А.

Следовательно,

Кривая 1 рис. 8.23 выражает собой график .

Найдем А и  для свободной составляющей напряжения :

или A sin  = -20;

, или

Отсюда А =37,9 и  = -31°52'.

Та­ким образом,

Кривая 2 рис. 18.23 изображает u_С = f(t).

Пример 84. В схеме рис. 8.22 e(t)^ == 127 sin (314t + 40°) В. Параметры схе­мы те же, что и в примере 83. До вклю­чения ключа в схеме был установивший­ся режим: u_C(0_-) = 0.

Рис. 8.23

Требуется найти:

1)

2)

Решение первой части задачи.

До коммутации

Определим принужденные токи и напряжения на емкости после коммутации.

Входное сопротивление цепи

тогда

Мгновенное значение принужденного тока после коммутации

Комплексное сопротивление параллельно соединенных второй и третьей ветвей

Комплексное напряжение на параллельном участке

отсюда

Мгновенные значения принужденных токов после коммутации:

Принужденное напряжение на емкости

Мгновенное значение принужденного напряжения на емкости после коммутации

По первому закону коммутации,

Свободное напряжение на емкости найдем по второму закону коммутации:

Для определения составим уравнение по контуру, образо­ванному первой и третьей ветвями:

Заменим в нем на [—0,0487 + ] и, учтя, что

получим:

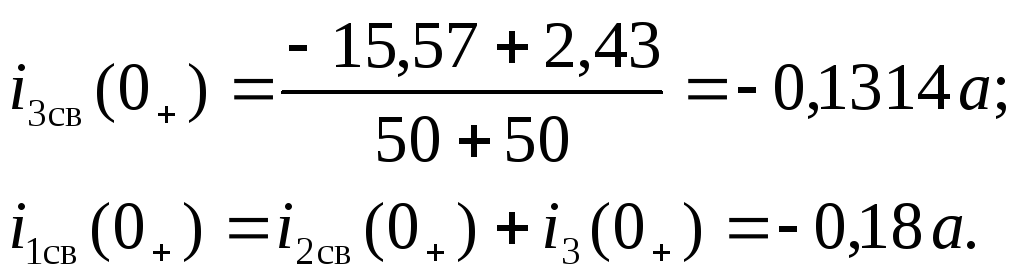
Чтобы определить

составим уравнение для контура, образованного первой и второй ветвями:

откуда

Решение второй части задачи.

По данным, полученным при решении первой части,

Корни характеристического уравнения те же, что и в предыдущем примере. Определим А и  для , составив два уравнения:

откуда А = 0,184 a и  = 15°20'.

Следовагельно,

Найдем А и  для составив два уравнения:

Их совместное решение дает А = 21,3 и  = 136°50'.

Пример 85. Послекоммутационная схема рис. 8.16 имеет всего один контур. По первому закону (правилу) коммутации,

Закон изменения тока при t  0, если считать, что до коммутации был установившийся режим,

Пример 86. Для схемы рис. 8.24 известны . По второму закону (правилу) коммутации составляем одно уравнение (т. е. столько, сколько надо составить уравнений для после коммутационной схемы по первому закону Кирхгофа):

отсюда

При t  0₊

Характер изменения и , показан на рис. 8.25, а и б. R заключение обратим внимание на то, что, допустив при переходе от t = 0_- к t = 0₊ скачкообразное изменение токов через индуктивно­сти и скачкообразное изменение на­пряжений на емкостях, тем самым допускаем скачкообразное измене­ние энергии магнитного поля индуктивностей и энергии электриче­ского поля емкостей.

Суммарная энергия электриче­ского и магнитного полей при t = 0₊

всегда меньше суммарной энергии при t = 0_- , так как часть запасенной энергии расходуется на тепловые потери в сопротивлениях, искру при коммутации, электромагнитное излучение в окружающее пространство.

Рис. 8.25

6.1* Рассчитать переходной процесс в цепи рис.6.1.

если U₀=100 В; U_c(0)=40 B; r=100 Ом; С=100 мкФ

Построить графики напряжения на конденсаторе

U_c(t) и тока в цепи- i(t).

Решение: Дифференциальное уравнение , описывающие переходной процесс в рассматриваемой цепи, имеет вид:

ir+U_c=U₀

Так как ток , то

Это неоднородное дифференциальное уравнение первого порядка. Его решение ищем в виде:

U_c=U_{c пр}+U_{c св}=U_{с пр}+Аe^pt.

где U_{с пр} - принужденная составляющая напряжения на емкости;

U_{с св} - свободная составляющая напряжения;

А - постоянная интегрирования;

p-корень характеристического уравнения.

Характеристическое уравнение имеет вид:

Crp+1=0

Его корень равен: p= -1/rC= -1/(10^{2 .}10^-4)= -100 1/c.

Принужденное значение напряжения на конденсаторе :

U_{с пр}=U_o=100 B.

Постоянную интегрирования находим из уравнения, составленного для момента времени t=0₊ (сразу после замыкания ключа).

U_c(0)=U_{c пр}(0)+U_{с св}(0);

40=100+A;

A=-60 B.

Уравнение для напряжения на конденсаторе имеет вид:

U_C(t)=100 - 60e^-100t, B.

Ток через конденсатор:

Г рафики тока и напряжения на емкости представлены на рис. 6.2.

Рассчитать все токи и напряжения на конденсаторе в цепи (рис. 6.7). Входное напряжение =30 В; r=100 Ом; С=100мкФ.

Решение:

Система дифференциальных уравнений для цепи после коммутации имеет вид:

Сводим систему к одному уравнению. За неизвестную величину примем , так как напряжение на ёмкости подчиняется законам коммутации:

;

Учитывая, что , получаем дифференциальное уравнение с одним неизвестным: ;

Характеристическое уравнение имеет вид:

.

Его корень: .

Решение дифференциального уравнения имеет вид:

;

где принуждённое значение напряжения на ёмкости равно:. .

Постоянную интегрирования A ищем из уравнения, записанного для t=0.

; ; 30=20+A;

A=10 B.

Решение для напряжения на конденсаторе:

, В.

Ток через конденсатор:

А;

Ток можно найти по закону Ома:

, А;

Ток в неразветвлённой части цепи определяется по первому закону Кирхгофа: , А;

Следует отметить, что избранный метод не является наилучшим с точки зрения трудозатрат. Эту же задачу можно решить проще, используя метод входного сопротивления, позволяющий получить характеристическое уравнение, не составляя системы дифференциальных уравнений. Рассмотрим, как это сделать.

Запишем комплексное входное сопротивление цепи после коммутации:

Заменим j на р:

Приводим дробь к общему знаменателю:

;

Приравниваем Z(p) к нулю, при этом числитель дроби будет равен нулю:

2rpC+3=0.

Мы получили характеристическое уравнение. Дальнейшее решение задачи проводится также, как показано выше.

Метод входного сопротивления целесообразно применять всегда, когда цепь достаточно сложна и, особенно, если она содержит два реактивных элемента и более.

Найти ток в индуктивности, если: .

Схема электрической цепи показана на рис. 6.11.

Решение: Эту задачу целесообразно решать путём сведения к нулевым начальным условиям.

Определим напряжение на разомкнутом ключе: