§ 8.18. Характер свободного процесса при одном корне.

Когда характеристическое уравнение имеет один корень, свободный ток

(8.12)

где зависит только от параметров цепи, А – от параметров цепи, э. д. с. и момента включения. Характер измененияt_свпри А >0 показан на рис. 8.8.

За интервал времени функцияуменьшится в е = 2,71 раза. Действительно, при

Величину принято называть постоянной времени цепи⁴;зависит от вида и параметров схемы. Так, для цепи рис. 8.2, для цепи рис. 8.3, а, (для цепи рис. 8.18) и т.д.

§ 8.19. Характер свободного процесса при двух действительных неравных корнях.

Пусть Для определенности положим b>а; тогда

(8.12а)

Характер изменения свободного тока при различных по величине и знаку постоянных интегрирования А₁и А₂качественно иллюстри­руется кривыми рис. 8.9, а—г; кривая 1 представляет собой функ­цию; кривая 2— функцию; результирующая («жирная») кривая получена путем суммирования ординат кривых 1 и 2.

Для рис. 8.9, a A₁>0 и A₂>0;

для рис. 8.9, б A₁>0, А₂<0,;

для рис. 8.9, в

для рис. 8.9, г A₁>0, A₂<0,

§ 8.20. Характер свободного процесса при двух равных корнях.

Известно, что если среди корней характеристического уравнения есть два равных корня р₁= р₂=-а, то соответствующие слагаемые реше­ния должны быть взяты в виде

(8.13)

На оис 8 10 построены пять кривых. Они показывают возмож­ный характер изменения функции при различных зна­ках постоянных интегрирования А₁и А₂, а также когда одиа из постоянных равна нулю.

Кривая 1 при A₁>0 и А₂>0;

кривая 2 при A₁<0 и А₂>0;

кривая 3 при A₁>0 и A₁<0;

кривая 4 при A₁=0 и А₂>0;

кривая 5 при A₁>0 и А₂=0.

§ 8 21. Характер свободного процесса при двух комплексно-со-пояженных корнях.

Комплексные корни всегда встречаются попарно сопряженными.

Рис. 8.9.

Так, если , то другой

Соответствующее им слагаемое решения долж­но быть взято в виде

(8.14)

Формула (8.14) описывает затухающее сину­соидальное колебание (рис. 8.11) при угловой частоте ₀и начальной фазе. Огибающая ко­лебания определяется кривой Ае^-t. Чем боль­ше, тем быстрее затухает колебательный про­цесс; A иопределяются значениями пара­метров схемы, начальными условиями и величи­ной э. д. с. источника;₀изависят только от параметров цепи после коммутации;₀назы­вают угловой частотой свободных колебаний;

 - коэффициентом затухания.

§ 8.22. Некоторые особенности переходных процессов.

Как известно из предыдущего, пол­ное значение любой величины (тока, напряже­ния, заряда) равно сумме принужденной и сво­бодной составляющих. Если среди корней харак­теристического уравнения есть комплексно-соп­ряженные корни и значение угловой частоты свободных колебаний₀почти роено угловой частоте со источника синусоидаль­ной э. д. с. (источника питания), а коэффициент затуханиямал (цепь с малыми потерями), то сложение принужден­ной и свободной составляющих дает колебание, для которого харак­терно биение амплитуды (рис. 8.12).

Колебание рис. 8.12 отличается от колебаний, рассмотренных в § 7.14, тем, что здесь у одной из составляющих колебания ампли­туда медленно уменьшается.

Если угловая частота свободных колебаний ₀ в точности равна угловой частоте источника синусоидальной э. д. с. , то результирую­щее колебание имеет форму, изображенную на рис 8.13.

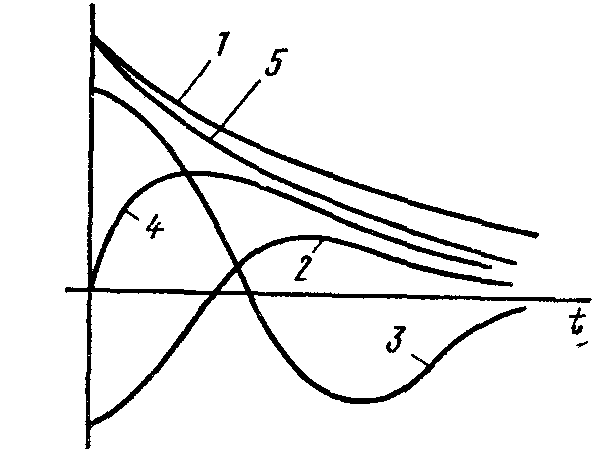
Рис. 8.10

Рис. 8.11

Простейшим примером колебаний такого типа является колебание возникающее на емкости в схеме рис. 8.14 в результате сложения принужденного колебания l/c„cos<o^ и свободного колебания и свободоного колебания

Рис. 8.12

Рис. 8.13

Амплитуда результирующего колебания нарастает по экспоненци­альному закону.

Рис. 8.14

Рис. 8.15

При наличии емкости (емкостей) в схеме могут возникать большие начальные броски токов, в несколько раз превышающие амплитуды тока установившегося режима. Так, в схеме рис. 8.15 при нулевых начальных условиях в первый момент после замыкания ключа напря­жение на емкостях равно нулю и ток в неразветвленной части цепи равен. Если=90°, то в первый момент после замыка­ния ключа ток равен. При размыкании ключа в индуктивных цепях возникают опасные увеличения напряжения на отдельных участках цепи (см. § 8.24).