§ 8.12. Составление характеристического уравнения системы.

Число алгебраических уравнений равно числу неизвестных свободных токов. Положим, что р известно (в действительности оно пока не най­дено и будет определено в дальнейшем) и решим систему (8.8) отно­сительно .Получим:

где — определитель системы. В рассмотренном примере

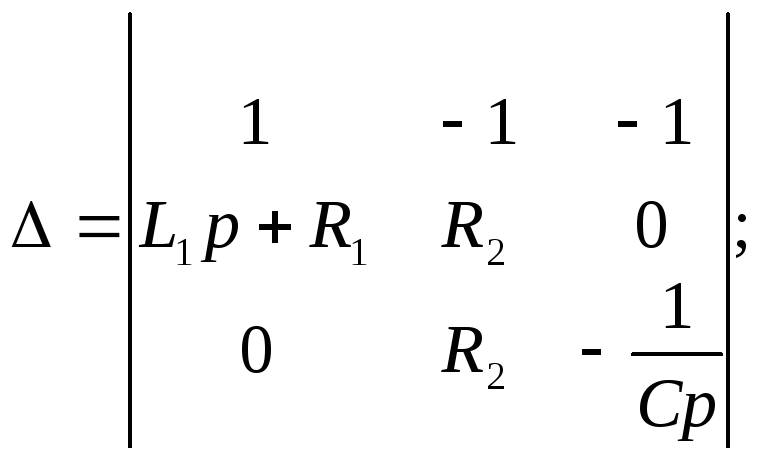
Определитель ₁получим из выражения для определителя Л путем замены первого столбца правой частью уравнений (8.8):

определитель ₂получим из выражения дляпутем замены второго столбца правой частью системы (8.8), и т. д.

Так как в правой части системы (8.8) находятся нули, то в каждом определителе ₁,₂и₃один из столбцов будет состоять из нулей.

Известно, что если в определителе один из столбцов состоит из нулей, то этот определитель равен нулю. Следовательно, ₁=0;₂=0;₃=0.

Из физических соображений ясно, что каждый из свободных токов не может быть равен нулю, ибо в этом случае не будут выполнены законы Коммутации. Однако из предыдущего следует, что

Свободные токи могут быть не равны нулю в том случае, если определитель системы

 = 0. (8.9)

При этом каждый из токов представляет собой неопределенность

раскрыв которую можно полу­чить действительное значение каждого свободного тока.

Раскрытием неопределенностей заниматься не будем, а восполь­зуемся тем существенным для дальнейшего выводом, что определитель алгебраизированной системы уравнений должен равняться нулю.

Уравнение = 0 называют характеристическим уравнением. Един­ственным неизвестным в нем является р.

Пример 75. Используя уравнение (8.8), составить характеристи­ческое уравнение для схемы рис. 8.4, а и найти его корни.

Решение.

или

Если дробь равна нулю, то равен нулю ее числитель. Следовательно,

(8.10)

Корни квадратного уравнения

В начале § 8.11 говорилось о том, что решение для свободного тока берется в виде Ае^pt. Если характеристическое уравнение имеет не один корень, а несколько, напримерn, то для каждого свобод­ного тока нужно взять

Пример 76. Найти корни характеристического уравнения схемы рис. 8.4, а при трех значениях С:1) С=1 мкФ, 2) С =10 мкФ, 3) С ==100 мкФ, R₂=100 Ом; L₁=l Гн.

Решение. При С = 1 мкФ

При

При

§ 8.13. Составление характеристического уравнения путем исполь­зования выражения для входного сопротивления цепи на перемен­ном токе. Характеристическое уравнение для определения р часто составляют более простым способом, чем обсуждавшийся в предыду­щем параграфе. С этой целью составляют выражение входного сопро­тивления двухполюсника на переменном токе [обозначим его Z(j)], заменяют в немjна р[получаютZ(p)] и приравниваютZ(p)нулю.

Уравнение Z (р) = 0совпадает с характеристическим. Такой способ составления характеристического уравнения предполагает, что в схеме отсутствуют магнитносвязанные ветви. Если же магнитная связь между ветвями имеется, то предварительно следует осуществить раз­вязывание магнитносвязанных ветвей.

В § 8.41 показано, что число р можно представить в виде j, где - комп­лексная угловая частота;Z (р)есть сопротивление цепи на комплексной частоте. Сопротивление цепи для синусоидального тока частотой а, т. е.Z (j),есть частный случайZ(p),когда =.

Входное сопротивление на комплексной частоте по отношению к некоторой k-й ветви , где(р) — определитель системы уравнений, составлен­ных по методу контурных токов;_k(р)—алгебраическое дополнение.

Корни уравнения Z_k(р) = 0совпадают с корнями уравнения(р)=0.

Следует иметь в виду, что во избежание потери корня (корней) нельзя сокра­щать (р) и_k(р) на общий множитель, если он имеется.

И последнее замечание: при составлении Z (р)следует учитывать внутреннее сопротивление источника питания.

Характеристическое уравнение можно составлять также, приняв за основу при. его составлении не метод контурных токов, а метод узловых потенциалов. В этом случае следует приравнять нулю определитель матрицы узловых проводи-мостей, полагая при составлении матрицы один из узлов схемы заземленным.

Пример 77. Для схемы рис. 8.4, а входное сопротивление относительно зажи­мов аb при переменном токе

Заменим в нем j'o на р и приравняем его нулю:

Отсюда

или

(8.10`)

Уравнение (8.10') совпадает с уравнением (8.10), составленным иным путем. Уравнение (8.10') получено путем использования выражения для входного сопротивления первой ветви схемы рис. 8.4, а относительно зажимов аb. Точно такое же уравнение можно получить, если записать выражение для входного со­противления любой другой ветви.