Новая папка / Примеры решения 54

Пример 54. Построить геометрическое место концов вектора тока неразветвленной части схемы рис. 4.16 и графически исследовать воз­можность возникновения резонансных режимов при следующих дан­ных: =30 В; R2=6 Ом; Хс=8 Ом; R1=3 Ом; XL изменяется от 0 до .

Решение. Ток в схеме остается неизменным:

Ток на 53°10' опережает э. д. с. (рис. 4.17). Вектор тока пои изменении XL меняется так, что конец его скользит по дуге

Рис. 4.16

окружности, диаметром которой являет­ся вектор тока

Ток в неразветвленной части схемы . Геометрическим местом его является также дуга окружности а12b. В режимах, соответствующих точкам 1 и 2, ток совпадает по фазе с э. д. с. . Следовательно, в этих режимах в схеме имеет место резонанс токов.

Выберем масштаб сопротивлений mZ=2 Ом/см . Графически найдем XL для точек 1 и 2. Для точки 2 XL0.8 Ом, для точки 1 XL 10,6 Ом. При этом ток I=11,1 А и 2,4 А.

Пример 55. Построить круговую диаграмму тока схемы рис. 4.18, о, в ко-торой XC=5 Ом; R=5 Ом; E=100 В. Нагрузкой четырехполюсника является индуктивное сопротивление ХLкоторое может изменяться от нуля до бесконеч­ности.

Решение. Найдем ток холостого хода выходная ветвь разомкнута):

Определим ток короткого замыкания (при коротком замыкании нагрузки):

Рассчитаем входное сопротивление Z2k со стороны зажимов pq при коротком

замыкании зажимов тп:

Следовательно, . Угол .

Круговая диаграмма тока построена на рис. 4 18, б. Хордой оуружности является разность . Угол , поэтому для определения положения касательной он отложен от продолжения хорды против часовой стрелки. Диаг­рамма носит несколько необычный характер: рабочая часть дуги занимает почти целую окружность.

Для определения положения конца вектора тока из конца вектора через точку на линии XL, соответствующую заданной величине XL, проводится прямая до пересечения с рабочей частью дуги окружности. При XL=5Ом ток опе­режает э. д. с. на 90°.

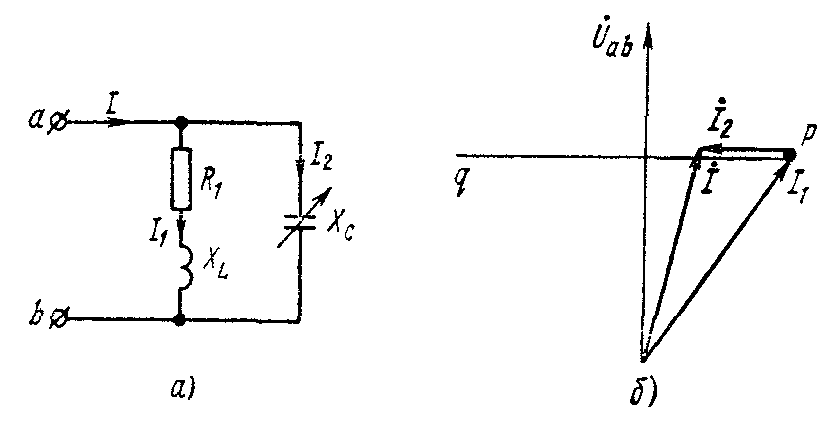
Пример 56. Построить геометрическое место кон­цов вектора тока в схеме рис. 4.19, а при изменении Хс. Напряже­ние =const, R1 и XL неизменны.

Решение. На рис. 4.19, б изображаем вектор . Вектор тока I отстает от него на угол  = arctg XL/R1,

Ток опережает на 90°. Геометрическим местом концов тока будет прямая линия pq. Она и является линейной диаг­раммой тока .

Пример 59. В схеме рис. 6.12, а э. д. с. каждой фазы трехфазного генератора равна 127 В. Сопротивления фаз нагрузки равны по вели­чине (6,35 Ом), но имеют различный характер:

.

Определить ток в нулевом проводе.

Решение. Построим векторную диаграмму (рис. 6.12, б). Токи всех фаз по модулю равны .

Рис. 6.12

Ток совпадает по фазе с . Ток на 90° отстает от . Ток опере­жает на 90°. Сумма дает век­тор тока . По модулю он равен 14,6 А.

Пример 60. Какой величины должно быть взято сопротивление R в фазе А схемы рис. 6.12, а, чтобы ток в нулевом проводе стал рав­ным нулю?

Рис.6.1

Решение. Геометрическая сумма токов по модулю равна

.

Ток в нулевом проводе будет равен нулю, если ток , направ­ленный противоположно сумме , по модулю станет равным . При этом сопротивление фазы А

.

Пример 61. Определить ток в нулевом проводе схемы рис. 6.12, а, если в фазу А включить активное сопротивление 3,66 Ом, а индук­тивность и емкость фаз В и С поменять местами.

.

Решение. Векторная диаграмма изображена на рис, 6.13. Из нее следует, что

I₀ =34,6 +34,6 ==69,2 А.

Пример 62. В схеме рис. 6.14, a Z_AB = -19j; Z_BC = 19 Ом; Z_CA = 19 Ом. Э. д. с. каждой фазы генератора 220 В. Определить все токи и построить векторную диаграмму.

Рис. 6.14

Решение. Векторная диаграмма построена на рис. 6.14, б. Напряжения на фазах нагрузки в раз больше фазовых э. д. с. генера­тора и равны 220 = 380 В. Ток опережает напряжение на 90° и равен. Ток отстает от на 90° и также равен 20 А. Ток по модулю равен 20 А и совпадает по фазе с напряжением . Линейные токи найдем графически путем использования соотношений (6.4). По модулю .

Пример 63. Определить показания амперметра и вольтметра в схеме рис. 6.16. Построить топографическую диаграмму, совместив ее с век­торной диаграммой токов. Дано: .

Решение. Выберем положительные направления токов в соот­ветствии с рис. 6.16. По первому закону Кирхгофа, .

Рис 6.16

Примем э. д. с. направленной по оси +1. Составим уравнение по второму закону Кирхгофа для контура 0A0'B0:

.

После подстановки числовых значений получим

или

.

Для контура 0C0'B0

или

Совместное решение трех уравнений дает

.

Топографическая диаграмма, совмещенная с векторной диаграммой токов, изображена. На рис. 6.17.

Рис.6.17

Амперметр показывает 110. А, вольтметр – приблизительно 640 В. Последим, результат получен после подсчета по формуле:

.

Пример 65. В левой ветви схемы рис. 7.4, а имеется источник тока ik (t)=Ikmcos2t, в средней (второй) — источник э. д. с. e(t) = E0+Emsint. Индуктивность L4 магнитно связана с индуктив­ностью L3. Взаимная индуктивность между ними М. Определить мгновенное значение тока i3, и напряжения uba на зажимах L4. Дано:

Ikm=5А; =1000 рад/с; Е0=ЗВ; Еm=6 В; R1=3 Oм; L3=3 мГn;

М=1 мГn.

Решение. Положительные направления для токов выберем в соответствии с рис. 7.4, а.

По второму закону Кирхгофа,

но i4=0; поэтому uba=-M di3/dt

Воспользуемся принципом наложения и найдем составляющие тока i3 от каждого источника в отдельности.

Схема рис. 7.4, б служит для расчета токов от действия посто­янной составляющей э. д. с. Левая ветвь схемы разомкнута, так как в ней включен источник тока с бесконечным сопротивлением. Правая ветвь короткозамкнута, так как индуктивность для постоянного тока имеет нулевое сопротивление. При этом =E0/R1= 1 А.

*Строго говоря, активное сопротивление зависит от частоты вследствие явле­ния поверхностного эффекта. Явление поверхностного эффекта (см. ч. III учеб­ника) здесь не учитывается.

Первую гармонику тока находим, используя схему рис. 7.4, в:

=6/(3+3j)=1,41

Вторую гармонику тока находим в соответствии со схемой рис. 7.4, г:

Мгновенное значение тока i3 равно сумме мгновенных значений:

i3 = + + = 1 + 1,41 sin (t - 45°) + 2,23 sin (2t 4- 26°40') А.

Напряжение

иba=—М di3/dt=— 1,41 cos (t -45°) -4,46 cos (2t+26⁰40^`) В.

Пример 66. В схеме рис. 7.5 задана индуктивность L2. Полагая активное сопротивление индуктивной катушки равным нулю, найти, при каких значениях емкостей С1 и С2 входное сопротивление схемы для первой гармоники равняется нулю, а для девятой — бесконечности.

Решение. Запишем выражение для входного сопротивления схемы для первой гармоники и приравняем его нулю:

Приравняем бесконечности входное сопротивление для девятой гармоники:

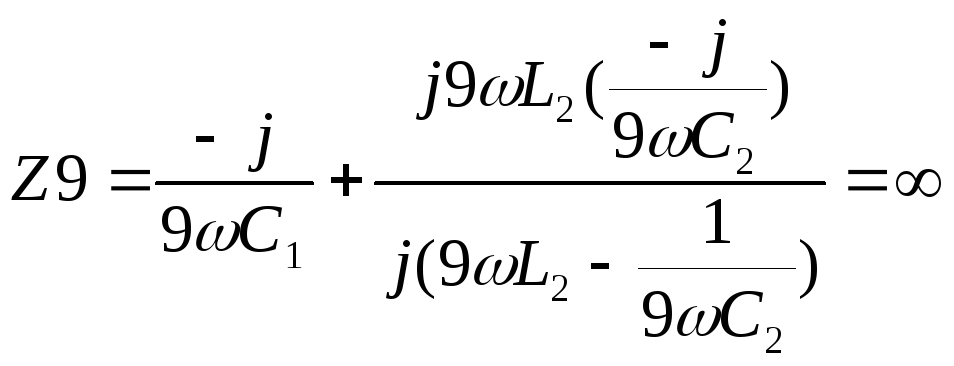
Совместное решение дает

Пример 67. На входе двухполюсника u= 100+80sin(t+30°) + 60 sin (3t+20°)+50 sin (5t+45°) В; i = 33,3+17,87 sin (t - 18) + 5,59 sin (5t+120°) А. Найти их действующие значения.

Решение.

В;

A.

Пример 68. Дана функция, не содержащая постоянной составляющей и четных гармоник и не изменяющая знака в течение каждого полупериода. Определить ее среднее по модулю значение.

Решение. Разложим заданную функцию в ряд Фурье:

i=I1m sin(t+1)+I3m sin (3t+3)+I5m sin (5t+5)+…

После интегрирования получим

Iср. по мод.=2/(I1m cos 1+1/3I3m cos 3+1/5I5m sin 5+… (7.13)

Пример 69. Найти Р и S, если

и = 25,9 sin (t – 11 40') + 6 sin (3t + 53°50') В;

i = 3 sin (t - 40°) + 0,9 sin (3t + 125°) A.

Решение.

U1=25,9/= 18,3 В; U3= 6/ =4,26 В;

I1 =2,13 А; I3=0,9 А;

1=—11⁰40'-(—40⁰)=28⁰20'; 3=-71 10`;

Р = 18,3 • 2,13 cos 28°20' + 4,26.0,9 cos (— 71°10^/) = 35,5 Вт;

U= =18,55 В;

/ = =2,31 А; S=UI= 18,55 • 2,31 = 42,8 ВА.

Пример 70. Заменить несинусоидальные ток и напряжение при­мера 69 эквивалентными синусоидальными и найти угол сдвига фаз э между ними.

Решение. Действующее значение синусоидального напряжения U=18,55 В; действующее значение синусоидального тока I=2,31 А;

cos э = 35,5/( 18,552,31) = 0,828;  э= 34°.

Пример 71. Мгновенное значение напряжения фазы А трехфазного генератора

U_A=127sin(t+10)+30sin(3t+20)+20sin(11t+15)В.

Определить мгновенное значение линейного напряжения uab при соединении генератора в звезду.

Рис 7.11

Рис. 7.12

Решение. В линейном напряжении третья гармоника отсутствует. Первые гармоники фаз A и В по фазе сдвинуты на 120°. Поэтому линейное напряжение U_AB первой гармоники в раз больше фазо­вого напряжения первой гармоники Uа и на 30° опережает его по фазе.

Одиннадцатая гармоника (обратная последовательность фаз) линей­ного напряжения отстает по фазе от одиннадцатой гармоники напря­жения фазы A на 30° и будет в раз больше ее:

u_AB=127sin(t+40⁰)+20sin(11t-15⁰)В.

Пример 72. э.д.с. фазы A в схеме рис. 7.11

e_A=170sin(t)+80cos(3t)+34cos(9t)

R=9Ом L=2Ом.

Определить показания всех приборов. Приборы электродинами­ческой системы.

Решение. Действующие значения э. д. с.

E1==121в E3=56.5в E9=24.2в

По линейным проводам течет первая гармоника тока

I1==13.2А.

Показание вольтметра V1 равно =136 В.

Показание вольтметра V2 равно I1R1=13,29= 118,5 В.

Показание вольтметра V3 равно 118.5=205 В.

Показание вольтметра V5 равно I1L=26,4 В.

Показание вольтметра V5 равно =62,3 В.

Пример 73. Э. д. с. каждой фазы генератора (рис. 7.12) изменяется по трапецеидальному закону: а_m=220 В; =Т/36; нагрузка рав­номерная;

R=6Ом; L == 0,5 Ом, 1/С=12 Ом.

Записать мгновенное значение тока по нулевому проводу, пре­небрегая гармониками тока выше седьмой.

Решение. С помощью табл. 7.1 записываем разложение трапе­цеидальной э. д. с.:

e_A=(sin10⁰sint+sin30⁰sin3t+

+sin50⁰sin5t+sin70⁰)sin7t

Следовательно,

e_A=274sint+89,3sin3t+49,5sin5t+30,9sin7t

По нулевому проводу протекает только третья гармоника тока

I₀₃=

где E₃==63,3в Z₀₃=1,5j Z_н3=6-4j

=2-1,33j I₀₃=31,8e^{—j4 40`}А

Мгновенное значение тока i₀₃=44,8sin(3t-4⁰40`)A.

Пример 75. Используя уравнение (8.8), составить характеристи­ческое уравнение для схемы рис. 8.4, а и найти его корни.

Решение.

или

Если дробь равна нулю, то равен нулю ее числитель. Следовательно,

(8.10)

Корни квадратного уравнения

В начале § 8.11 говорилось о том, что решение для свободного тока берется в виде Ае^pt. Если характеристическое уравнение имеет не один корень, а несколько, например n, то для каждого свобод­ного тока нужно взять

Пример 76. Найти корни характеристического уравнения схемы рис. 8.4, а при трех значениях С: 1) С=1 мкФ, 2) С =10 мкФ, 3) С ==100 мкФ, R₂=100 Ом; L₁=l Гн.

Решение. При С = 1 мкФ

При

При

Пример 77. Для схемы рис. 8.4, а входное сопротивление относительно зажи­мов аb при переменном токе

Заменим в нем j'o на р и приравняем его нулю:

Отсюда

или

(8.10`)

Уравнение (8.10') совпадает с уравнением (8.10), составленным иным путем. Уравнение (8.10') получено путем использования выражения для входного сопротивления первой ветви схемы рис. 8.4, а относительно зажимов аb. Точно такое же уравнение можно получить, если записать выражение для входного со­противления любой другой ветви.

Пример 78. Убедиться в том, что для схемы рис. 8.5 характери­стическое уравнение имеет не четвертую, а третью степень.

Решение. Составляем выражение для входного сопротивления:

Отсюда

Следовательно, характеристическое уравнение имеет третью степень.

Рис. 8.5

Рис. 8.6

Рис. 8.16

.

Пример 79. Выясьить, можно ли ожидать возникновгния электрической искры (дуги) при размыкании ключа в схеме рис 8.16

Решение До размыкания ключа в цепи был остановившийся режим:

Допустим, что при размыкании ключа искра не возникает. При этом ток почти мгновенно спадает до нуля, а должен будет равняться . Но каждый из токов () по первому закону коммутации не может измениться скачком.

Следовательно, между достаточно медленно расходящимися контактами ключа в схеме рис 8 16 при определенных условиях можно ожидать возникновения электрической искры (дуги). Расчет переходного процесса в схеме рис. 8.16 см. в § 8.28.

Пример 80. К зажимам индуктивной катушки R=100 Ом, L=10 Гн под­ключен вольтметр (рис. 8.17). Сопротивление вольтметра R_V=3000 Ом, E==100 В. Приближенно найти напряжение на зажимах вольтметра при t=0, если допу­стить, что размыкание ключа произойдет мгновенно и искры не возникнет.

Решение. До размыкания ключа через L проходит ток . В индуктивности была запасена магнитная энергия Если допустить, что размыкание ключа произошло мгновенно и искры не возникло, и учесть, что ток через индуктивность должен оставаться равным 1 А, то по замкнутому контуру, составленному вольтметром и катушкой, за счет запаса энергии магнитного поля индуктивности в первое мгновение будет проходить ток в 1 А. При этом на вольтметре возникнет пик напряжения порядка 3000 В. Прохождение большого импульса тока через вольтметр может вызвать перегорание катушки прибора и выход его из строя.

При размыкании ключа с конечной скоростью между его расходящимися контактами (рис. 8.17) возникнет электрическая искра (дуга). Это приведет к тому, что увеличение напряжения на вольтметре бу­дет меньше, чем в только что рассмотренном идеализированном случае, когда ключ размы­кался мгновенно без искры (дуги) ¹.

Чтобы не «сжечь» вольтметр в цепи рис. 8.17, сначала надо отключить вольтметр, а за­тем разомкнуть ключ.

Рис. 8.17

Перенапряжения проявляются тем сильнее, чем больше индуктивности в цепях. Особенно опасны они в цепях постоянного тока, содер­жащих индуктивности порядка единиц и десят­ков генри. В таких цепях при отключениях

соблюдают специальные меры предосторожности (отключение ключа после введе­ния дополнительных активных сопротивлении в цепь).

Пример 81. В схеме рис. 8.18 до замыкания ключа был установившийся режим:

Требуется: 1) найти полные, принужденные и свободные составляю­щие токов при t = 0₊, а также начальное значение производной от свободного напряжения на емкости; 2) определить токи и напряжение в функции времени.

Решение первой части задачи.

До коммутации

и .

Напряжение на емкости равнялось напряжению на сопротивле­нии R₃:

Найдем принужденные значения токов и напряжений после ком­мутации:

По второму закону Кирхгофа составим уравнение для контура, образованного первой и второй ветвями при t=0₊:

Поэтому

Из уравнения

получим

По первому закону Кирхгофа,

Следовательно,

Свободные составляющие тока и напряжения определим как раз­ности между полными и принужденными величинами.

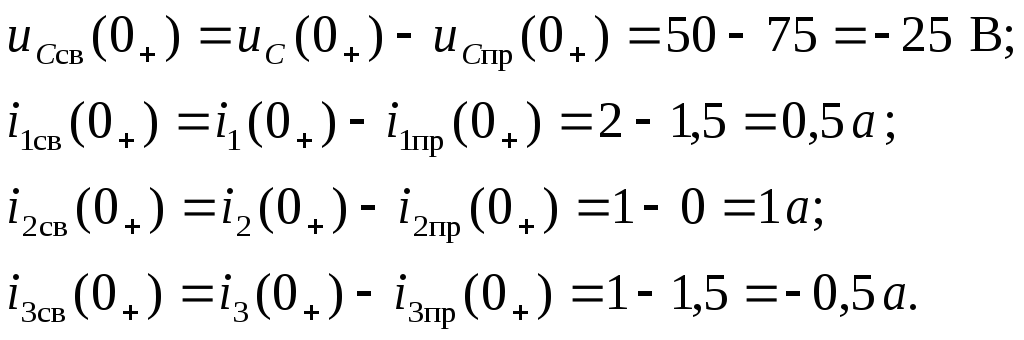
Так как свободный ток через емкость,

то

В рассматриваемом примере

Решение второй части задачи.

Характеристическое уравнение для послекоммутационной схемы имеет один корень

Каждый ток равен сумме принуж­денной составляющей и свободной состав­ляющей Ае^pt, где А равно значению сво­бодной составляющей при t=0₊ (рис. 8.19):

Рис 8.19

Рис. 8.20

Пример 82. В схеме рис. 8 20 до замыкания ключа был устано­вившийся режим: R₁=R₂==2 Oм, L==3 Oм, e(t)== 127 sin (t— 50°) В, =314 с ^–1.