КР_студентам_cбросить / Пособие_MathCAD / Лаб_3_Операторы Mathcad

40

3. Операторы MathCAD и их использование

Операторы используются в математической области и предназначены для выполнения различных операций над операндами. Они могут вводиться с клавиатуры, кнопками палитры инструментов, а также командами меню.

В среде Mathcad рассматриваются основные операторы:

- арифметические;

- векторов и матриц;

- вычислений;

- Булевы.

Рассмотрим их подробней.

Арифметические операторы

Арифметические операторы MathCAD реализуют обычные операции математики над операндами. В таблице 3.1 приведена панель арифметических операторов и их горячие клавиши для вызова их с клавиатуры.

Таблица 3.1.

Арифметические операторы MathCAD.

Операторы:		Горячие клавиши:
Панель Арифметика:	встроенные функции
	факториал	!
	мнимая единица	1i
	модуль переменной	|
	квадратный корень	\
	корень n-ой степени	[Ctrl]\
	функция ex	e^x
	pi (π)	p[Ctrl]g или [Ctrl][Shift]p
	смешанное число (целое с дробной частью)	[Ctrl][Shift]+
	сложение (+)	+
	вычитание (-)	-
	умножение (x)	*
	деление (/) запись дробью	/
	деление () запись в строку	[Ctrl]/
	присваивание (:=)	:
	Вычисление (=)	=

Приведем пример использования арифметических операторов:

Операторы векторов и матриц

Операторы векторов и матриц предназначены для выполнения разнообразных вычислений с векторами и матрицами. Одни из них доступны из панели Matrix, другие можно вызвать с помощью горячих “клавиш”, таблица 3.2.

Таблица 3.2.

Операторы векторов и матриц.

Операторы:		Горячие клавиши:
Панель Matrix:	создать матрицу	[Ctrl]M
	создать индекс	[
	получить обратную матрицу	^−1
	определитель матрицы и модуль	|
	векторизация	[Ctrl]−
	выделить из матрицы столбец	[Ctrl]6
	транспонирование	[Ctrl]1
	ранжирование переменной	;
	скалярное произведение матриц	*
	векторное произведение матриц	[Ctrl]8
	сумма элементов вектора	[Ctrl]4
	преобразовать матрицу в изображение	[Ctrl]T
На панели отсутствуют:	сложение матриц	+
	вычитание матриц	−
	умножение матриц	*
	возведение матрицы в степень	^
	деление матриц	/

Приведем несколько примеров использования операторов матриц:

Приведем пример использования векторизации. Пусть дано квадратное уравнение

где а, b, c – вектора из четырех аргументов каждый. Найти корни уравнения. Пусть

Приведем примеры некоторых операций с векторами.

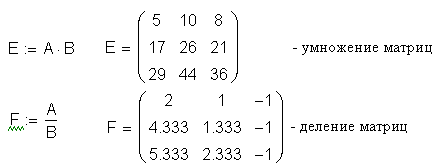
Операторы вычислений

Операторы вычислений предназначены для выполнения разнообразных вычислений. Они могут вводиться с клавиатуры или с помощью кнопок палитры, см. таблица 2.3. С их помощью можно выполнять операции дифференцирования, интегрирования, находить суммы и произведения рядов и т.д.

Таблица 2.3.

Операторы вычислений

	Оператор:	Горячие клавиши:
	Производная	?
	n-ая производная	[Ctrl]?
	бесконечность	[Ctrl][Shift]Z
	определенный интеграл	&
	неопределенный интеграл	[Ctrl]I
	суммирование	[Ctrl]$
	суммирование с ранжированной переменной	$
	произведение	[Ctrl]#
	произведение с ранжированной переменной	#
	двухсторонний предел	[Ctrl]L
	правосторонний предел	[Ctrl][Shift]A
	левосторонний предел	[Ctrl][Shift]B

Приведем несколько примеров использования операторов вычислений:

Оператор «производная» предназначен для нахождения численного значения производной функции в заданной точке. Производная вычисляется с точностью 7-8 значащих цифр:

Оператор «n-ая производная» предназначен для нахождения численного значения производной высокого порядка функции в заданной точке. Точность алгоритма уменьшается на одну значащую цифру при увеличении порядка производной на одну единицу:

Рис. 3.1. Функция и ее первая производная

Оператор «интегрирование» предназначен для численного интегрирования функции на некотором интервале [а,b]. Точность интегрирования зависит от вида функции (гладкая, наличие точек разрыва, асимптот и т.д.) и устанавливается системной переменной TOL. При изменении точности необходимо соблюдать компромисс между точностью и временем вычисления.

Рис.2.2. Функция и ее интеграл

Суммирование выражения Х по i возвращает сумму ( ∑ ) при X_i по m ≤ i ≤ n, т.е.

∑ = X_m + X_m+1 + X_m+2 + … + X_n

где i, m, n – целые. Выражение X_i может быть любым. Если Х имеет несколько слагаемых, то их нужно взять в круглые скобки. Переменная i определена только внутри оператора суммирования. Она может быть дискретным аргументом.

Аналогично сумме ( ∑ ) можно вычислить произведения ( ∏ ) выражений X_i.

MathCAD имеет три шаблона, используемые для вычисления пределов (только символически). Например,

Булевы операторы

Булевы операторы используются в вычисляемых, условных или аналитических выражениях и возвращают 0 или 1. Они вызываются кнопкой на математической палитре или с помощью главного меню View > Toolbars > Boolean (см. таблицу 3.4).

Приведем некоторые примеры использования булевых операторов:

Таблица 3.4.

Булевы операторы

	Операторы:	Горячие клавиши:
	Равно ()	[Ctrl] =
	Меньше чем ()	<
	Больше чем ()	>
	Меньше чем или равно ()	[Ctrl] 9
	Больше чем или равно ()	[Ctrl] 0
	Не равно ()	[Ctrl] 3
	Булево отрицание NOT ()	[Ctrl][Shift] 1
	Булево AND ()	[Ctrl][Shift] 7
	Булево OR ()	[Ctrl][Shift] 6
	Булево XOR ()	[Ctrl][Shift] 5

Лабораторная работа 3

Цель работы:

- изучить арифметические операторы, операторы векторов и матриц, операторы вычислений и булевы операторы;

- использовать операторы MathCAD при создании документов.

Задание 1. Привести примеры использования арифметических операторов. Создать сложное выражение, сформированное с помощью большинства кнопок панели «Арифметика» (см. таблицу 3.1).

Задание 2. Создать матрицу, инициализировать ее, напечатать некоторые ее элементы, получить транспонированную и обратную матрицы, найти ее определитель, максимальный и минимальный элементы, получить сумму, разность, скалярное и векторное произведение матриц, выполнить операции векторизации.

Задание 3. Выполнить операции дифференцирования и интегрирования функций, заданных в лабораторной работе 2 (таблица 2.1), построить графики функций и их первых и вторых производных. Построить интегральные функции. Привести примеры использования операторов сумм и произведений. Привести примеры использования шаблонов пределов функций.

Задание 4. Привести примеры использования всех булевых операторов.