1. Матричные уравнения.

Матричные уравнения простейшего вида с неизвестной матрицей Х записываются следующим образом АХ=В, ХА=В, АХС=В.

В этих уравнениях А, В, С, Х – матрицы таких размеров, что все используемые операции возможны, и с обеих сторон от знаков равенства находятся матрицы одинаковых размеров.

Если в этих уравнениях матрицы А, В, С – невырожденные, то решения этих уравнений можно записать следующим образом:

1. АХ=В  А^-1АХ=А^-1В  ЕХ=А^-1В  Х=А^-1В.

2. ХА=В  ХАА^-1=ВА^-1  ХЕ=ВА^-1  Х=ВА^-1

3. АХС=В  А^-1АХСС^-1=А^-1ХС^-1  ЕХЕ=А^-1ХС^-1  Х=А^-1ХС^-1

Пример 1. Решить уравнение АХ=Н

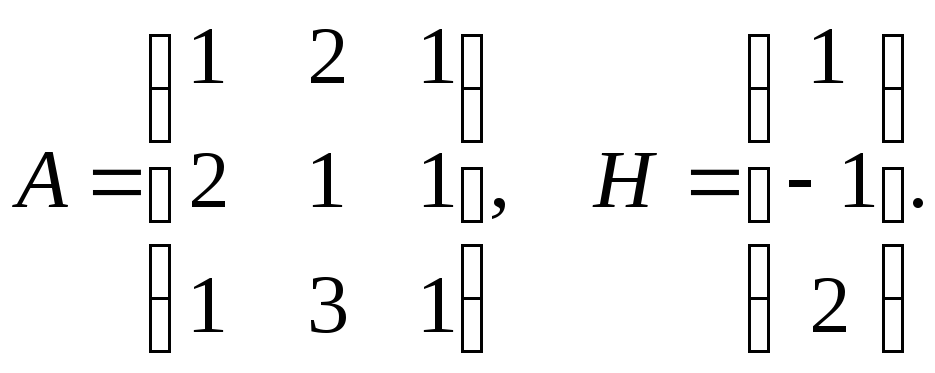
Решение Х=А^-1Н

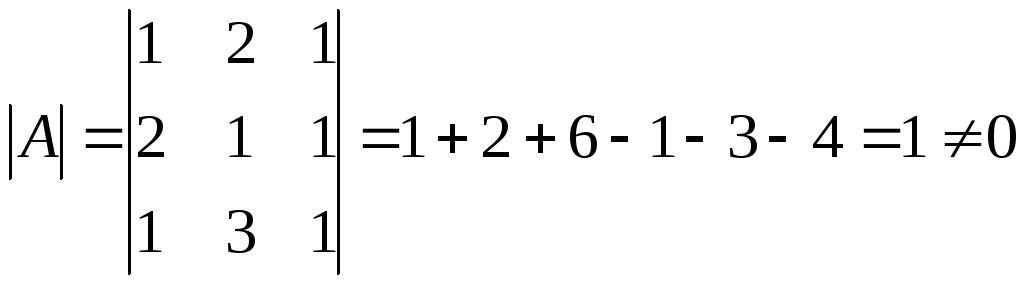. Следовательно матрица невырожденная.

Найдем обратную матрицу. Составим алгебраические дополнения элементов матрицы А.

Получаем .

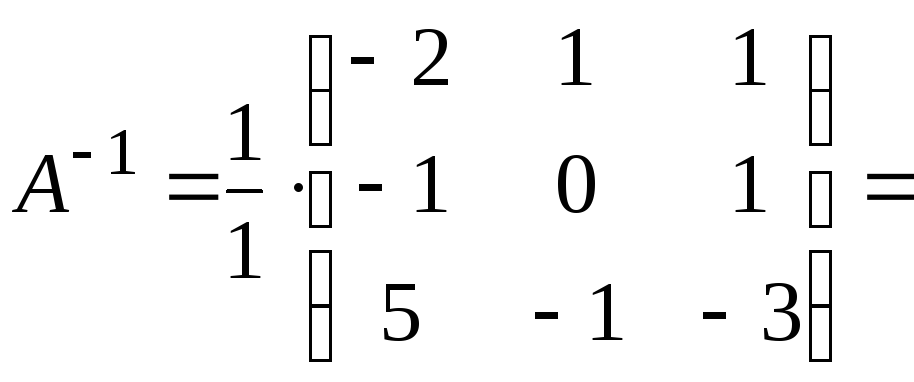
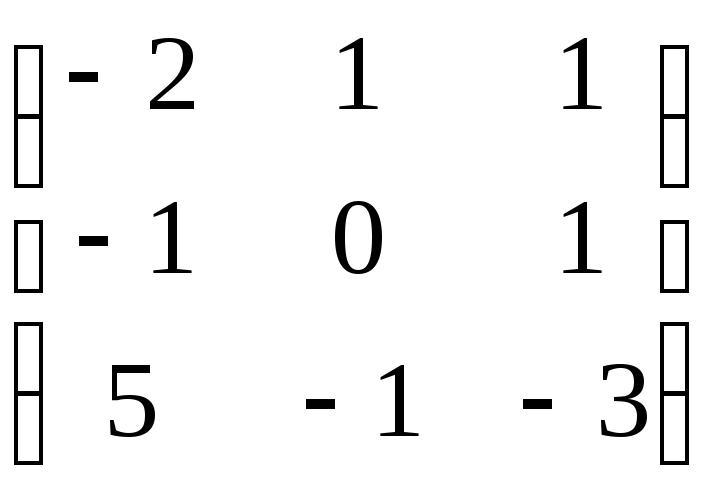Следовательно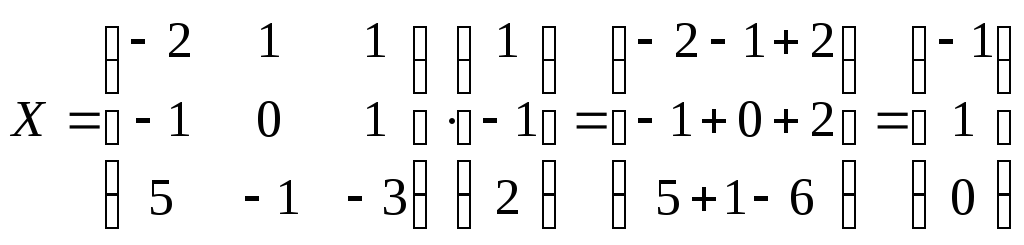

Теория матриц и определителей произвольного порядка строится аналогично изложенной теории матриц и определителей третьего порядка.

2. Системы линейных неоднородных уравнений

Пусть задана система m линейных уравнений с n неизвестными:

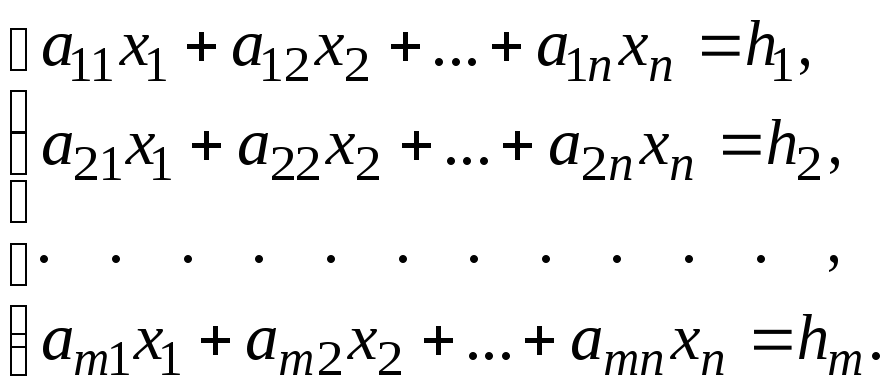(1)

Если , то система (1) называетсяоднородной. Если же хотя бы одно из этих чисел отлично от нуля, то система неоднородная.

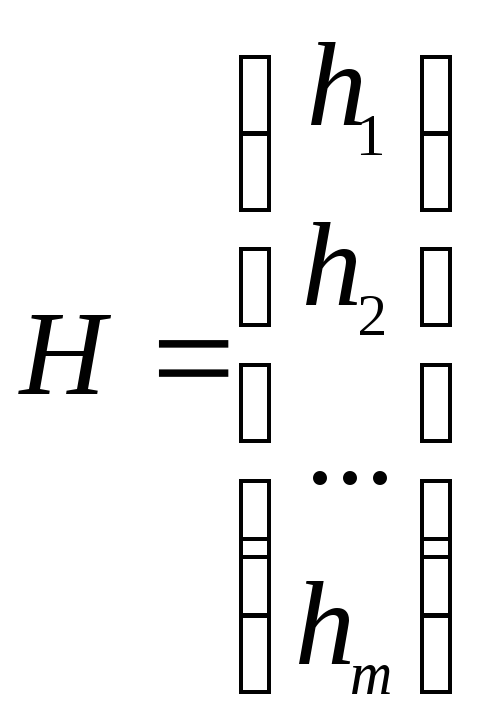Запишем систему вида (1) в матричном виде, обозначив матрицу коэффициентов при неизвестных , матрицу столбец свободных членов, матрицу столбец неизвестных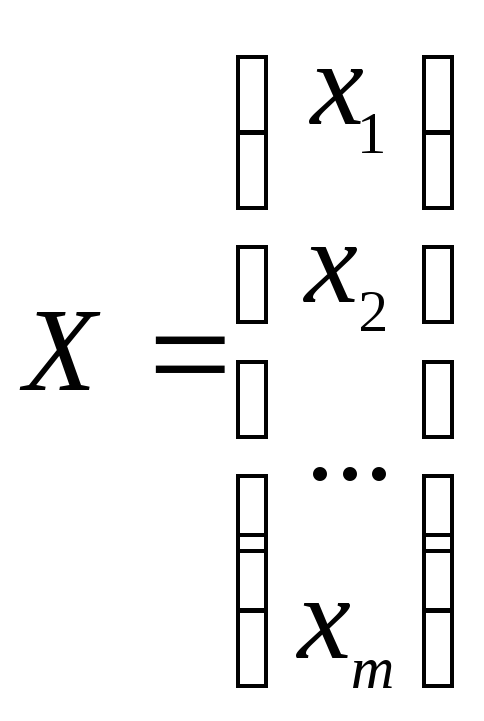. Умножая матрицы АХ, получаем новую матрицу, элементами которой являются левые части уравнений системы (1). На основании равенства матриц систему (1) можно записать систему (1) в виде АХ=В.

Определение 1. Решением системы линейных уравнений вида (1), называется такая совокупность n чисел (k₁, k₂, …, k_n), при подстановке которых каждое уравнение обращается в тождество.

Определение 2. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Определение 3. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Вопрос о разрешимости системы уравнений в общем виде рассматривается в следующей теореме.

Теорема Кронекера – Капели:

Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

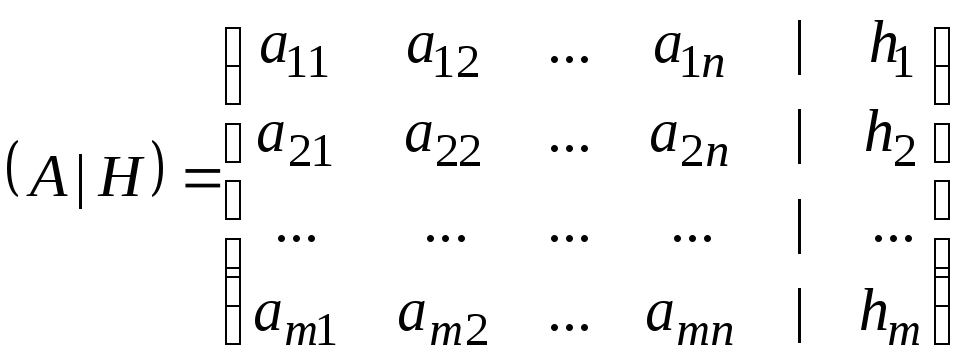- расширенная матрица.

Для определения рангов обеих матриц достаточно привести расширенную матрицу к ступенчатому виду с помощью элементарных преобразований строк и перестановки столбцов (кроме последнего).

Для совместных систем линейных уравнений верны следующие утверждения:

1. Если ранг матрицы совместной системы равен числу переменных, т.е. r(A) = n, то система уравнений (1) имеет единственное решение.

2. Если ранг матрицы совместной системы меньше числа переменных, т.е. r(A) < n, то система (1) неопределенная и имеет бесконечное множество решений.

Схема исследования системы m уравнений с n неизвестными

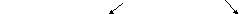
Система совместная, Система несовместная

если r(A) = r(B) = r. Если r(A)  r(B).

Ответ: нет решений.

Система определена, Система неопределенна,

если r = n. Если r < n.

Ответ: единственное решение. Ответ: бесконечное множество решений.

Пример 2. Дана система линейных уравнений 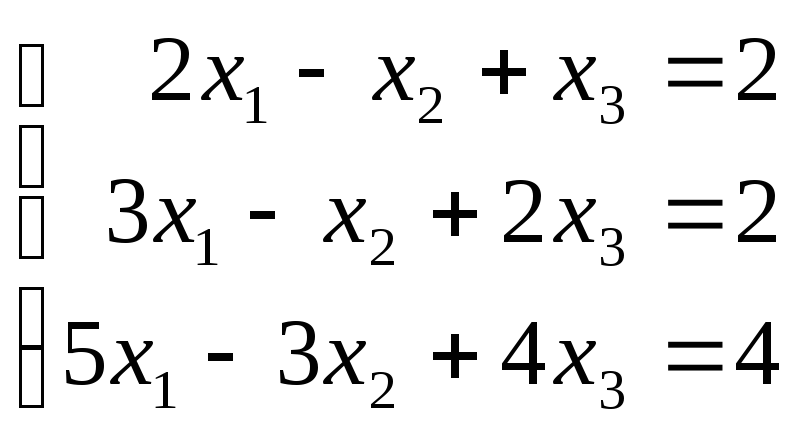. Доказать ее совместность.

Доказательство: Запишем расширенную матрицу системы

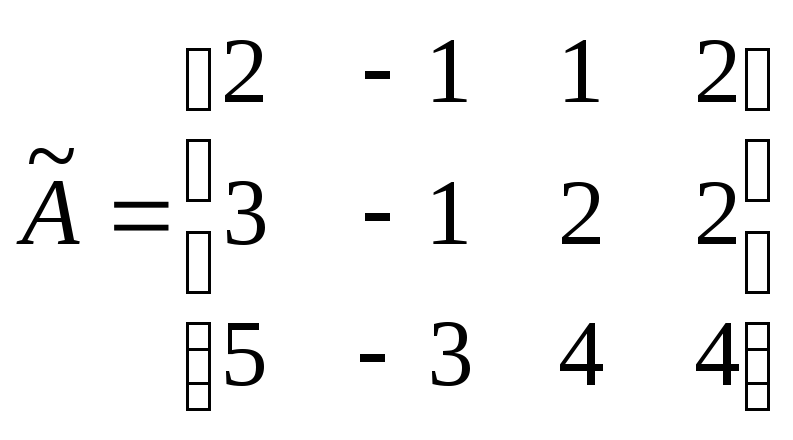
и найдем ее ранг. Элемент матрицы , стоящий в левом верхнем углу,отличен от нуля, следовательносреди миноров второго порядка, окаймляющих (включающих в себя) этот элемент, также есть отличные от нуля, например,

, т.е. .

Из миноров третьего порядка, окаймляющих , возьмем минор

:

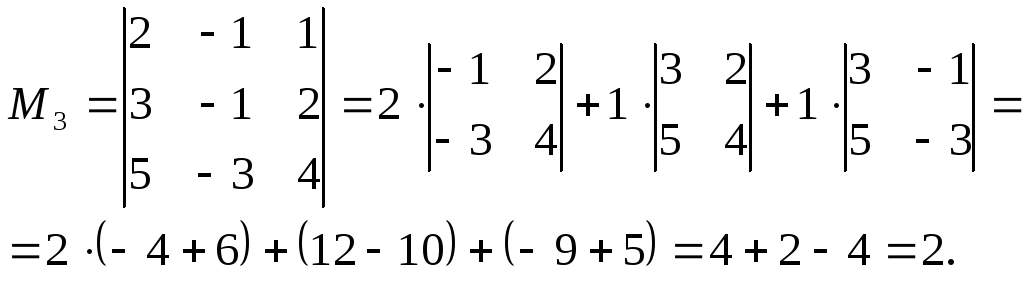
Т.к. то, а т.к. у матрицыминоров 4-го порядка не существует, то. Так как , то и . Таким образом, , и совместность доказана.

Пример 3. Исследовать систему линейных уравнений

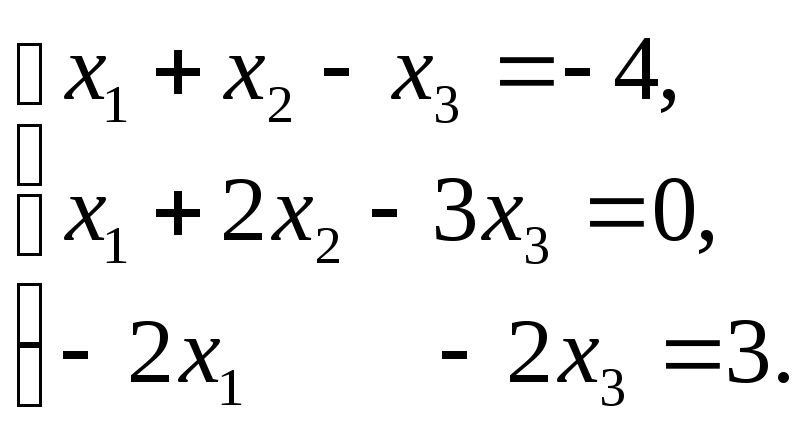
Решение: 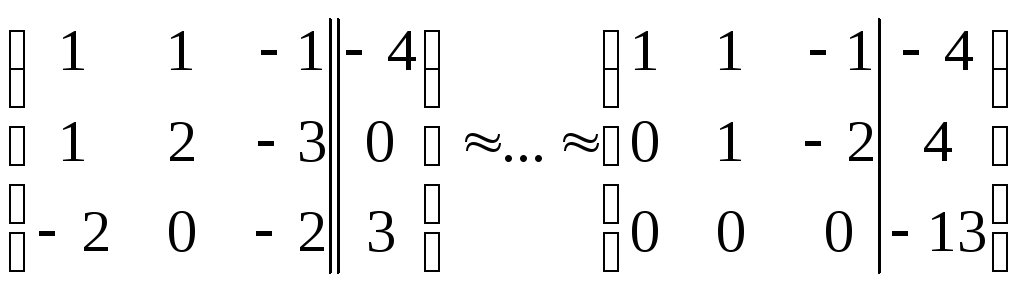, т.к., то система несовместна (не имеет решений). В самом деле, последней строке полученной расширенной матрицы соответствует уравнение, не имеющее решений.

Пример 4. Определить совместность системы уравнений:

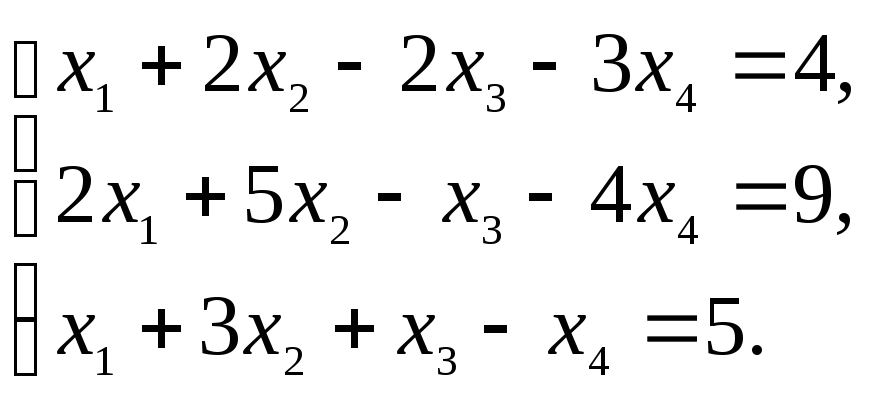
Решение:

Лекция 6. Решение систем линейных уравнений с помощью обратной матрицы.