35

Лекция 1. Матрицы. Действия с матрицами.

1.1 Понятие матрицы.

Определение 1. Матрицей А размера m  n называется прямоугольная таблица из m строк и n столбцов, состоящая из чисел или иных математических выражений (называемых элементами матрицы),i = 1,2,3,…,m, j = 1,2,3,…,n.

, или

Определение 2. Две матрицы иодного размера называютсяравными, если они совпадают поэлементно, т.е. =,i = 1,2,3,…,m, j = 1,2,3,…,n.

С помощью матриц легко записывать некоторые экономические зависимости, например таблицы распределения ресурсов по некоторым отраслям экономики.

Определение 3. Если число строк матрицы совпадает с числом ее столбцов, т.е. m = n, то матрица называется квадратной порядка n, а в противном случае прямоугольной.

Определение 4. Переход от матрицы А к матрице А^т , в которой строки и столбцы поменялись местами с сохранением порядка, называется транспонированием матрицы.

Виды матриц: квадратная (размера 33) - ,

прямоугольная (размера 25) - ,

диагональная - , единичная -, нулевая -,

матрица-строка - , матрица-столбец -.

Определение 5. Элементы квадратной матрицы порядка n с одинаковыми индексами называются элементами главной диагонали, т.е. это элементы: .

Определение 6. Элементы квадратной матрицы порядка n называются элементами побочной диагонали, если сумма их индексов равна n + 1, т.е. это элементы: .

1.2. Операции над матрицами.

1⁰. Суммой двух матриц иодинакового размера называется матрица С = (с_ij), элементы которой определяются равенством с_ij = a_ij + b_ij, (i = 1,2,3,…,m, j = 1,2,3,…,n).

Свойства операции сложения матриц.

Для любых матриц А,В,С одного размера выполняются равенства:

1) А + В = В + А (коммутативность),

2) (А + В) + С = А + (В + С) = А + В + С ( ассоциативность).

2⁰. Произведением матрицы на число  называется матрица того же размера, что и матрица А, причемb_ij = (i = 1,2,3,…,m, j = 1,2,3,…,n).

Свойства операции умножения матрицы на число.

1. (А) = ()А (ассоциативность умножения);

2. (А+В) = А+В (дистрибутивность умножения относительно сложения матриц);

3. (+)А = А+А (дистрибутивность умножения относительно сложения чисел).

Определение 7. Линейной комбинацией матриц иодинакового размера называется выражение видаА+В, где  и  - произвольные числа.

3⁰_. Произведением АВ матриц А и В соответственно размеров mn и nk называется матрица С размера mk, такая, что элемент с_ij равен сумме произведений элементов i-той строки матрицы А и j-того столбца матрицы В, т.е. с_ij = a_i1b_1j+a_i2b_2j+…+a_ikb_kj.

Произведение АВ существует, только в том случае, если число столбцов матрицы А совпадает с числом строк матрицы В.

Свойства операции умножения матриц:

1. (АВ)С = А(ВС) (ассоциативность);

2. (А+В)С = АС+ВС (дистрибутивность относительно сложения матриц);

3. А(В+С) = АВ+АС (дистрибутивность относительно сложения матриц);

4. АВ  ВА ( не коммутативность).

Определение 8. Матрицы А и В, для которых АВ = ВА, называются коммутирующими или перестановочными.

Умножение квадратной матрицы любого порядка на соответствующую единичную матрицу не меняет матрицу.

Определение 9. Элементарными преобразованиями матриц называются следующие операции:

1. Перемена местами двух строк (столбцов).

2. Умножение каждого элемента строки (столбца) на число, отличное от нуля.

3. Прибавление к элементам одной строки (столбца) соответствующих элементов другой строки (столбца).

Определение 10. Матрица В, полученная из матрицы А с помощью элементарных преобразований называется эквивалентной (обозначается ВА).

Пример 1.1. Найти линейную комбинацию матриц 2А–3В, если

, .

Решение:

, ,

.

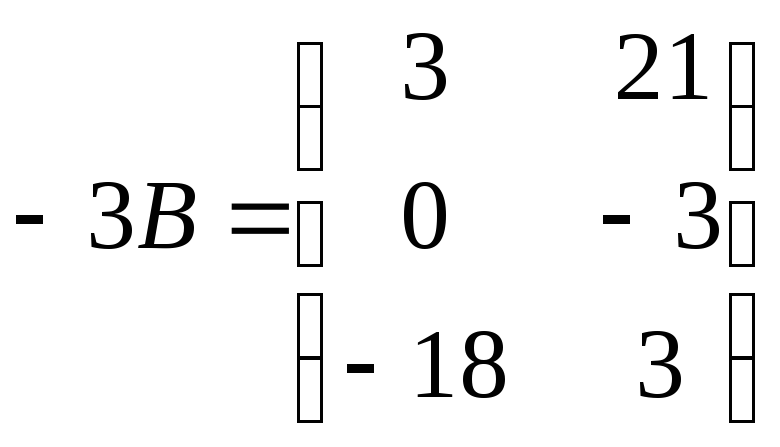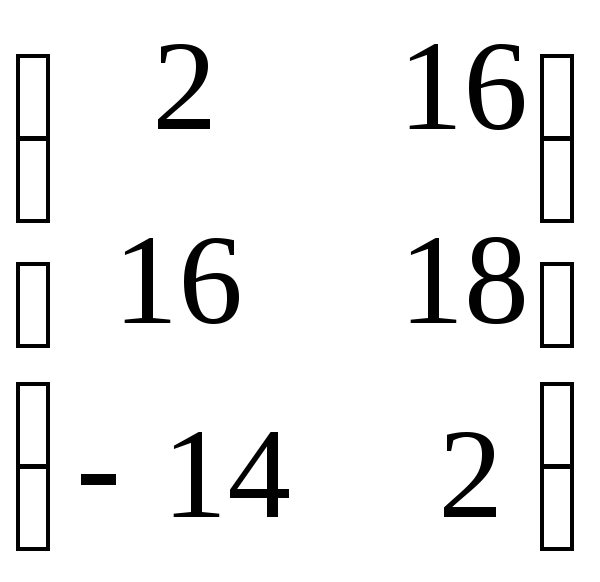
Пример 1.2. Найти произведение матриц , если

.

Решение: т.к количество столбцов первой матрицы совпадает с количеством строк второй матрицы, то произведение матриц существует. В результате получаем новую матрицу , где

В результате получим .

Лекция 2. Определители. Вычисление определителей второго, третьего порядка. Свойства определителей n-го порядка.