
Контрольная работа №3 и 4(математика)
.pdfМинистерство образования и науки РФ
Северный Арктический федеральный университет им. М.В.Ломоносова
Кафедра математики
Теоретические вопросы по курсу математики
для студентов заочной формы обучения
специальности 270100.62 «Промышленное и гражданское строительство»
2семестр
1.Производная функции. Ее геометрический и физический смысл. Уравнение касательной и нормали к кривой. Свойства операции дифференцирования.
Производные элементарных функций.
2.Производная сложной, обратной и параметрически заданной функций.
Логарифмическое дифференцирование. Связь между непрерывностью и дифференцируемостью.
3.Дифференциал функции, его геометрический смысл, свойства. Применение дифференциала к приближенным вычислениям.
4.Основные теоремы дифференциального исчисления: теоремы Ролля, Лагранжа,
Коши. Раскрытие неопределенностей по правилу Лопиталя.
5.Производные и дифференциалы высших порядков.
6.Исследование функций при помощи производных: монотонность, экстремум функции, выпуклость и точки перегиба. Асимптоты графика функции. Общая схема исследования функции и построения её графика.
7.Первообразная и неопределённый интеграл. Замена переменной в неопределённом интеграле; интегрирование по частям.
8.Интегрирование простейших дробей четырех типов. Интегрирование дробно-
рациональных функций. Разложение рациональных дробей на простейшие.
9.Интегрирование тригонометрических функций.
10.Интегрирование некоторых иррациональных выражений. Тригонометрические подстановки.
11.Определенный интеграл: определение, свойства. Геометрический смысл.
Условия интегрируемости функций.
1
12.Интеграл с переменным верхним пределом и его дифференцирование.
Формула Ньютона-Лейбница.
13.Геометрические приложения определённых интегралов: вычисление площади плоской фигуры, длины дуги, объема тела вращения и площади поверхности вращения.
14.Несобственные интегралы. Определения, свойства. Признаки сходимости.
15.Числовой ряд и его сумма. Необходимое условие сходимости ряда.
16.Достаточные признаки сходимости знакоположительных числовых рядов: два признака сравнения, признак Даламбера, радикальный и интегральный признаки Коши.
17.Знакочередующиеся ряды. Теорема Лейбница. Знакопеременные ряды.
Абсолютная и условная сходимость знакопеременных числовых рядов.
18.Степенные ряды. Радиус и интервал сходимости степенного ряда. Теорема Абеля. Дифференцирование и интегрирование степенного ряда.
19.Ряды Тейлора. Достаточные условия разложения функции в ряд Тейлора.
Разложение элементарных функций в ряд Тейлора. Приложения степенных рядов.
|
Составила: Л.А. Баданина |
|
Утверждаю: |
|
|
Зав. кафедрой математики |
________________________ |
В.Н. Попов |
|
|
18.01.2012. |
2

Контрольные работы № 3, 4.
Дифференциальное и интегральное исчисление. Ряды.
Задание 1. Вычислить первую производную yx .
1. |
1 |
|
|
|
|
|
||
а) y e |
ln 3 5x |
tg3 2x; |
||||||
б) y |
|
arcsin5x |
|
3 |
|
; |
||
|
|
|
5 |
|||||
|
|
|
|
|||||
|
|
|
1 25x2 |
|||||
2.а) y 3x 3x2 5arctg2 5x;
б) y 
 1 2x tg2;
1 2x tg2;
1 2x
3.а) y 3 51 3x arcsin2 3x;
б) y |
|
cos4x |
|
34 |
|
; |
|
|
5 |
||||
|
|
|
||||
|
|
6x2 3 |
||||
4.а) y 10
 3x 5 arcsin x2 ;
3x 5 arcsin x2 ;
б) y arctg3x sin3;
9x2 1
5.а) y e 3x 2arcctg
 7x 3 ;
7x 3 ;
б) y |
1 |
|
|
3 cos5x |
; |
||
|
|
|
x2 |
3x |
|||
|
|
||||||
|
|
|
|
|
|||
6.а) y 4sin2 3x 5 3
 3 5x ;
3 5x ;
б) y x2 5x 
 5 ; ln3x
5 ; ln3x
в)
г)
в)
г)
в)
г)
в)
г)
в)
г)
в)
г)
y 2x 5 2 3x ;
|
x |
cos5t |
. |
|
|
|
|
y t 2sin3t |
|
||
ln3x
y 3 2x ;
|
x 2 |
t |
|
|||
|
|
. |
||||
|
|
1 |
t |
3 |
1 |
|
y |
|
|
|
|||
4 |
|
|
||||
|
|
|
|
|
|
|
ysin 3x 2x 3 ;
x 1 t2 ;
y t t3
y x3 4 tg 4x ;
x ln3t
y 6t t2 .
yxarcsin23x ;
x t 1
|
t t |
1. |
|
|
|||
y |
|
|
|
|
|
|
|
t
yarcsin3x 2x ;
x ctg 3 3t .
|
y 4t |
3

7.а) y lg cos3x sin3 3x;
б) y |
|
84 x |
|
3 |
|
; |
|
|
2 |
||||
|
|
|
||||
|
1 3x2 |
|||||
8.а) y 1 53
 x 10 ln3 7x;
x 10 ln3 7x;
б) y arcsin3x 3 5;
5; 
 1 9x2
1 9x2
9.а) y 102x 5 sin3 4x;
б) y 2 2
 x 2 3
x 2 3 4 ; arcco3x
4 ; arcco3x
10.а) y arcsin3 5x 3
 3 2x ;
3 2x ;
б) y 2sin2x 
 ;
; 
 2 3x
2 3x
в)
г)
в)
г)
в)
г)
в)
г)
y 3x 5 
 4 3x ;
4 3x ;
x ln 1 ty 2 5t2 .
y log3 7x x2 ;
|
3 |
t. |
x 3cos |
|
|
y 4sin3 |
t |
|
yln5x 6 4x ;
x 3t2 2t
y 5t2 2t.
y3x2 1 cos2 5x ;
x log |
3 |
t |
|
|
|
. |
|
|
y t2 |
|
|
Задание 2. Составить уравнения касательной и нормали к данной кривой в точке M0
(1; 1).
1. |
2exy ex ey . |
|
2. |
|
x3 y3 2xy2 . |
||||||||
3. |
3x2 y2 2xy 2. |
4. |
10x2 9y2 xy. |
||||||||||
5. |
3 x 2 2 y2 xy 1. |
6. |
|
xsin |
πy |
ysin |
πx |
2. |
|||||
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
2 |
|
||||
7. |
sin y x2 3xy2 |
3. |
8. |
|
x |
xy x y2 . |
|||||||
|
|
||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|||
9. |
|
y |
x 2xy2 . |
|
10. |
|
x4 6x2 y2 |
3y3 2 0. |
|||||
|
|
|
|
||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
4

Задание 3. Провести полное исследование функции, на основании полученных данных построить графики функции.
|
|
2x2 |
|
y cosx. |
1. |
а) |
y x2 4 ; |
б) |
2. |
а) |
y |
x |
|
|
; |
|||
x2 1 |
||||
3. |
а) |
y |
x2 |
3 |
; |
|
x 1 |
||||||
|
|
|
||||
x2
4.а) y x2 16 ;
5. |
а) |
y x |
4 |
; |
|
x2 |
|||||
|
|
|
|
6. |
а) |
|
|
x3 |
|
||||
y x2 1; |
|||||||||
|
|
||||||||
7. |
а) |
y |
|
x2 |
12 |
|
|||
|
x 4 ; |
||||||||
|
|
|
|
||||||
8. |
а) |
y |
x2 |
1 |
|||||
|
|
|
|
|
|||||
|
x . |
||||||||
|
|
|
|
|
|||||
x2
9.а) y x 3;
10. |
а) |
y |
x2 |
; |
|
9 x2 |
|||||
|
|
|
б)
б)
б)
б)
б)
б)
б)
б)
б)
y ln sinx cosx .
y 1 sinx cosx .
sinx cosx .
y 
 sinx.
sinx.
y ln cosx sinx .
y ln 
 2sinx .
2sinx .
y ln 
 2cosx .
2cosx .
y e 
 2cosx .
2cosx .
y 3 sinx.
sinx.
y ln 
 2sinx .
2sinx .
Задание 4. Найти неопределенные интегралы.
5

1. а) 16xdx ;
1 4x2
б) 2xln(3x 1)dx;
2. а) |
|
|
|
dx |
|
; |
||
|
2 |
|
|
|
||||
cos |
3x 1 2tgx |
|||||||
|
|
|
|
|
||||
б) |
xsin 2xdx; |
|
|
|||||
3. а) |
|
x3dx |
|
|
; |
|
|
|
|
||
4 x |
4 |
||||
|
|
|
|
|
б) x32x 1dx;
4. а) |
sin xdx |
|
; |
2 |
|
||
|
16 cos |
x |
|
б) (1 6x)sin3xdx;
5.а) sin xcos2 xdx;
б) ln(x2 4)dx;
6.а) xex2 dx;
б) 3x2 ln xdx;
в) |
|
4x3dx |
; |
|
|||
(x 1) |
2 |
(x 3) |
|
||||
|
|
|
|
|
|||
г) |
|
|
|
dx |
|
; |
|
3 sin x 2cosx |
|||||||
|
|
|
|||||
в) (2x3 3)dx ; x3 2x 12
dx
г) 2sin x cosx 1;
в) (2x3 1)dx ;
x2 4 x
dx
г) sin2 x 5cos2 x ;
в) |
|
|
|
6x3dx |
; |
|
|
|
|||
x |
3 |
|
|
|
|
||||||
|
|
|
|
2x 3 |
|
|
|
||||
г) |
|
|
|
|
|
|
4dx |
|
|
; |
|
|
4sin |
2 |
x 9cos |
2 |
|
||||||
|
|
|
|
|
x |
||||||
в) |
|
|
|
|
x |
3dx |
|
|
|
; |
|
x |
3 |
x |
2 |
|
|
|
|
||||
|
|
|
|
2x 2 |
|||||||
г) |
|
|
|
|
|
dx |
|
|
; |
||
sin |
2 |
x 3cos |
2 |
|
|||||||
|
|
|
|
x |
|||||||
в) |
|
(x3 |
8)dx |
; |
|
|
|||
x(x |
2 |
9) |
|
|
|||||
|
|
|
|
|
|
||||
г) |
|
|
|
|
dx |
|
|
; |
|
sin x cosx 1 |
|||||||||
|
|
|
|||||||
д) |
|
|
dx |
|
|
; |
|
|
4 |
|
|
||
|
|
|||||
|
|
x |
x |
|||
е) 
 4 3x 5x2 dx.
4 3x 5x2 dx.
д) 15x
 2 xdx;
2 xdx;
е) |
|
dx |
|
|
|
. |
|
|
|
|
|
||
3 2x |
5x |
2 |
||||
|
|
|
|
|
д) |
|
|
|
dx |
|
|
; |
|
|
||
6 |
|
3 |
|
|
|||||||
|
|
||||||||||
|
|
|
|
x 2 |
x |
||||||
е) |
|
|
|
|
dx |
|
|
. |
|||
|
|
|
|
|
|
|
|
||||
3x |
2 |
|
|||||||||
|
|
|
|
5x 1 |
|||||||
д) |
x 1dx |
|
; |
|
|
|
|
||
|
|
|
||
|
3 |
x 1 |
||
е) 
 5x 3x2 dx .
5x 3x2 dx .
1 |
|
|
|
x |
|
|
|
|
|
|
|
д) |
|
|
|
|
|
|
dx; |
|
|
|
|
2 |
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
|||||||
0 |
|
|
x |
|
|
|
|||||
е) |
|
|
|
|
|
dx |
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
||
|
1 3x 4x |
2 |
|||||||||
|
|
|
|
|
|||||||
д) |
|
|
|
dx |
|
|
; |
|
3 |
|
|
|
|
|
|||
x |
2 |
2 |
||||||
|
||||||||
|
|
|
x |
|||||
е) 
 5x 8x2 dx.
5x 8x2 dx.
6

7. |
а) |
|
(1 2sin x)dx |
; |
||
|
cos |
2 |
x |
|||
|
|
|
|
|
||
б) (x 1)e 4xdx;
8. а) |
|
arctg2 2xdx |
; |
2 |
|||
|
|
1 4x |
|
б) |
(2x 4)cosxdx; |
||
9. а) |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
||
arcsin |
3 |
2x |
1 4x |
2 |
|
||
|
|
|
|
|
|||
б) |
xcos3xdx ; |
|
|
|
|||
10. |
|
exdx |
|
|
|
а) |
|
|
|
|
; |
|
|
|
|
||
9 e |
2x |
||||
|
|
|
|
|
|
б) (2x 1)e 3xdx;
в)
г)
в)
г)
;в)
г)
в)
г)
|
|
|
|
x3dx |
|
|
|
|
|
; |
|
|
|||
|
x |
3 |
2 |
|
|
|
|
|
|
|
|||||
|
|
|
2x |
|
1 |
|
|
||||||||
|
|
|
|
dx |
|
; |
|
|
|
|
|
|
|
|
|
cosx 3 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
(x3 12)dx |
|
; |
||||||||||
|
(x 2)(x 2) |
2 |
|||||||||||||
|
|
|
|
||||||||||||
|
|
|
sin xdx |
|
|
; |
|
|
|
|
|||||
(1 sin x) |
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
(9x3 18)dx ; |
|||||||||||||
|
|
x(x2 |
9) |
|
|
|
|||||||||
|
|
|
|
|
dx |
|
|
||||||||
5 4sin x 3cosx |
|||||||||||||||
|
|
|
|
x3dx |
|
|
|
; |
|
||||||
|
6x |
3 2 |
|
|
|
|
|||||||||
|
|
x |
|
7 |
|
|
|||||||||
|
|
|
|
dx |
|
|
|
|
; |
|
|
|
|||
sin xcos |
2 |
|
|
|
|
|
|||||||||
|
|
|
x |
|
|
||||||||||
д)
е)
д)
е)
д)
;е)
д)
е)
dx
1 
 2x 1 ;
2x 1 ;
dx

 x2 10x 29 .
x2 10x 29 .
1 3dxx 8 ;
dx

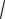 x2 6x 5 .
x2 6x 5 .
xdx
4 3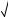 x ;
x ;

 3 5x 6x2 dx .
3 5x 6x2 dx .

 xdxx 3
xdxx 3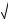 x2 ;
x2 ;
dx

 7x2 4x 13 .
7x2 4x 13 .
Задание 5. Вычислить площадь фигуры, ограниченной замкнутой кривой, заданной полярными координатами. Сделать чертеж.
1. |
cos4 . |
6. |
sin 4 . |
2. |
cos5 . |
7. |
sin5 . |
3. |
cos6 . |
8. |
sin6 . |
4. |
cos . |
9. |
sin . |
5. |
cos2 . |
10. |
sin2 . |
7

Задание 6. Вычислить длину
уравнениями.
1.x et cost sint ,
y et cost sint
0 t
4
2.x t2 2 sint 2tcost,
y 2 t2 cost 2tsint
0 t
3.x 2cos3 t,
y 2sin3 t
0 t
4
4.x 2 cost tsint ,
y 2 sint tcost
0 t
2
5.x 4 2cost cos2t ,
y 4 2sint sin 2t
0 t
дуги кривой, заданной параметрическими
6.x 2 t sint ,
y 21 cost
0 t
2
7.x 3 t sint ,
y 31 cost
t 2
8.x t2 1,
y t 1
1 t 1
9.x 2cost cos2t,
y 2sint sin 2t
0 t
2
10.x 4 t sint ,
y 41 cost
0 t
Задание 7. Вычислить объем тела, образованного вращением фигуры, заданной неравенствами, вокруг указанной оси. В вариантах 1-5 – оси Ох , в вариантах 6-10 -
оси Оу. Сделать чертеж.
1. |
y 1, |
|
|
y x2 2x 1. |
6. |
|
|
|
|
|
|
|
|
y 1. |
|||||||
|
|
y |
x 1, x 1, |
||||||||||||||||||
2. |
|
|
x, |
y 4, x 2. |
7. |
y2 2x 2, |
|
x 9. |
|
||||||||||||
|
y 4 |
|
|||||||||||||||||||
3. |
y x2 1, |
y 2. |
|
8. |
y 1, |
|
y x2 2x 1. |
||||||||||||||
4. |
x 2 |
|
|
|
|
x 0, |
y 4. |
9. |
x 2 |
|
|
|
x 2, y 0. |
||||||||
|
y 4, |
y 4, |
|||||||||||||||||||
5. |
y |
|
|
x 1, y |
1. |
10. |
y x2 |
4, |
y 4, |
x 2. |
|||||||||||
x 1, |
|||||||||||||||||||||
8

Задание 8. Вычислить несобственные интегралы или доказать их расходимость.
1. |
а) |
|
|
dx |
|
; |
б) |
2 |
|
dx |
. |
|
|
|
|
0 |
|
|
|||||||
|
|
2 x 1 x3 |
|
x 2 x 3 |
|
|||||||
2. |
а) |
cosx |
dx; |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x2 3 |
|
|
|
|
|
||||||||||||||
3. |
а) |
|
|
|
|
|
dx |
|
|
; |
|
|
|
|
|
||||||
e |
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
ln x |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. |
а) |
e x2 dx; |
|
|
|
|
|
||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
а) |
|
|
|
|
|
xdx |
|
|
|
|
; |
|||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x4 |
3x2 |
4 |
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
а) |
|
|
|
|
|
|
|
xdx |
|
|
|
; |
||||||||
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x2 6x 12 3 |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
ln x |
|
|
|
|
|
|
|||||||||
7. |
а) |
|
|
|
|
dx; |
|
|
|
|
|
||||||||||
|
x |
3 |
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
|
|
2x |
|
|
|
|
|
||||||||
|
а) |
|
|
|
|
|
|
|
xdx |
|
|
; |
|
|
|||||||
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x6 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2x 3 |
|
|
||||||||||||||
dx
9.а) 3 1 x2 ;
1 x2 ;
|
а) |
|
xdx |
|
; |
||
10. |
|
|
|
||||
|
|
|
|
||||
0 3 x8 3x4 4 |
|||||||
|
|
|
|
||||
|
1 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
|
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||
|
x 3 x 2 |
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
4 x |
2 |
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
|
|
|
|
|
. |
|
|
|
|
|
||||||||
x x 2 |
|||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
xdx |
|
|
|
|
|
|
|
|
|
|
||||
б) |
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
2 |
|
|
|
|
|
|
||||||||||
|
0 |
|
|
3x 4 |
|||||||||||||||
|
5 |
|
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||
|
x 5 |
2 |
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
1 x |
2 |
|
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
2 |
4 2x |
|||||||||||||||||
|
2 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||
|
x x 2 |
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задание 9. Исследовать на сходимость числовые ряды.
1. |
|
2 |
|
|
|
|
4 |
|
|
|
|
6 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
а) |
|
|
|
|
...; |
в) |
|
|
|
; |
|
|
|
|
|
|||||||||||||||||
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
3nlnn |
|
|
|
|
||||||||||||||||||
|
|
|
|
19 |
|
29 |
|
|
|
n 2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
2n |
3 |
|
|
|
n2 |
|
|
n |
|
|
2n |
|
|
|||||||||||||
|
б) |
|
|
; |
г) 1 |
|
|
3 |
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3n |
|||||||||||||||||||
|
|
n 0 |
3n 2 |
|
|
n 0 |
|
|
4n |
5 |
|
|
||||||||||||||||||||
2. |
|
2 |
|
|
|
4 |
|
|
|
|
6 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
а) |
|
|
|
|
...; |
в) |
|
|
|
; |
|
|
|
|
||||||||||||||||||
|
3 |
|
27 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
3nln |
2 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
9 |
|
|
|
|
|
|
n 2 |
|
|
n |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
9n2 |
|
|
1 |
n |
|
|
|
|
||||||||||
|
б) |
1 |
|
|
|
; |
г) |
|
|
|
|
|
. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
n 1 |
|
|
|
n |
|
|
n2 33n |
|
|
|||||||||||||||||||||
9

3. |
а) |
1 |
|
|
4 |
|
|
|
7 |
|
...; |
||
|
3 |
|
9 |
|
27 |
||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
n 3 |
n |
||||||
|
б) |
|
|
|
|
|
|
|
|
; |
|||
|
|
|
|
3 |
8 |
||||||||
|
|
n 3 |
n |
|
|
||||||||
4.а) 3 7 11 ...;
|
|
2 |
|
|
|
8 |
|
|
|
|
32 |
|
|
|
|
|
|||
|
|
|
|
|
|
2n 2 n2 |
|
||||||||||||
|
б) |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
n 2 |
2n 3 |
|
|
|
|||||||||||||
5. |
а) |
3 |
|
|
|
5 |
|
|
|
7 |
|
|
9 |
|
...; |
||||
|
3 |
|
|
9 |
|
15 |
|
21 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
n 1 |
3n |
|
|||||||||||
|
б) |
|
|
|
|
|
|
|
|
|
; |
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
n 2 |
n |
|
|
1 |
|
|
|
||||||||||
6. |
а) |
5 |
|
|
7 |
|
|
|
9 |
|
|
11 |
...; |
||||||
|
1 |
|
6 |
|
|
13 |
|
22 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
2n |
|
||||||
|
б) |
|
|
|
|
|
|
|
|
|
|
; |
|||||||
|
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
n 2 |
3n |
|
|
1 |
|
|
|
||||||||||
7.а) 1 5 9 ...;
|
|
2 |
|
|
|
4 |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n |
|
|||||||||
|
б) |
|
|
|
|
|
|
|
|
; |
||||||
|
|
|
|
|
|
|
||||||||||
|
|
n 1 |
2n 1 |
|
||||||||||||
8. |
а) |
1 |
|
|
3 |
|
|
5 |
|
|
...; |
|||||
|
4 |
|
9 |
|
16 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
3n 1 |
|
|
4n |
|||||||
|
б) |
|
|
|
|
|
|
|
|
|
|
|
; |
|||
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
n 1 |
3n |
|
1 |
|
||||||||||
9. |
а) |
2 |
|
|
4 |
|
|
6 |
|
|
...; |
|||||
|
3 |
|
9 |
|
12 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
3n 1 n2 |
||||||||||
|
б) |
|
|
|
|
|
|
|
|
|
; |
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
n 2 |
3n 2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||
|
|
3 n 2 lnn |
||||||||||||||||||||||||
|
n 2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
г) |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||
|
|
n! n 2 |
|
|
|
|||||||||||||||||||||
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|||||||
|
|
3nlnln n |
|
|
|
|||||||||||||||||||||
|
n 5 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
( 1) |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||
|
3n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
n 0 |
|
|
3 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
n 2 |
|
|
3n lnn |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
г) |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||
|
|
n |
n 3 |
|
|
|
|
|
||||||||||||||||||
|
n 0 |
5 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|||||||
|
|
3n 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
n 2 |
|
|
|
lnn |
|
|
|||||||||||||||||||
|
|
1 n |
|
|
n 5 |
|
|
|||||||||||||||||||
г) |
|
|
. |
|||||||||||||||||||||||
|
3n 6 |
|||||||||||||||||||||||||
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
||||||
|
|
3nln n 2 |
||||||||||||||||||||||||
|
n 2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
1 |
n |
n 1 |
|
|
|
||||||||||||||||||
г) |
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
n 0 |
|
|
|
|
3n 5 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lnn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
в) |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n 2 |
|
|
3 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
г) |
|
|
|
|
|
|
|
. |
|
|
|
|||||||||||||||
|
n 13 |
n |
|
|
||||||||||||||||||||||
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
nln4n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|||||||||||
г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
5n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
n3 |
4n |
||||||||||||||||||||||
|
n 1 |
|
|
|
|
|
||||||||||||||||||||
10
