3.7. Анализ характеристик и параметров цифро-аналогового преобразования сигналов

Цифро-аналоговое преобразование (ЦАП) позволяет на приемном конце системы связи восстановить непрерывные сообщение по принятым двоичным кодовым комбинациямсигнала ИКМ. Это осуществляется с помощью следующих процедур:

а) декодирования – восстановления дискретных - ичных уровнейпо,;

б) интерполяции;

в) низкочастотные фильтрации.

Фильтр – интерполятор – это линейный фильтр с единичной импульсной реакцией на интервале Т (ступенчатая интерполяция) (рис. 7д). ФНЧ сглаживает непрерывно-дискретное сообщение и в результате чего формируется оценка переданного сообщения(см. рис 7е).

Ошибки в двоичном канале связи приводят к несовпадению переданных и принятых кодовых комбинаций сигнала ИКМ. На рис. 7в показана реализация последовательности импульсов ошибок, определяемая как: . Причемприипри.

В декодере ЦАП двоичные ошибки в той или иной позиции кодовой комбинации приводят к несоответствию передаваемых и восстанавливаемых- ичных уровней (см. рис. 7г).

Разность называют ошибкой или погрешностью передачи. Реализации этой погрешности на выходе декодера и на выходе интерполятора приведены на рис. 7д.

Рассмотрим теперь вероятностные характеристики и параметры ДКС и НКС с учетом преобразования сигнала в ЦАП. Так, для определения скорости передачи информации по- ичному ДКС воспользуемся соотношением

,

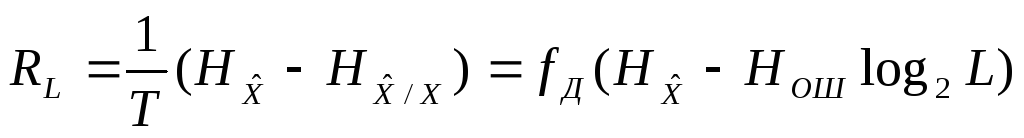(67)

Рис. 7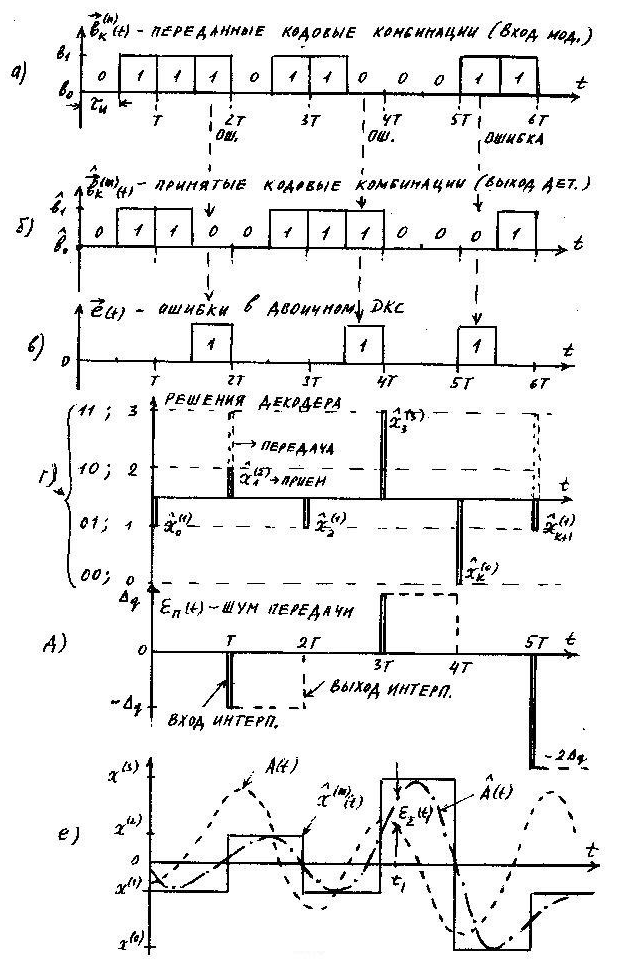

Рис. 7

где – энтропия ошибочных решений в двоичном ДКС, определяемая на (65), а– энтропия восстановленного- ичного сообщения, равная

.

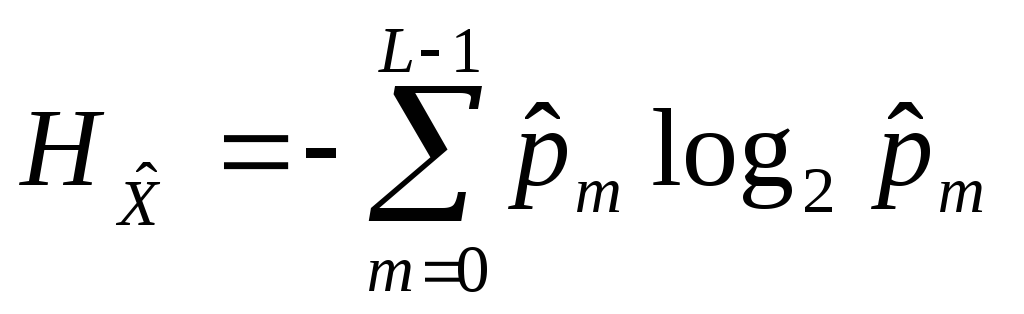(68)

Здесь вероятности , восстановленных уровней передаваемого сообщения равны

.

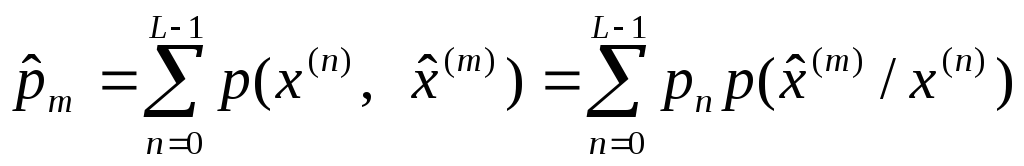(69)

В данном соотношении - распределение вероятностей, определяемое из (16), а условное распределение вероятностей в- ичном ДКС определяется соотношением

.

(70)

где - значность кода,;кодовое расстояние между- й и- й кодовыми комбинациями;

–вероятность ошибки в двоичном симметричном ДКС; – вероятность правильного приема двоичного символа,.

Подставляя (70) в (69), при нетрудно получить следующее соотношение для вероятностей:

.

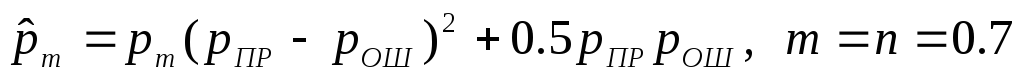(69’)

Зная производительность - ичного источника (скорость ввода информации в ДКС) и скорость передаваемой по ДКС информациинаходим величину относительных потерь в скорости

.

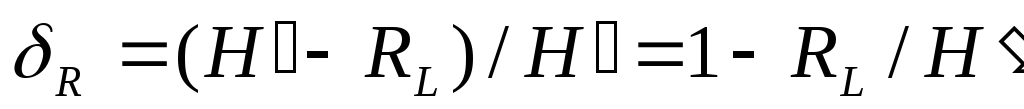(71)

Оценим теперь среднюю квадратическую погрешность шума передачи (СКПП) в- ичном ДКС. Пусть был передан импульс, который на основе соотношения (10) равен. Под действием помех в НКС он может перейти в импульс. Тогда шум передачиможет быть представлен в виде последовательности некогерентных прямоугольных импульсов с нулевым средним и со случайно распределенными амплитудами. На выходе интерполятора длительность этих импульсов совпадает с интервалом дискретизацииТ. Тогда спектр плотности мощности этого шума равен

,

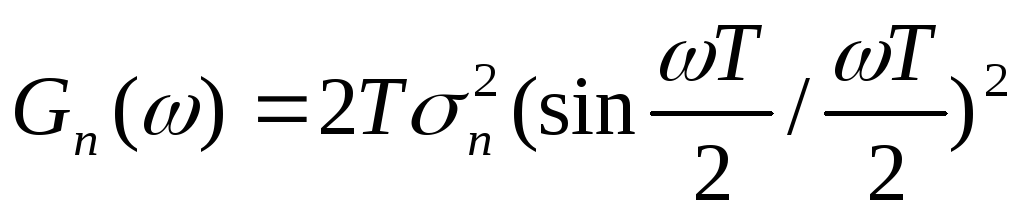(72)

где - дисперсия случайных амплитуд импульсов шума передачи,

.

(73)

Для упрощения расчетов перейдем в (73) к постоянной усредненной величине вероятности ошибки передачи, полагая

.

(74)

где ; - вероятность ошибки в двоичном симметричном ДКС.

Полагая теперь ФНЧ на выходе ЦАП идеальным с полосой пропускания , найдем СКПП интегрированием (72):

.

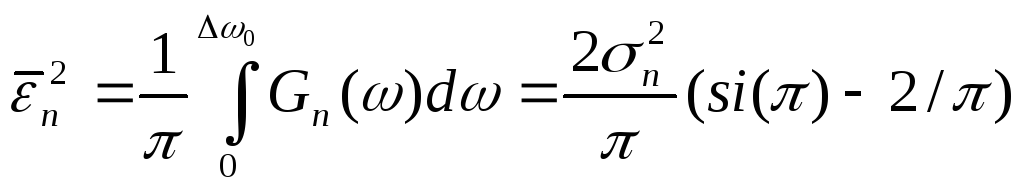(75)

Подставляя (74) и (73) в (75) с учетом (8), получаем соотношение для искомой величины СКПП

,

(75)

где постоянная

;

(76)

- интегральный синус, ;- интегральный закон распределения, определяемый из (18),
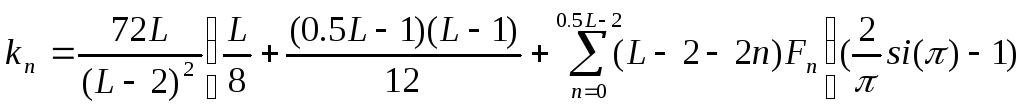