
- •Основные понятия статистики
- •Предмет и метод статистики
- •Статистический показатель: понятие, атрибуты, виды.
- •Сущность и задачи статистического наблюдения
- •Формы, виды и способы статистического наблюдения.
- •7.Статистическая отчетность как форма наблюдения
- •8. Достоверность статистических данных и ошибки статистического наблюдения
- •9. Принципы и правила организации и проведения статистического наблюдения.
- •10. Статистическая сводка и ее место в статистическом анализе
- •11. Статистические группировки и их значение в практическом анализе, порядок построения группировок.
- •12. Виды статистических группировок
- •13. Простые и сложные группировки
- •14. Первичные и вторичные группировки
- •15. Дискретные и интервальные группировки
- •16. Типологические группировки
- •17. Структурные группировки
- •18. Аналитические группировки
- •19. Статистические ряды распределения
- •Кумулятивные ряды распределения – ряды распределения, которые содержат один или оба следующих элемента:
- •20. Статистические таблицы: виды и принципы построения
- •21. Абсолютные показатели, их виды.
- •22. Относительные статистические величины и их виды
- •23. Относительные показатели динамики, показатели плана и реализации плана, связь между ними.
- •24.Относительные показатели сравнения и интенсивности.
- •25.Относительные показатели структуры и координации уровня экономического сравнения.
- •26. Принципы построения относительных показателей. Системы статистических показателей.
- •28. Средняя арифметическая и ее свойства
- •29. Виды степенных средних. Правило мажорантности.
- •30. Медиана и ее практическое значение
- •31. Мода и ее практическое значение
- •32. Показатели вариации и способы их расчета
- •1) Относительный размах вариации:
- •2) Относительное отклонение по модулю:
- •3) Коэффициент вариации
- •33. Правило сложения дисперсий
- •34. Показатель симметричности распределения
- •35. Показатель островершиности распределения
- •36. Нормальное распределение и его свойства
- •38. Сопоставимость статистических величин в рядах динамики
- •37. Понятие о статистических рядах динамики
- •39. Статистические показатели динамики
- •40. Средние показатели ряда динамики
- •41.Анализ закономерностей изменения уровней ряда динамики
- •43. Аналитическое выравнивание динамических рядов
- •44. Анализ сезонных колебаний
- •45. Статистические методы прогнозирования
- •46. Статистические индексы и их виды
- •47. Индивидуальные и сводные индексы
- •48. Агрегатные индексы и их виды
- •49. Средние индексы на основе индивидуальных индексов
- •50. Индексный метод анализа факторов
- •51. Взаимосвязь между индексами переменного, постоянного состава и структурных сдвигов.
- •52. Классификация связей в статистике
- •53. Определение тесноты корреляционной связи
- •54. Понятие регрессии
- •55. Расчет параметров линейного уравнения регрессии мнк
- •56. Понятие о выборочном наблюдении
- •57. Основные способы отбора
- •58. Ошибка выборочного наблюдения при различных способах отбора
- •59. Определение необходимой численности выборки
- •60.Малая выборка. Проверка статистических гипотез.
30. Медиана и ее практическое значение
Медиана (Me) – значение признака, приходящееся на середину ранжированного ряда, т.е. делящее ряд распределения на две равные части.
а) для ряда одиночных значений:
- если нечетное кол-во вариант, то серединное значение в ранжированном ряду
- если четное, то сред.арифмет. из 2х смежных серединных значений в ранжиров. ряду
б) В дискретном ряду распределения определяется номер медианы по формуле:
![]()
Номер медианы показывает то значение показателя, которое и является медианой.
в) В интервальном ряду распределения медиана рассчитывается по следующей формуле:
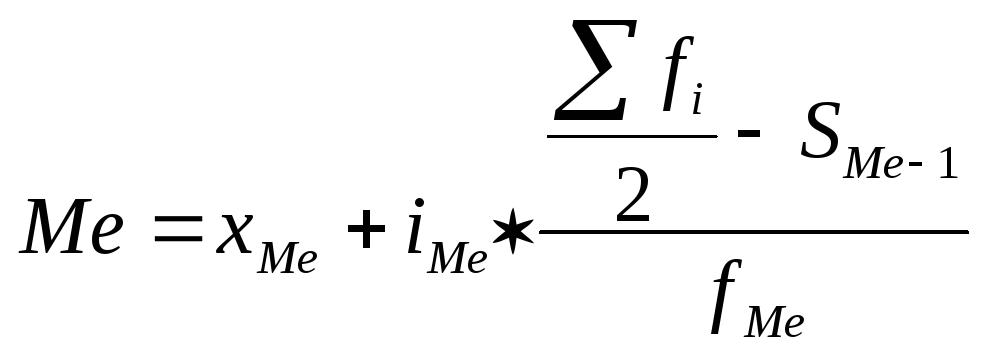
x - нижняя граница медианного интервала;
i - величина интервала;
f - численность медианного интервала;
S - сумма накопленных частот интервалов, предшествующих медианному.
31. Мода и ее практическое значение
Мода (Mo) – величина признака, наиболее часто встречающаяся в совокупности, т.е. имеющая наибольшую численность в ряду распределения.
а) В дискретном ряду распределения мода определяется визуально.
б) В интервальном ряду распределения визуально можно определить только интервал, в котором заключена мода, который называется модальным интервалом(тот, который имеет наибольшую частоту).
Мода будет равна:
![]()
x - нижняя граница модального интервала;
i - величина интервала;
f - численность модального интервала;
Если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды. Если две не соседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называют бимодальным; если таких вариант больше двух, то ряд – полимодальный.
32. Показатели вариации и способы их расчета
Вариации – колеблемость, многообразие, изменяемость величины признака у единиц совокупности.
Показатели вариации делятся на абсолютные и относительные.
К абсолютным показателям относятся размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение. К относительным – коэффициенты осцилляции, коэффициенты вариации и относительное линейное отклонение.
Размах
вариации
– простейший показатель, разность между
максимальным и минимальным значениями
признака.
![]()
Недостатком является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ.
Среднее линейное отклонение отражает все колебания варьирующего признака и представляет собой среднюю арифметическую из абсолютных значений отклонений вариант от средней величины, т.к. сумма отклонений значений признака от средней равно 0, то все отклонения берутся по модулю.
Простая
![]() Взвешенная
Взвешенная![]()
Дисперсия – средний квадрат отклонений значений признака от их средней величины.
Простая:
![]() Взвешенная:
Взвешенная:![]()
Среднее квадратическое отклонение. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность, что и изучаемый признак.
Простая:
![]() Взвешенная:
Взвешенная: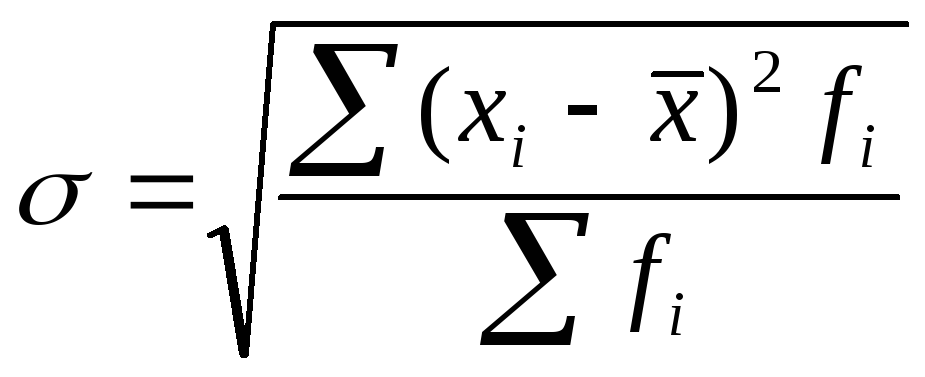 .
.
Относительные показатели
