6.6.3. Защита от шума, электромагнитных полей и излучений

Уровень интенсивности в свободном волновом поле. Уравнение плоской волны, не затухающей с расстоянием, в комплексной форме имеет вид

(6.23)

здесь — комплексная амплитуда; r — радиус-вектор рассматриваемой точки; k — волновой вектор, численно равный волновому числу

где с и  — соответственно скорость распространения и длина волны.

Распространение волны всегда связано с переносом энергии, которая количественно характеризуется мгновенным вектором плотности потока энергии I_t. На практике обычно пользуются понятием интенсивности волны I, которая равна модулю среднего значения вектора I_t за время, равное периоду T полного колебания. Найдем интенсивности звука и электромагнитной волны. Для этого введем понятие импеданса среды при распространении волны.

Комплексным импедансом среды при распространении звуковой волны назовем отношение

где р и v—соответственно звуковое давление и колебательная скорость.

Комплексным импедансом среды при распространении электромагнитной волны назовем отношение поперечных составляющих электрического (Е) и магнитного (H) полей в данной точке:

(6.24)

Положив и̃ ≡ р для звука и ũ ≡ Е̃ для электромагнитного поля, можно для определения интенсивности звуковой волны или для определения интенсивности электромагнитной волны использовать одну и ту же формулу^*:

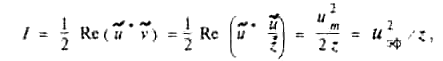(6.25)

где 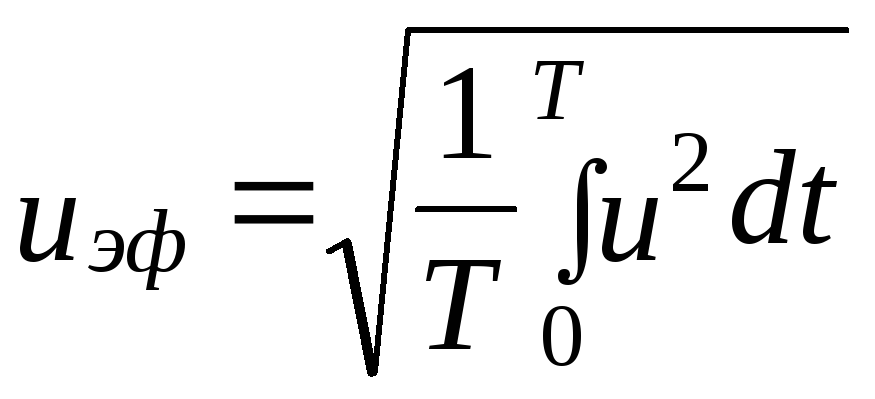— эффективное значение величины и.

При заданных стандартом референтных значениях^** I_*, u_*, z_*, удовлетворяющих условию I_* = u²_*/z_* из соотношения (6.25) следует

L_I = L_u + L_z

Где и—уровни величинI, и, z. Суммарная интенсивность некогерентных источников

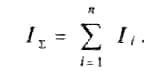
Следовательно, уровень суммарной интенсивности

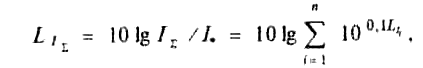
где L_1i и п — соответственно уровень интенсивности i-го источника и число источников. Если все п источников имеют одинаковый уровень интенсивности, равный L_i, то уровень суммарной интенсивности будет равен

Источники направленного действия характеризуют коэффициентам направленности, равным отношению:

где I—интенсивность волны в данном направлении на некотором расстоянии r от источника направленного действия мощностью W, излучающего волновое поле в телесный угол Ω; I_н = W/(4πr²) —интенсивность волны на том же расстоянии при замене данного источника на источник ненаправленного действия той же мощности. В общем случае в сферической системе координат, характеризуемой углами θ и φ, коэффициент направленности ф = = ф(θφ). Для осесимметричных источников коэффициент направленности не зависит от координаты φ и ф = ф(θ). Таким образом, интенсивность можно выразить через мощность источника следующим образом:

При необходимости учесть затухание в уравнение (6.23) вводят вместо волнового числа k комплексное волновое число k̇_*; или коэффициент pаспространения k̂_*:

(6.27)

где  и  — соответственно коэффициент фазы и коэффициент затухания. Амплитуда затухающей волны будет равна u̇_m() = u̇_me^-r, а интенсивность волны будет затухать по закону:

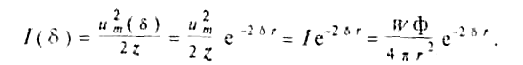
На расстоянии r затухание в децибелах

где ₀ = 8,686 —коэффициент затухания, выраженный в децибелах на единицу длины.

Полагая W_* =I_*S_e, из выражения (6.28) находим уровень интенсивности с учетом затухания:

где S_e и L_v= 10lgW/W_* —соответственно единичная площадь и уровень мощности относительно референтного значения W_*.

Таким образом, уровень интенсивности в данной точке определяется через уровень мощности и коэффициент направленности. Формула (6.29) справедлива в свободном волновом поле, т. е. поле, не имеющем границ, от которых могло бы происходить отражение волн. Свободное поле можно создать и в помещении, если сделать последнее из материала, полностью поглощающего энергию падающей волны. Величину 10lgф называют показателем направленности и обозначают ПН.

Таблица 6.7.

Коэффициент затухания звука в воздухе, дБ/км

Относительная влажность воздуха, %	Среднегеометрические частоты октавных полос, Гц
	125	250	500	1000	2000	4000	8000
10 40 80	0,8 0,4 0,2	1,5 1,3 0,9	3,8 2,8 2,7	12,1 4,9 5,5	40 11 9,7	109 34 21	196 120 66

Для звука коэффициент затухания ₀ зависит от частоты звука, температуры, давления и относительной влажности воздуха. При нормальном атмосферном давлении и температуре воздуха, равной +20 С , значения коэффициента ₀ даны в табл. 6.7. Для электромагнитной волны, распространяющейся в воздухе, ₀  0 (см. ниже). Следует иметь в виду, что в реальных условиях уровень затухания зависит также от погодных условий (дождь, снег, туман и т. д.), наличия растительности (трава, кустарник, деревья и т. д.), состояния атмосферы (ветер, туман, турбулентность, температурные градиенты и т. д.), наличия отражающих поверхностей (земля, преграды, экраны и т. д.) и ряда других факторов и вычисляется по формуле , где e_(i) — уровень затухания при наличии i-го фактора. Если затуханием можно пренебречь ( = 0). то уровень интенсивности:

Диффузное волновое поле в изолированных объемах. Волновое поле называют диффузным, если усредненная по времени объемная плотность энергии w = w_д одинакова во всех точках, а поток энергии через единичную площадку в любой точке и в любом направлении постоянен и равен I_д.

Энергия волны в объеме dV равна d = w_дdV. В диффузном поле эта энергия распределяется равномерно во все стороны пространства 4. Следовательно, на телесный угол d = dSсos/r² приходится часть энергии, равная d² = w_дcosdVdS/4r². В сферической системе координат с полярным углом  элементарный объем dV= r²sindddr и полная энергия через площадку dS найдется в результате следующего интегрирования:

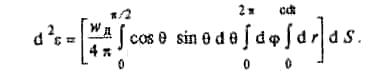
Откуда следует, что поток энергии через единичную площадку

(6.31)

Таким образом, поток энергии через единичную площадку в диффузном волновом поле в четыре раза меньше интенсивности I_в бегущих волн с той же объемной плотностью энергии. Для бегущей со скоростью с волны интенсивность I = cw, где w — усредненная объемная плотность энергии. При наличии диффузного поля понятие интенсивности теряет смысл.

Понятие диффузного поля часто используют при определении плотности потока энергии I_п в изолированных объемах. Под изолированным объемом понимается пространство, огражденное стенками (например, производственное помещение, кабина, пространство под кожухом машины и т. д.). Волны в изолированных объемах, многократно отражаясь, образуют поле, которое изменяется при изменении геометрических размеров, формы и других характеристик источника.

Волновое поле в каждой точке изолированного объема можно представить в виде совокупности волн, непосредственно приходящих в эту точку от источника, именуемую как прямая волна, и совокупности болн, попадающих в нее после отражений от границ изолированного oбъема — отраженная волна.

Плотность энергии w_п в любой точке изолированного объема будет складываться (рис. 6.38) из плотности энергии w прямой волны и плотности энергии w_д при диффузном поле отраженной волны: w_п = w + w_д. Умножив это уравнение на скорость с, получим

I_п = I + 4I_д

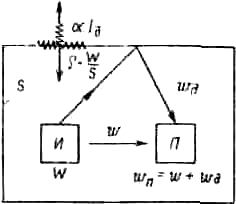
Рис. 6.38. Диффузное поле отраженной волны

Интенсивность прямой волны в общем случае определяется формулой (6.28). Выразим плотность потока энергии I_д через мощность источника. При работе источника в изолированный объем постоянно поступает энергия. При мощности источника W отраженный от границ полный поток энергии составит W, а от единичной площадки W/S. За единицу времени через единичную площадку границы вследствие поглощения исчезнет количество энергии, равное I_д. Так как в диффузном поле плотность энергии постоянная, то должно соблюдаться равенство W/S = I_д. Для простоты дальнейших рассуждений здесь предполагается, что коэффициент  значительно больше коэффициента . Уравнение (6.32) принимает вид

(6.33)

Из полученного выражения видно, что в изолированном объеме плотность потока энергии получает некоторое приращение, которое аналитически обусловлено наличием множителя (1 - )/, который велик при коэффициенте  близком к нулю.

Защитное устройство бесконечной толщины. Во многих случаях информацию можно получить, исследуя вместо реальной конструкции теоретическое защитное устройство бесконечной толщины, оно представляет собой просто среду, бесконечно простирающуюся в направлении распространения волны. Таким образом, волна из одной среды проходит в другую среду (защитное устройство), предварительно попадая на границу раздела этих сред. При падении на плоскую границу раздела двух разных сред плоская волна частично отражается, частично проходит в другую среду, оставаясь плоской, но меняя при этом свое направление распространения, т. е. преломляясь. Таким образом, в общем случае существуют три волны: падающая, отраженная и преломленная (прошедшая).

При прохождении границы раздела сред без поглощения должен соблюдаться закон сохранения энергии: W^- + W^~ = W⁺. Кроме того, на границе должны выполняться специфические для волн данной природы условия: например, для звуковых волн по обе стороны границы должны быть равны звуковые давления — принцип непрерывности звукового давления; для электромагнитных волн на границе раздела двух сред непрерывны тангенциальные составляющие электромагнитного поля. Условие непрерывности при нормальном падении волн можно записать в виде равенства на границе амплитуд поля в среде i и среде j: [u_m]_j = [u_m]_i Усредненный поток энергии можно выразить через интенсивность: W= IS, а интенсивность — через амплитуду и импеданс среды с помощью формулы (6.25). Тогда закону сохранения энергии можно придать вид (рис. 6.39)

где и⁺_m, u^- _т, и u^~ _т — амплитуда, соответственно, падающей, отраженной и прошедшей волн, а z^S_k = z_k/S_k — импеданс на единицу площади (k = i, j).

В среде i существуют падающая и отраженная волна, которые на границе создают суммарную амплитуду [u_m]_j = и⁺_m + и^-_m в среде j существует только преломленная волна: [u_m]_j = u^~_m . Условие непрерывности и закон сохранения энергии позволяют найти амплитудный коэффициент отражения R_ij и амплитудный коэффициент передачи Т_ij при пялении волны на границу (i,j) из среды i:

(6.34)

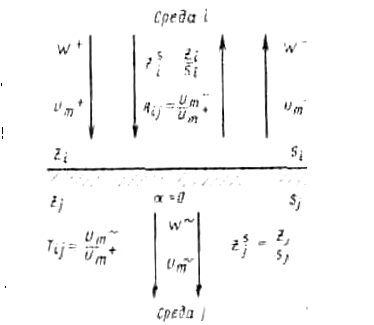
Рис. 6.39. Баланс энергии на границе раздела сред

При этом имеем Т_ij = 1 + R_ij, R_ij = - R_ij . Так как значение коэффициента отражения лежит между -1 и +1, то значение коэффициента передачи заключено в интервале от 0 до 2 и он всегда положителен. При равных площадях (S_i = S_j) соотношения (6.34) примут такой же вид, который можно получить простой заменой z^S_k на z_k а при равных импедансах сред (z_i = z_j) — заменой z^S_k на 1/S_k (k = i, j). Амплитудные коэффициенты отражения и передачи при нормальном падении волн связаны с соответствующими энергетическими коэффициентами соотношениями:

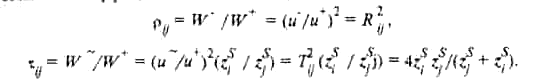
Защитное устройство конечной толщины. В общем случае защитное устройство имеет конечную толщину. При этом волна, падая на защитное устройство, частично отражается, а частично может проходить сквозь него. Отражательную способность защитного устройства характеризуют коэффициентом отражения энергетическим и амплитудным. Прозрачные свойства защитного устройства характеризуют соответствующими коэффициентами передачи. Амплитудные коэффициенты отражения и передачи на границах разных сред будем обозначать соответственно через R_ij и Т_ij. Эти величины определены соотношениями (6.34). Амплитудные коэффициенты отражения и передачи защитного устоойства будем обозначать соответственно чеоез R и Т. при этом в комплексной форме

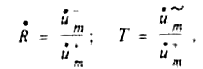
где и— соответственно амплитуда падающей и отраженной волны на входе в защитное устройство; — амплитуда волны на выходе из защитного устройства.

Рассмотрим случай, когда гармоническая волна падает из среды 1 (рис. 6.40) на защитное устройство произвольной толщины h, состоящее из среды 2, ограниченной с другой стороны средой 3, при этом S₁ = S₂ = S₃. Примем, что импедансы сред соответственно равны z₁, z₂ и z₃, а волновое поле в среде 2 на длине h затухает по экспоненциальному закону , гдеk̂_* — коэффициент распространения. При неравных импедансах сред часть энергии на границе (1, 2) отражается обратно в среду 1 в соответствии с формулой (6.34). Амплитуда падающей волны равна и⁺_m. Обозначив амплитуду отраженной волны через u̇₂, имеем: u̇₂ = R₁₂ и̇⁺_m .

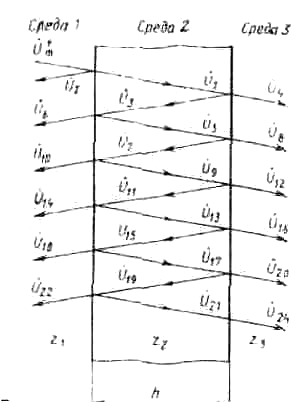
Рис. 6.40. Схема защитного устройства конечной толщины

Другая часть энергии пройдет в среду 2 и, изменившись пропорционально коэффициенту передачи T₁₂ на границе (1, 2), претерпит в среде 2 затухание по закону , так что амплитуда волны в среде2, которую обозначим через u̇₁, определится выражением . Эта волна на границе(2, 3) частично отразится и создаст в среде 2 отраженную волну, амплитуда которой с учетом затухания станет равной и частично пройдет в среду3. Амплитуда прошедшей волны будет pавна . Волна с амплитудойu̇₃ частично пройдет в среду 1: , а частично отразится от границы (1, 2)-и снова будет распространяться в среде 2 в виде волны с амплитудой . Процесс отражения и прохождения волн на границе сред (1,2 и 2, 3) будет продолжаться до полного затухания волн. Суммируя все волны, из которых в среде 1 формируется общая отраженная волна, можно получить для амплитуды этой волны следующее выражение:

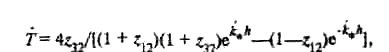(6.37)

где z₁₂ = z₁/z₂ и z₃₂ = z₃/z₂. Полученные соотношения носят общий характер, и их можно применять при решении задач защиты гак от звуковых, так и от электромагнитных полей.

Если по обе стороны от защитного устройства находится одна и та же среда, то импедансы z₁ и z₃ равны. Тогда формулы (6.36) и (6.37) преобразуются к виду:

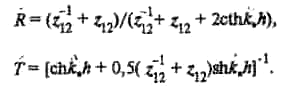
Амплитудные коэффициенты R и Т при нормальном падении волн связаны с энергетическими коэффициентами  и  соотношениями:  = R²,  = Т², эффективность защиты

При распространении звука в атмосфере значение импеданса будет зависеть от температуры и давления. Значение z_* = 400 Пас/м будут соответствовать условиям, когда, например, давление и температура будут соответственно равны 0,910⁵ Па (675 мм рт. ст.) и -27 °С или 1,01310¹⁵ Па и +38,8 °С. Однако при изменении давления и температуры в пределах обычной атмосферы уровень импеданса L_z = 101gz/z_* незначителен и им пренебрегают, полагая, что

Lp( f̂ ) = L_I(f̂) .

Уровень интенсивности или плотности потока энергии можно определить, используя зависимости (6.29), (6.30), (6.33).

Для расчета уровня шума в изолированном объеме используют уравнение (6.33), которое записывают в децибелах в виде

(6.43)

где —уровень плотности потока энергии на сферической поверхности радиуса r, образованной телесным углом излучения  при данном значении постоянной изолированного объема B=S/(1 - ), где S—общая площадь его внутренней поверхности с коэффициентом поглощения; e_ — затухание звука [(см. пояснения к формуле (6.29)], которое в большинстве случаев можно принять равным нулю, S(r) = 4r².

Таблица 6.8.