MOD / mod

Бифуркация Неймарка-Сакера. Это бифуркация рождения

инвариантной кривой. Она имеет место при пересечении верхней границы

треугольника устойчивости. Условие для нахождения этой бифуркации

есть 1 J = . Тогда в соответствии с формулами (29) получаем, что

бифуркация Неймерка-Сакера происходит при −=μ a . Таким образом,

условие бифуркации Неймарка-Сакера не зависит от параметра

дискретизации ε .

Касательная бифуркаций. Эта бифуркация имеет место, когда хотя бы

один из мультипликаторов неподвижной точки становиться равным плюс

единице. Соответственно она имеет место при выходе из треугольника

устойчивости через его правую границу. Условие для нахождения этой

бифуркации имеет вид

− S + J = 01 .

Подставив в это уравнение выражения для следа и якобиана (29) получим,

что касательная бифуркация имеет место при 0 a = . Это полностью

соответствует бифуркации седло-узел в осцилляторе-прототипе.

Седлоузловая бифуркация

В теории динамических систем, седлоузловая бифуркация — локальная бифуркация, при которой пара особых точек (устойчивая и неустойчивая) сливаются в полуустойчивую особую точку (седлоузел), затем исчезающую. Единственная бифуркация, которая встречается в типичных однопараметрических семействах векторных полей на прямой неустранимым образом (т.е. является типичной бифуркацией коразмерности 1).

[править]Нормальная форма

анимация  [показать]

Рассмотрим векторное поле на прямой, имеющее особую точку. Если особая точка невырождена (производная векторного поля в ней отлична от 0), по теореме о неявной функции, она сохраняется при малых возмущениях, и бифуркации не происходит. Таким образом, простейший случай, интересный с точки зрения теории бифуркаций: первая производная равна нулю. В типичном случае, вторая производная ненулевая. Раскладывая векторное поле в ряд Тейлора и меняя при необходимости систему координат, можно считать, что коэффициент при  равен -1. В этом случае векторное поле имеет вид:

Поскольку особая точка вырождена, векторное поле (1) не является структурно устойчивым: сколь угодно малым возмущением можно уничтожить особую точку или «развалить» её на две. Оказывается, любое невырожденное малое возмущение этого векторного поля в окрестности особой точки 0 (топологически) эквивалентно однопараметрическому семейству

Иными словами, это семейство будет версальной деформацией для уравнения (1). Семейство (2) является нормальной формой седлоузловой бифуркации.

[править]Сценарий бифуркации

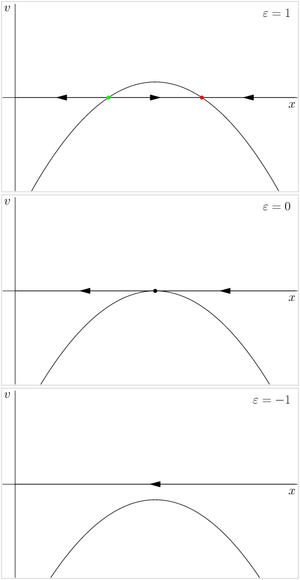
Рассмотрим семейство (2). Возможно три случая:

• При 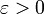 векторное поле имеет две особые точки: . Одна из них () является устойчивой, другая (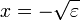) — неустойчивой.

• При  векторное поле имеет единственную полуустойчивую негиперболическую особую точку 0.

• При 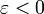 векторное поле не имеет особых точек.

Таким образом, седлоузловая бифуркация может быть описана как процесс рождения полуустойчивой особой точки и последующего её распадения на устойчивую и неустойчивую, или наоборот — как процесс слияния устойчивой и неустойчивой особой точки в полуустойчивую с последующим её исчезновением.

Седлоузловая бифуркация на плоскости: }

Если рассматривать двумерное фазовое пространство и к уравнению (2) добавить уравнение , при , особая точка  будет устойчивым узлом, а особая точка  — седлом. Сливаясь при , они образуют особую точку с одним нулевым и одним ненулевым собственным значением, то есть седлоузел. Это и объясняет название бифуркации.

неподвижная точка отображения — точка, которую отображение переводит в неё же, иными словами, решение уравнения .

К примеру, отображение  имеет неподвижные точки  и , поскольку  и .

Неподвижные точки есть не у всякого отображения — скажем, отображение  вещественной прямой в себя неподвижных точек не имеет.

Точки, возвращающиеся в себя после определённого числа итераций, то есть, решения уравнения

называются периодическими (в частности, неподвижные точки — это периодические точки периода 1).

Притягивающие неподвижные точки

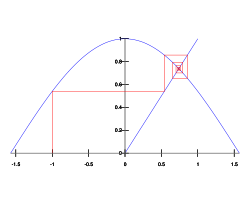
Нахождение решения уравнения x=cos x

Неподвижная точка x=f(x) отображения f — притягивающая, если итерации любой начальной точки y, достаточно близкой к x, будут к x стремиться:

(При этом, обычно, требуют, чтобы итерации y не покидали некоторой большей окрестности точки x — то есть, чтобы точка x была асимптотически устойчива.)

В частности, достаточным условием, чтобы точка была притягивающей, является условие на производную: |f'(x)|<1.

Метод Ньютона

Одним из применений идеи притягивающей неподвижной точки является метод Ньютона: искомое решение оказывается притягивающей неподвижной точкой построенного отображения, и потому может быть найдено как предел (очень быстро сходящейся) последовательности итераций.

Наиболее известное применение этого метода нахождение квадратного корня из числа a>0 как последовательности итераций отображения

Устойчивость неподвижных точек одномерного отображения

     Рассмотрим методику определения устойчивости неподвижных точек отображения (14.2). Если значение  находится в окрестности неподвижной точки , справедливо равенство:

(14.5)

где  - малая величина. Если точка  устойчива, то с ростом номера последовательности n величина  должна уменьшаться. Запишем соотношение (14.2) с учётом (14.5) и разложим правую часть в ряд Тейлора:

Последнее приближённое равенство выполняется тем точнее, чем меньше . С учётом (14.3) получим:

Следовательно, для того чтобы  должно выполняться неравенство:

(14.6)

Это и есть условие устойчивости неподвижных точек  отображения (14.2).       Определим, при каких значениях параметра  будут устойчивы неподвижные точки (14.4). Производная от функции f (x) отображения (14.2) равна:

     Для неподвижной точки  имеем:

Следовательно, точка  действительно устойчива при  < 1.       Для неподвижной точки  получаем:

Следовательно, точка  будет устойчива для значений параметра

При  > 3 неподвижная точка  теряет устойчивость.

Понятие бифуркации

Исследуемый реальный процесс протекает обычно при определённых внешних условиях, которые в общем случае можно охарактеризовать определёнными значениями параметров системы. Эти параметры входят также и в соответствующую систему дифференциальных уравнений. Таким образом, математическая модель принимает вид: где  - вектор параметров системы.       Определение. Качественное изменение фазового портрета, происходящее при изменении параметра системы , называется бифуркацией фазового портрета. Значение параметра системы  = 0, при котором происходит бифуркация, называется бифуркационным значением параметра (или точкой бифуркации).      Например, имеем уравнение:   (11.1) характеризующее динамику цепной реакции при  > 0 и распада ядра при  < 0. На рисунке представлен фазовый портрет уравнения (11.1) при  < 0 и  > 0. Видно, что при  < 0неподвижная точка  - аттрактор, а при  > 0 - репеллер. Когда  возрастает, проходя через нуль, то решение из убывающего превращается в возрастающее. Таким образом,  = 0 - точка бифуркации.       На практике наиболее часто встречаются три типа бифуркаций: бифуркация типа седло-узел, бифуркация Андронова-Хопфа и бифуркация с удвоением периода.