2.6. Сетевые модели (n-схемы)

В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом при­чинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов. Самым распростра­ненным в настоящее время формализмом, описывающим структуру и взаимодействие параллельных систем и процессов, являются сети Петри (англ. Petri Nets), предложенные К. Петри [28, 30].

Основные соотношения. Теория сетей Петри развивается в нес­кольких направлениях: разработка математических основ, структур­ная теория сетей, различные приложения (параллельное програм­мирование, дискретные динамические системы и т. д.).

Формально сеть Петри (N-схема) задается четверкой вида

где В — конечное множество символов, называемых позициями, В ≠Ø; D — конечное множество символов, называемых перехода­ми, D≠Ø, В ∩D ≠Ø ; I—входная функция (прямая функция ин­цидентности), I: ВхD→-{0, 1}; О — выходная функция (обратная функция инцидентности), О : D х В→ {0,1}. Таким образом, входная функция отображает переход d_j в множество входных позиций bi € I(dj), а выходная функция О отображает переход dj в множество выходных позиций b_{i €} D(dj). Для каждого перехода

d_i€ D можно определить множество входных позиций перехода I(dj) и выходных позиций перехода О(d_j) как

Аналогично, для каждого перехода b_i€В вводятся определения множества входных переходов позиции I(b_i) и множества выходных переходов позиции I(b_i):

Графически N-схема изображается в виде двудольного ориентированного мультиграфа, представляющего собой совокупность позиций и переходовние N-схемы (рис. 2.8). Как видно из этого рисунка ,граф N-схемы имеет два типа узлов :позиции и переходы, изображаемые 0 и 1 соответственно. Ориен­тировочные дуги соединяют позиции и переходы, причем каждая дуга направлена от элемента одного множества (позиции или пере­хода) к элементу другого множества (переходу или позиции). Граф N-схемы является мультиграфом, так как он допускает существова­ние кратных дуг от одной вершины к другой.

Пример 2.7. Представим формально N-схему, показанную в виде графа на рис. 2.7:

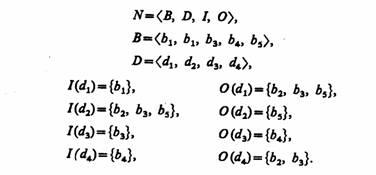
Возможные приложения. Приведенное представление N-схемы может использоваться только для отражения статики моделиру­емой системы (взаимосвязи событий и условий), но не позволяет отразить в модели динамику функционирования моделируемой си­стемы. Для представления динамических свойств объекта вводится функция маркировки (разметки) М: В→{О, 1, 2, ...}. Маркировка М есть присвоение неких абстрактных объектов, называемых мет­ками (фишками), позициям N-схемы, причем количество меток, соответствующее каждой позиции, может меняться. При графичес­ком задании N-схемы разметка отображается помещением внутри вершин-позиций соответствующего числа точек (когда количество точек велико, ставят цифры).

Маркированная (размеченная) N-схема может быть описана в виде пятерки N_M = ‹B, D, I, О, М› и является совокупностью сети Петри и маркировки М [28, 30].

Функционирование N-схемы отражается путем перехода от раз­метки к разметке. Начальная разметка обозначается как М_о : В→ {0, 1, 2, ...}. Смена разметок происходит в результате срабатывания

одного из переходов dj εD сети. Необходимым условием срабатыва­ния перехода dj является b_tel(dj) {M(bi)^l}, где M{b_t} — разметка позиции Ь_г. Переход d_h для которого выполняется указанное усло­вие, определяется как находящийся в состоянии готовности к сраба­тыванию или как возбужденный переход.

Срабатывание перехода dj изменяет разметку сети М(b) = =(M(b₁), M(b₂), ..., M(b_n))² на разметку М'(b) по следующему правилу:

т. е. переход dj изымает по одной метке из каждой своей входной позиции и добавляет по одной метке в каждую из выходных пози­ций. Для изображения смены разметки М на М' применяют обозна­чение М |^dj_М'.

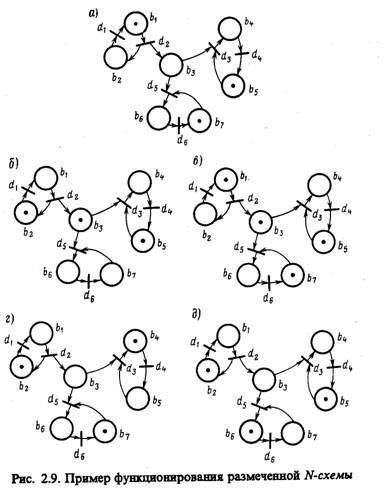
Пример 2.8. Рассмотрим размеченную N-схему с начальной разметкой М_о={1, 0, 0, 0, 1, 0, 1}, которая приведена на рис. 2.9, а. При такой начальной разметке N-схемы единственным готовым к срабатыванию является переход d₂, срабатывание

которого ведет к смене разметки М_о |-² М₁, где M₁ = {0, 1, 1, 0, 1, 0, 1} (рис. 2.9, б). При разметке М₁ возможно срабатывание переходов d_1, d₃ и d₅. В зависимости от того, какой переход сработал первым, получается одна из трех возможных новых маркировок (рис. 2.9, в, г. д). Функционирование N-схемы продолжается до тех пор, пока существует хотя бы один возможный переход.

Таким образом, N-схема выполняется путем запусков перехо­дов под управлением количества меток и их распределения в сети. Переход запускается удалением меток из его входных по­зиций и образованием новых меток, помещаемых в выход­ные позиции. Переход может запускаться только тогда, когда он разрешен. Переход называется разрешенным, если каждая из его входных позиций имеет число меток, по крайней мере равное числу дуг из позиции в переход.

Пример 2.9. Для некоторой заданной размеченной N-схемы (ряс. 2.8) с начальной маркировкой М_о = {1, 2, О, 0, 1} (рис. 2.10, а) разрешенным является только переход d_1, а остальные переходы d₂, d₃ и d₄ — запрещен­ные. В результате выполнения этого перехода получим новую размеченную N-схему (рис. 2.10, б). Теперь разрешены переходы d₂ и d_%; в результате их запуска получим новую раз­меченную N-схему. Переходы d₂ и d₃ нахо­дятся в конфликте, так как запущен, может быть только один из них. Например, при запуске d₃ получим сеть, показанную на рис. 210, в. Теперь разрешен только переход d₄. и получим новую размеченную сеть (рис. 2.10, г). Теперь разрешено два перехода: d₂ и d₃ (в конфликте). Запустим переход d₂ (рис. 2.10, д). Теперь ни один переход не может быть запу­щен и выполнение сети прекращается.

Важной особенностью "моделей процесса функционирования систем с использованием типовых N-схем является простота построения ие­рархических конструкций модели. С одной стороны, каждая N-схема может рассматриваться как макро­переход или макропозиция модели более высокого уровня. С другой стороны, переход, или позиция N-схемы, может детализироваться в форме отдельной подсети для бо­лее углубленного исследования про­цессов в моделируемой системе. Отсюда вытекает возможность эффективного использования N-схем для моделирования параллельных и конкурирующих процессов в различных системах.

Типовые N-схемы на основе обычных размеченных сетей Петри пригодны для описания в моделируемой системе S событий произ­вольной длительности. В этом случае модель, построенная с ис­пользованием таких N-схем, отражает только порядок наступления событий в исследуемой системе S. Для отражения временных пара­метров процесса функционирования моделируемой системы S на базе N-схем используется расширение аппарата сетей Петри: вре­менные сети, ii-сети, сети Мерлина и т. д. [19]. Детально вопросы, связанные с имитационным моделированием с использованием N-схем, будут рассмотрены далее.

77777777777777777777777777777777777777777777777777777777777777777777777777777777777

Конгруэнтные процедуры генерации. Широкое применение при моделировании систем на ЭВМ получили конгруэнтные процедуры генерации псевдослучайных последовательностей, представляющие собой арифметические операции, в основе которых лежит фунда­ментальное понятие конгруэнтности. Два целых числа а и β конгру­энтны (сравнимы) по модулю т, где т — целое число, тогда и толь­ко тогда, когда существует такое целое число к, что a— β =km, т. е. если разность а— β делится на т и если числа α и β дают одинаковые остатки от деления на абсолютную величину числа т. Например, 1984=4 (mod 10), 5008 = 8 (mod 10³) и т. д.

Конгруэнтные процедуры являются чисто детерминированны­ми, так как описываются в виде рекуррентного соотношения, когда функция (4.9) имеет вид

Если заданы начальное значение Х₀, множитель λ и аддитивная константа μ, то (4.11) однозначно определяет последовательность целых чисел {X_i}, составленную из остатков от деления на М членов последовательности {λⁱX₀ + μ(λⁱ - 1)/(λ - 1)}. Таким образом, для любого i ≥ 1 справедливо неравенство X_i < M. По целым числам последовательности {X_i} можно построить последовательность {х_i} = {X_i/M} рациональных чисел из единичного интервала (0, 1).

Конгруэнтная процедура получения последовательностей псевдослучайных квазиравномерно распределенных чисел может быть реализована мультипликативным либо смешанным методом.

88888888888888888888888888888888888888888888888888888888888888888888888888888888888

Мультипликативный метод. Задает последовательность неотрицательных целых чисел {X_i}, не превосходящих М, по формуле

т. е. это частный случай соотношения (4.10) при μ= 0.

В силу детерминированности метода получаются воспроизводимые последовательности. Требуемый объем машинной памяти при этом минимален, а с вычислительной точки зрения необходим последовательный подсчет произведения двух целых чисел, т. е. выполнение операции, которая быстро реализуется современными ЭВМ.

Для машинной реализации наиболее удобна версия М = р^g, где р - число цифр в системе счисления, принятой в ЭВМ (р = 2 для двоичной и р = 10 для десятичной машины); g - число битов в машинном слове. Тогда вычисление остатка от деления на М сводится к выделению g младших разрядов делимого, а преобразование целого числа Х_i в рациональную дробь из интервала х_i ∈ (0, 1) осуществляется подстановкой слева от X_i, двоичной или десятичной запятой.

Алгоритм построения последовательности для двоичной машины М = 2^g сводится к выполнению таких операций [31, 36, 46]:

1. Выбрать в качестве Х₀ произвольное нечетное число.

2. Вычислить коэффициент λ = 8t ± 3, где t - любое целое положительное число.

3. Найти произведение λХ₀, содержащее не более 2g значащих разрядов.

4. Взять g младших разрядов в качестве первого члена последовательности X₁, а остальные отбросить.

5. Определить дробь х₁ = Х₁/2^g из интервала (0, 1).

6. Присвоить Х₀ = Х₁.

7. Вернуться к п. 3.

Пример 4.4. Необходимо получить числа последовательности для случая g = 4, используя приведенный алгоритм мультипликативного метода. Для этого выполняем следующие действия: 1. Выбираем Х₀₁₀ = 7 (в десятичной системе счисления) или Х₀ = 0111 (в двоичной системе счисления). 2. Найдем t = 1, тогда λ₁₀ = 11 или 5; пусть λ₁₀ = 5, λ = 0101. 3. Рассчитываем произведение λХ₀, берем g младших разрядов, вычисляем Х₁ и присваиваем Х₀ = Х₁, т. е. выполняем п. 3 - 7 алгоритма:

99999999999999999999999999999999999999999999999999999999999999999999999999999999999

Смешанный метод. Позволяет вычислить последовательность неотрицательных целых чисел {Х_i}, не превосходящих М, по формуле

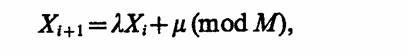
т. е. в отличие от мультипликативного метода μ ≠ 0 вычислительной точки зрения смешанный метод генерации сложнее мультипликативного на одну операцию сложения, но при этом возможность выбора дополнительного параметра позволяет уменьшить возможную корреляцию получаемых чисел.

Качество конкретной версии такого генератора можно оценить только с помощью соответствующего машинного эксперимента.

В настоящее время почти все пакеты прикладных программ универсальных ЭВМ для вычисления последовательностей равномерно распределенных случайных чисел основаны на конгруэнтной процедуре [17, 38, 40].

10101010101010101010101010101010101010101010101010101010101010101010101010101010101

Проверка равномерности последовательностей псевдослучайных квазиравномерно распределенных чисел {х_i} может быть выполнена по гистограмме с использованием косвенных признаков [4, 26]. Суть проверки по гистограмме сводится к следующему. Выдвигается гипотеза о равномерности распределения чисел в интервале (0, 1). Затем интервал (0, 1) разбивается на m равных частей, тогда при генерации последовательности {х_i} каждое из чисел х с вероятностью p_j = 1/m, j = 1, т, попадает в один из подынтервалов. Всего в каждый j-й подынтервал попадает N_j чисел последовательности {х_i}, i = 1, N, причем N =

N_j. Относительная частота попадания случайных чисел последовательности {х_i} в каждый из подынтервалов будет равна N_j/N. Вид соответствующей гистограммы для примера показан на рис. 4.11, а, где пунктирная линия соответствует теоретическому значению p_j, а сплошная - экспериментальному N_j/N. Очевидно, что если числа х_i - принадлежат псевдослучайной квазиравномерно распределенной последовательности, то при достаточно больших N экспериментальная гистограмма (ломаная линия на рис. 4.11, а) приблизится к теоретической прямой 1/т.

Оценка степени приближения, т. е. равномерности последовательности {х_i}, может быть проведена с использованием критериев согласия. На практике обычно принимается т = 20 ÷ 50, N = (10² ÷ 10³)m.

Суть проверки равномерности по косвенным признакам сводится к следующему. Генерируемая последовательность чисел {х_i} разбивается на две последовательности:

Затем проводится следующий эксперимент. Если выполняется условие

то фиксируется наступление некоторого события и в счетчик событий добавляется единица. После N/2 опытов, когда генерировано N число, в счетчике будет некоторое число k ≤ N/2.

Геометрически условие (4.13) означает, что точка (х_{2i - 1}, х_2i) = 1, N, находится внутри четверги круга радиусом r = 1, что иллюстрируется рис. 4.11, б. В общем случае точка (х_{2i - 1}, х_2i) всегда попадает внутрь единичного квадрата. Тогда теоретически вероятность попадания этой точки в четверть круга

Если числа последовательности {х_i} равномерны, то в силу закона больших чисел теории вероятностей при больших N относительная частота 2k/N → π/4.

11111111111111111111111111111111111111111111111111111111111111111111111111111111111

Проверка стохастичности последовательностей псевдослучайных чисел {х_i} наиболее часто проводится методами комбинаций и серий [7, 11, 25]. Сущность метода комбинаций сводится к определению закона распределения длин участков между единицами (нулями) или закона распределения (появления) числа единиц (нулей) в n-разрядном двоичном числе X_i. На практике длину последовательности N берут достаточно большой и проверяют все п разрядов или только l старших разрядов числа X_i.

Теоретически закон появления j единиц в l разрядах двоичного числа X_i описывается исходя из независимости отдельных разрядов биномиальным законом распределения:

где P (j, l) - вероятность появления j единиц в l разрядах числа Х_i; p(1) = p(0) = 0,5 - вероятность появления единицы (нуля) в любом разряде числа Х_i; C^j_l = l!/[j!/(l - j)!].

Тогда при фиксированной длине выборки N теоретически ожидаемое число появления случайных чисел Х_i с j единицами в проверяемых l разрядах будет равно n_j = NC^j_l p^l (1).

После нахождения теоретических и экспериментальных вероятностей P (j, l) или чисел n_j при различных значениях l ≤ n гипотеза о стохастичности проверяется с использованием критериев согласия [7, 11, 18, 21].

При анализе стохастичности последовательности чисел {х_i} методом серий последовательность разбивается на элементы первого и второго рода (а и b), т. е.

где 0 < р < .

Серией называется любой отрезок последовательности, состоящий из идущих друг за другом элементов одного и того же рода, причем число элементов в отрезке (а или b) называется длиной серии.

После разбиения последовательности {х_i} на серии первого и второго рода будем иметь, например, последовательность вида

...aabbbbaaabaaaabbbab... .

Так как случайные числа а и b в данной последовательности независимы и принадлежат последовательности {х_i}, равномерно распределенной на интервале (0, 1), то теоретическая вероятность появления серии длиной j в последовательности длиной l в N опытах (под опытом здесь понимается генерация числа х_i и проверка условия х_i < p) определится формулой Бернулли:

В случае экспериментальной проверки оцениваются частоты появления серий длиной j. В результате получаются теоретическая и экспериментальная зависимости P(j, l), сходимость которых проверяется по известным критериям согласия, причем проверку целесообразно проводить при различных значениях р, 0 < р < 1 и l.

12121212121212121212121212121211212121212121212121212121212121212121212121212121212

Проверка независимости элементов последовательности псевдослучайных квазиравномерно распределенных чисел проводится на основе вычисления корреляционного момента [4].

Случайные величины ξ и η называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. Таким образом, независимость элементов последовательности {х_i} может быть проверена путем введения в рассмотрение последовательности {y_j} = {x_i+τ}, где τ - величина сдвига последовательностей.

В общем случае корреляционный момент дискретных случайных величин ξ и τ с возможными значениями х_i и y_j определяется по формуле

где p_ij - вероятность того, что (ξ, η) примет значение (х_i, y_j).

Корреляционный момент характеризует рассеивание случайных величин ξ и η и их зависимость. Если случайные числа независимы, то K_ξη = 0. Коэффициент корреляции

где σ_х—σ_y— средние квадратические отклонения величин ξ и η.

При проведении оценок коэффициента корреляции на ЭВМ удобно для вычисле­ния использовать следующее выражение

При любом τ ≠ 0 для достаточно больших N с доверительной вероятностью β справедливо соотношение

Если найденное эмпирическое значение Р ζητ (τ) находится в ука­занных пределах, то с вероятностью β можно утверждать, что полученная последовательность чисел {х,) удовлетворяет гипотезе корреляционной независимости.

13131313131313131313131313131313131313131313131313131313131313131313131313131313131

Неравенство Чебышева. Для неотрицательной функции g (ζ) случайной величины ζ и любого К> 0 выполняется неравенство

Теорема Бернулли. Если проводится N независимых испытаний, в каждом из которых некоторое событие А осуществляется с вероятностью р, то относительная частота появления события m/'N при N→oo сходится по вероятности к р, т. е. при любом ε >0

где т — число положительных исходов испытания.

Теорема Пуассона. Если проводится N независимых испытаний н вероятность осуществления события А в i-м испытании равна p_i,-, то относительная частота появления события m/N при N-→ оо сходится по вероятности к среднему из вероят­ностей p_i т. е. при любом ε >0

Теорема Чебышева. Если в N независимых испытаниях наблюдаются значения x_lt .... х_к случайной величины ζ, то при N-→co среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию а, т. е. при любом ε>0

Обобщенная теорема Чебышева. Еслиζ₁, ..., ζ_n— независимые случайные вели­чины с математическими ожиданиями а_1г ..., a_N и дисперсиями. σ₁., σ_n, ограничен­ными сверху одним и тем же числом, то при N→00 среднее арифметическое значений случайной величины сходится по вероятности к среднему арифметическому их математических ожиданий:

Теорема Маркова. Выражение (4.6) справедливо и для зависимых случайных величин ζ₁,..., ζ_n если только

Совокупность теорем, устанавливающих устойчивость средних показателей, при­нято называть законом больших чисел.

14141414141414141414141414141414141414141414141414141414141414141414141414141414141