
Кочура_lab1 / gershkovich-yu-b-shirokov-k-a-primenenie-paketa-matlab-dlya-resheniya-
.pdfФедеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
Российский государственный университет нефти и газа имени И.М. Губкина
Кафедра автоматизации технологических процессов
Гершкович Ю.Б., Широков К.А.
Применение пакета “MATLAB”для решения нелинейных задач оптимизации градиентными методами.
Методические указания для семинаров по дисциплине “Оптимизация и оптимальное управление технологическими процессами” для студентов специализации 210205 – автоматизация технологических
процессов и производств в нефтяной и газовой промышленности.
Москва, 2009
УДК 681.5 ББК 32.965
Гершкович Ю.Б., Широков К.А. Применение пакета “MATLAB”для решения нелинейных задач оптимизации градиентными методами. М.: РГУ нефти и газа имени И.М.Губкина, 2009г.
Методические указания для семинаров по дисциплине “Оптимизация и оптимальное управление технологическими процессами” для студентов специализации 210205 – автоматизация технологических процессов и производств в нефтяной и газовой промышленности посвящены градиентным методам решения нелинейных задач математического программирования и их реализации в среде современных компьютерных технологий – пакете “MATLAB”. Для каждого рассматриваемого метода приводятся блок – схема алгоритма, программа на языке “MATLAB” и графическая иллюстрация движения точки к экстремуму. Материалы этой работы могут быть рекомендованы для дипломного проектирования, при подготовке выпускных работ в бакалавриате и магистратуре.
Рецензент – к.т.н. доцент Д.Н.Великанов (РГУ нефти и газа имени И.М.Губкина)
Гершкович Ю.Б., Широков К.А.
Российский государственный университет нефти и газа имени И.М. Губкина, 2009.
2
СОДЕРЖАНИЕ Введение………………………………………………………………..4 1.Задачи безусловной оптимизации…………………………………..5
1.1.Метод покоординатного спуска………………………………..6
1.2.Методы одновременного вычисления
координат следующей точки……………………………………6
1.2.1.Градиентный метод с постоянным шагом…………………….6
1.2.2.Градиентный метод с дроблением шага……………………....6
1.2.3.Градиентный метод наискорейшего спуска…………………..9
Сравнение методов……………………………………………………10
2.Градиентные методы в задачах с ограничениями………………..11
2.1.Метод линеаризации целевой функции (Франка – Вульфа)….11
2.2.Метод штрафных функций с постоянным коэффициентом штрафа……………………………………………………………16
2.3.Метод Эрроу-Гурвица…………………………………………...17 Сравнение методов……………………………………………………..22 Приложение……………………………………………………………. 23 1. Некоторые замечания по реализации алгоритмов
всреде “MATLAB”………………………………………………….23 2. Блок-схема алгоритма покоординатного спуска………………….24
Пример реализации метода покоординатного спуска в среде
«MATLAB»………………………………………………………….24 3. Блок-схема алгоритма с постоянным шагом………………………26
Пример реализации метода с постоянным шагом в среде
“MATLAB”…………………………………………………………..26 4. Блок-схема алгоритма метода с дроблением шага………………..28
Пример реализации метода с дроблением шага в среде
“MATLAB”…………………………………………………………..29 5. Блок-схема алгоритма метода наискорейшего спуска……………30
Пример реализации метода наискорейшего спуска в среде
“MATLAB”…………………………………………………………..31 Литература………………………………………………………………32
3

Введение.
Градиентные методы решения задач вогнутого программирования являются вычислительными методами поиска экстремума. Они применимы к классу вогнутых, дифференцируемых функций f(x), определенных на выпуклом допустимом множестве Х. Здесь х = ( x1 ,....xn ) - вектор,
принадлежащий n-мерному векторному пространству, x X . Вычислительные методы применяются в том случае, когда стандартная процедура решения нелинейных задач вогнутого программирования приводит к необходимости решать систему неравенств Куна – Таккера [1], для решения которой не существует регулярных методов.
Все вычислительные методы устроены по единой схеме. Задается начальная точка х0 , как правило из допустимого множества Х, и выбирается направление движения из этой точки, по которому добираемся до следующей точки х1 . Для дифференцируемых функций естественно выбрать направление максимального возрастания целевой функции f(x), т.е. двигаться от точки к точке в направлении вектора-градиента
0 = dfdх(x0 ) =(∂∂xf1 (x0 ),....∂∂xfn (x0 ) . Процедура вычисления значения
следующей точки называется итерацией. В градиентных методах точка х1 вычисляется по правилу х1 = х0 + γ0 0 , где γ0 - значение шага на первой
итерации. Далее необходимо убедиться в том, что новая точка х1 не является точкой решения нашей задачи, т.е. точкой максимума целевой функции. Для этого необходимо проверить правило «останова» алгоритма. Правило «останова» зависит от того, какую задачу мы решаем. Если Х = Rn, т.е. - ∞<хj<∞, j =1,…n, то мы решаем задачу безусловной оптимизации, и в точке максимума норма вектора – градиента не должна превосходить заданной
величины δ - точности метода: k = ∑n |
( f j′)2 k ≤δ . |
(1) |
j =1 |
|
|
В задачах безусловной оптимизации в точке х* экстремума целевой функции норма вектора-градиента в случае точного решения равна нулю, т.е. х*=( x j *, j =1,...n ) есть решение системы уравнений (2):
(x*) ≡0, f j′(x*) =0, j =1,...n. |
(2) |
Поэтому принято называть градиентные методы методами «спуска» к нулю нормы вектора-градиента.
Если же допустимое множество Х задано, то в точке решения (если она на границе) норма вектора –градиента может быть любая, и правило останова выбирают, ограничивая приращение целевой функции на двух смежных итерациях.
4
Итак, основное правило градиентных методов для двух смежных точек :
(x j )k +1 |
=(x j )k +γk k , |
(3) |
где |
k - значение вектора-градиента целевой функции на предыдущей |
|
итерации. |
|
|
Градиентные методы безусловной оптимизации в задачах вогнутого программирования отличаются друг от друга способом движения к максимуму и способом выбора шага. Градиентные методы для решения задач с ограничениями применяются в блочных алгоритмах, где каждый блок использует результаты решения более простых задач, рассмотренных ранее.
1. Задачи безусловной оптимизации.
Градиентные методы в задачах безусловной оптимизации по способу движения к максимуму можно разделить на две группы. В первой группе на (к+1)-ой итерации последовательно, одна за другой, вычисляются координаты вектора (к+1)- ой точки (методы покоординатного спуска). Во второй группе все координаты (к+1)-ой точки вычисляются сразу [2]. В любом из этих методов можно
применять различные способы выбора шага γ k . Наиболее распространенными способами выбора шага являются следующие:
1)Постоянный шаг – задается (угадывается) до решения задачи в том случае, когда скорость решения (количество итераций) не существенно.
2)Переменный шаг – метод «дробления шага» - используется в том случае, когда заданный в начале алгоритма шаг «проскакивает» максимум, и норма вектора-градиента начинает расти.
3)Метод наискорейшего спуска – на каждой итерации вычисляется значение шага, максимизирующее целевую функцию на текущей итерации.
Вдальнейшем приводится решение задачи безусловной оптимизации различными методами. Указания по программированию в пакете “MATLAB”, блок-схемы алгоритмов и программы вынесены в Приложение
Целевая функция для всех примеров: f (x1, x2) = c1 x12 +c2 x22 +c12 x1 x2 .
5
1.1. Метод покоординатного спуска (Гаусса – Зейделя)
На каждом шаге метод «приближается» к решению последовательно по каждой из координат. Переход от точки хк к точке хк+1 назовем «внешней» итерацией. Внутри каждой «внешней» итерации находятся n «внутренних» для последовательного вычисления координат точки хк+1:
xk |
=(x1k , x2 k ,....xn k ), |
|
||
k |
′ |
|
′ |
)). |
=( f1 (xk ),.... fn (xk |
||||
|
|
|
′ |
|
x1 ,k +1 = x1k +γk f1 (xk ), |
||||
x2 ,k +1 = x2 k |
+γk |
f2′(x1,k +1 , x2k ,...xnk ), |
||
x3,k +1 = x3k |
+γk |
′ |
+1 , x2,k +1 , x3k ,...xnk ), |
|
f3 (x1,k |
||||
........................................................., |
||||
xn,k +1 = xnk |
+γk |
fn′(x1,k +1 ,....xn−1,k +1 , xn ). |
||
xk +1 =(x1,k +1 ,...xn,k +1 ), |
|
|||
|
′ |
|
′ |
|
k +1 =( f1 (xk +1 ),... fn (xk +1 )
Блок-схема алгоритма метода покоординатного спуска с постоянным шагом (Рис.1П) и программа приведены в Приложении 1. Графическая иллюстрация решения приведена на Рис 1.
1.2. Метод одновременного вычисления координат следующей точки.
1.2.1. Градиентный метод с постоянным шагом.
На каждой итерации метод «приближается» к решению, вычисляя новое значение каждой координаты в соответствии с формулой (3). Блоксхема алгоритма метода с постоянным шагом (Рис.2П) и программа приведены в Приложении. Графическая иллюстрация решения приведена на Рис 2.
1.2.2. Градиентный метод с дроблением шага.
На каждой итерации проверяется, уменьшился ли модуль вектораградиента. Если модуль вектораградиента не уменьшился, величина γ делится, например, пополам, и итерация повторяется заново. Блок-схема алгоритма метода с дроблением шага (Рис.3П) и программа приведены в Приложении. Графическая иллюстрация решения приведена на Рис 3, 4, 5.
6
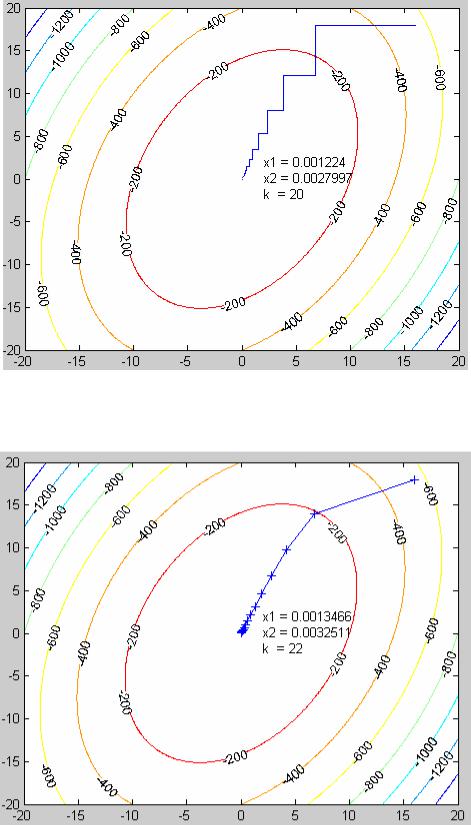
Рис.1. Графическая иллюстрация движения к максимуму методом покоординатного спуска.
Рис.2. Движение к максимуму с постоянным шагом.
7
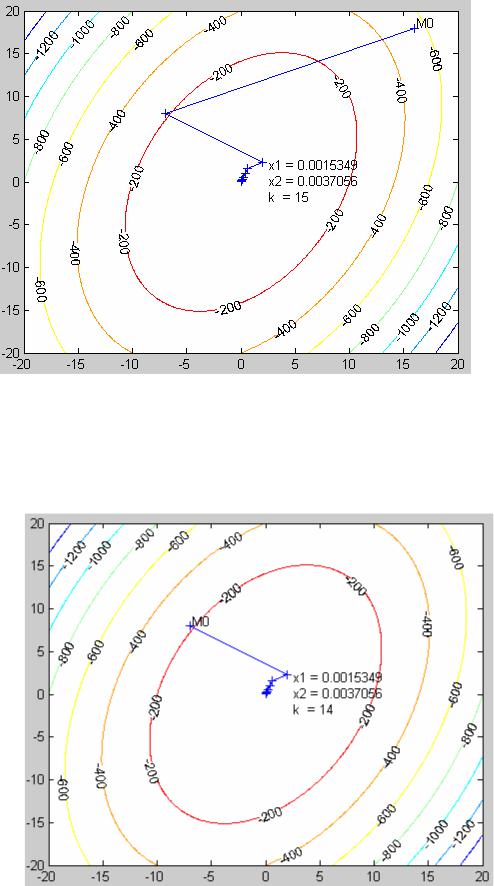
Рис 3. Графическая иллюстрация метода с дроблением шага.
В примере Рис.3 происходит дробление шага на первой итерации алгоритма. В этом можно убедиться, поставив точку останова на строке 56. На Рис.4 и 5 показано движение из разных начальных точек.
Рис.4.
8
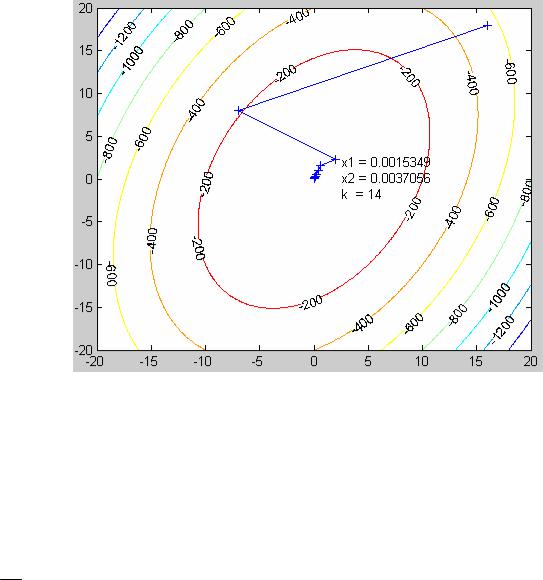
Рис.5.
1.2.3. Градиентный метод наискорейшего спуска.
На каждой итерации вычисляется значение шага γ , максимизирующее
значение целевой функции :
f k +1 = f (x1k +1,K, xnk +1 ) = f (x1k +γk f1′k ,K, xnk +γk fn′k ) =ϕ(γk ) → max
dγϕ = 0 γ .(4)
d k k
Новые координаты вычисляются с помощью этого значения:
xk +1 = xk +γk fn′k (xk )
Скалярное произведение векторов-градиентов на двух смежных итерациях равно нулю:
|
k +1 |
|
|
k +1 |
|
dx |
k +1 |
|
df (x |
|
) |
= |
df (xk +1 |
) |
= f ′(k +1) f ′(k ) = 0 |
(5) |
|
dγk |
|
|
dx |
|
dγk |
|
||
Это означает, что движение от точки к точке происходит по взаимноортогональным направлениям. (Рис.6).
9
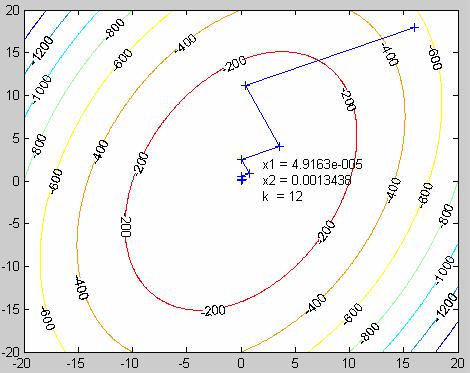
Рис.6. Движение к экстремуму по взаимно-ортогональным направлениям в методе наискорейшего спуска.
Блок-схема алгоритма метода наискорейшего спуска (Рис.4П) и программа приведены в Приложении 1. Графическая иллюстрация решения приведена на Рис 7.
Сравнение методов.
Для сравнения точности и быстродействия методов в данной работе используется следующий простой прием. В вышеприведенных примерах решалась простейшая задача, точное решение которой находится из системы линейных уравнений.
f(x1, x2) = -2*x1^2 - x2^2 + x1*x2 f1′(x) = −4x1 + x2 =0
f2′(x) = −2x2 + x1 =0 x* =0 : x1* =0, x2* =0.
В таблице 1 для каждого метода приводится число итераций к, за которое из одной и той же начальной точки алгоритм приходит в точку хк, норма вектора-градиента в которой становится меньше заданного числа δ =0,01 - точности метода. Точка хк является решением задачи. Методы сравниваются по значению отклонения этой точки от точки х*=0 – точного безусловного максимума .
10
