00 Проектирование цифровых устройств

51

Операция преобразования кода однооперандная. Операнд – двоичное число Qn–1Qn–2…Q1Q0, – хранится в памяти (в n синхронных триггерах). Результат операции – число в дополнительном коде, – записывается в память.

Составим таблицу состояний автомата и функций возбуждения триггеров JK-типа для n = 4.

Необходимо построить 8 диаграмм Вейча для синтеза функций

J3, K3, J2, K2, J1, K1, J0, K0. Для младшего разряда очевидно: J0 = 0;

K0 = 0.

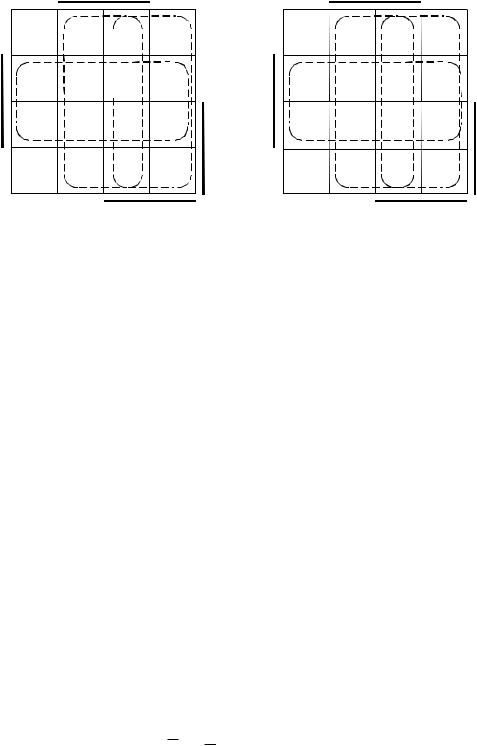
Построим диаграммы для старшего 3-го разряда.

52

Рис. 2.8. Диаграммы Вейча функций J3 и K3

Объединение ячеек, содержащих единицу, дает для обеих функций одинаковые формулы:

J3 K3 Q0 Q1 Q2 .

Выражение Q0 Q1 Q2 является сигналом своеобразного переноса из младших разрядов: p3 Q0 Q1 Q2 . Это справедливо

для всех разрядов:

pi p0 Q0 ... Qi 1 ,

где p0 – входной перенос из младшей группы разрядов. С целью

упрощения аппаратуры можно использовать схему «сквозного» переноса:

pi pi 1 Qi 1 ,

для реализации которой требуются двухвходовые элементы ИЛИ. Если в качестве элементов памяти применяются D-триггеры, то

можно воспользоваться результатами приведенного выше синтеза сигналов переноса, полагая, что при pi = 1 триггер должен инвертировать свое состояние, а при pi = 0 сохранять его неизменным:

Di piQi piQi pi Qi .

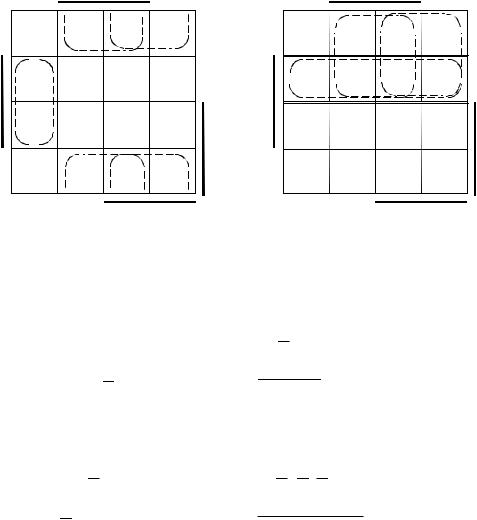
Справедливость этого утверждения подтверждает синтез функции возбуждения Di непосредственно по таблице истинности. Ограничимся старшими разрядами. На рисунке 2.8 изображены диаграммы Вейча функций D2 и D3 для второго и третьего разрядов.

53

Рис. 2.9. Диаграммы Вейча функций D2 и D3

После объединения ячеек, содержащих единицу, получаем выражения функций возбуждения D-триггеров:

D2 Q2 Q0 Q1 Q2Q1Q0

Q2 Q0 Q1 Q2 Q0 Q1

Q0 Q1 Q2 p2 Q2

D3 Q3 Q0 Q1 Q2 Q3Q2Q1Q0

Q3 Q0 Q1 Q2 Q2 Q0 Q1 Q2

Q0 Q1 Q2 Q3 p3 Q3

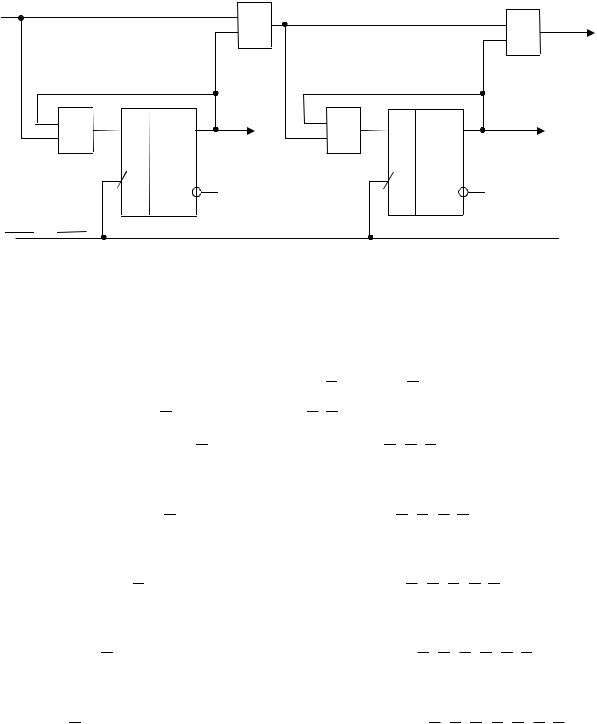
Фрагмент схемы преобразователя двоичного кода в дополнительный код показан на рисунке 2.9. D-триггеры, как правило, управляются фронтом синхросигнала, в данном примере – перепадом сигнала С от нуля к единице. Так как данные на входе D записываются в триггер «на лету», существует опасность временных «состязаний» («гонок») в цепи от выхода триггера до его входа, в результате чего после правильного переключения триггер может успеть переключиться еще раз в соответствии с новым состоянием его выхода. Необходимо проверить временные условия отсутствия гонок:

tтг.min + tКЦmin > th.max,

54

где tтг.min – минимальное время переключения триггера; tКЦmin – минимальная задержка сигнала по пути от выхода триггера до его входа; th.max – максимальное время выдержки триггера.

C

Рис.2.10. Схема реализации операции преобразования кода

Анализируя структуру выражений для функций возбуждения D- триггеров, можно по аналогии написать формулы при большем числе триггеров. Например, если n = 8, то

D0 Q0 0 Q0; D1 Q1Q0 Q1Q0 Q0 Q1;

D2 Q2 Q0 Q1 Q2Q1Q0 Q0 Q1 Q2 ;

D3 Q3 Q0 Q1 Q2 Q3Q2Q1Q0

Q0 Q1 Q2 Q3;

D4 Q4 Q0 Q1 Q2 Q3 Q4Q3Q2Q1Q0

Q0 Q1 Q2 Q3 Q4 ;

D5 Q5 Q0 Q1 Q2 Q3 Q4 Q5Q4Q3Q2Q1Q0

Q0 Q1 Q2 Q3 Q4 Q5;

D6 Q6 Q0 Q1 Q2 Q3 Q4 Q5 Q6Q5Q4Q3Q2Q1Q0

Q0 Q1 Q2 Q3 Q4 Q5 Q6;

D7 Q7 Q0 Q1 Q2 Q3 Q4 Q5 Q6 Q7Q6Q5Q4Q3Q2Q1Q0

Q0 Q1 Q2 Q3 Q4 Q5 Q6 Q7.

55

2.3.Счетчики импульсов

2.3.1.Двоичные и двоично-кодированные счетчики

Специфичной для счетчиков является микрооперация инкремента или декремента, то есть изменение содержимого на единицу. Состояние счетчика выражается двоичным кодом, считываемым с выходов триггеров, например, для четырехразрядного счетчика – кодом Q3Q2Q1Q0. Счетчик характеризуется, прежде всего, модулем счета (емкостью) M, равным количеству различных состояний, составляющих цикл работы.

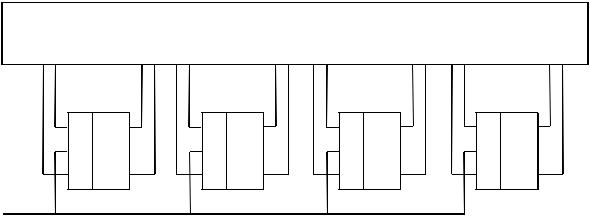
В параллельных счетчиках переключение триггеров во всех разрядах осуществляется синхронно по счетному импульсу, при этом новое состояние триггера в каждом разряде определяется сигналами на его информационных входах, которые вырабатываются в комбинационной схеме.

Комбинационная цепь

Рис.2.11. Схема 4-разрядного счетчика на JK-триггерах

На рисунке 2.10 в качестве примера приведена структурная схема синхронного счетчика на JK-триггерах. Сигналы с выходов триггеров поступают в комбинационную схему, которая преобразует их в сигналы возбуждения триггеров. Указанные сигналы подаются на информационные входы Ji и Ki (i = 0, …, 3) триггеров и подготавливают их для переключения счетчика в требуемое состояние. Переключение триггеров происходит по счетному импульсу, поступающему на синхровходы триггеров.

Функции возбуждения каждого, i-го, триггера определяются “старым” состоянием счетчика Q3Q2Q1Q0 (до переключения), и их вид зависит от алгоритма счета и от типа применяемых триггеров.

56

Таким образом, если задан тип триггера, то задача логического проектирования схемы счетчика заключается в составлении функций возбуждения каждого триггера и минимизации найденных функций в заданном базисе.

Двоичные счетчики. Модуль n-разрядного двоичного счетчика соответствует целой степени двойки (M = 2n). По направлению счета различают суммирующие (Up–counter), вычитающие (Down–counter) и реверсивные (Up–down–counter) счетчики.

Структуру двоичного счетчика можно получить эвристическим путем (внимательно рассмотрев особенности последовательности двоичных чисел) или с применением формального синтеза.

Рассмотрим случай суммирующего счетчика. В процессе прибавления единицы к двоичному числу, например,

результат отличается от исходного числа только в младших разрядах до первого нулевого включительно. Изменение заключается в инвертировании состояний. В этом и состоит функция счетчика.

Для переключения триггера в i-м разряде ему необходимо обеспечить режим Т–триггера при наличии сигнала переноса pi, который должен возникать, если триггеры во всех младших разрядах были в единичном состоянии, т. е.

pi Qi 1Qi 2...Q1Q0 .

В случае вычитающего счетчика результат отличается от исходного числа во всех младших разрядах до первого единичного включительно. Следовательно, для переключения триггера в i-м разряде ему необходимо обеспечить режим Т–триггера при наличии сигнала заема zi, который должен возникать, если триггеры во всех младших разрядах были в нулевом состоянии, т. е.

zi Qi 1Qi 2...Q1Q0 .

Сигнал переноса (или заема) используется для формирования функций возбуждения триггера в соответствии с таблицей переходов применяемых триггеров.

57

Из формул для переноса (заема) видно, что эти сигналы во всех разрядах счетчика вырабатываются одновременно с помощью многовходовых конъюнкторов. В счетчиках со сквозным переносом сигнал переноса (заема) распространяется по цепочке двухвходовых конъюнкторов:

pi pi 1Qi 1 или zi zi 1Qi 1 .

Сигнал переноса распространяется до ближайшего разряда, содержащего нуль, а сигнал заема – до ближайшего разряда, содержащего единицу.

2.3.2. Счетчики импульсов в коде Грея

Код, связанным с именем Ф. Грея, который применил его для построения преобразователя угловых перемещений в цифровой код, обладающий явными преимуществами перед преобразователем с двоичным кодом. Код Грея относится к таким, в которых при переходе от любой кодовой комбинации к следующей изменяется только один разряд. В схемотехнике счетчиков это свойство устраняет одновременное переключение многих разрядов, характерное для двоичных счетчиков при некоторых переходах. Одновременное переключение многих элементов создает такие токовые импульсы в цепях питания схем, которые могут вызывать сбои в работе схемы. В ряде БИС/СБИС применение двоичных счетчиков большой разрядности не разрешается, и они заменяются счетчиками с кодом Грея и последующим преобразованием кода Грея в двоичный. Сложность счетчика с кодом Грея ненамного больше, чем сложность двоичного счетчика, преобразователь кодов также относительно прост.

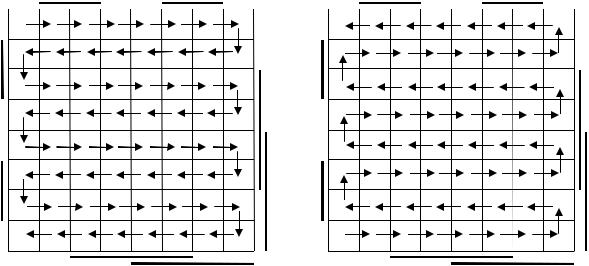
Счетчик с кодом Грея можно построить формальным способом, исходя из таблицы переходов счетчика. На рисунке 2.11,а показана «траектория» кодов состояния счетчика в режиме прямого счета (инкремента), а на рисунке 2.11,б – в режиме обратного счета (декремента). Каждое новое состояние счетчика соответствует переходу из одной ячейки карты Карно (диаграммы Вейча) в соседнюю.

58

Суммирующие счетчики с кодом Грея. Наибольшее применение в схемах счетчиков находят триггеры JK- и D-типа. При синтезе функций возбуждения JK-триггеров выражения для Ji и Ki получаются более простыми, чем для D-триггеров, зато в последнем случае сигналов управления триггерами вдвое меньше.

Рассмотрим вначале пример синтеза функций возбуждения триггеров Ji и Ki суммирующего счетчика на JK-триггерах. Ограничимся случаем 6-разрядного счетчика, так как диаграммы Вейча для большего числа переменных становятся громоздкими. Анализируя полученные выражения для Ji и Ki, можно «предугадать» формулы и для счетчиков с количеством разрядов больше 6. Приводя выражения для функций возбуждения к окончательному виду, следует обратить внимание на возможность применения логического элемента типа ИСКЛЮЧАЮЩЕЕ ИЛИ, который позволяет существенно упростить формулы. Элементы XOR (сложение двух переменных по модулю 2) имеются в большинстве серий интегральных микросхем.

Следуя траектории перемещения кода состояний (см. рис. Х.хх, а), отмечаем в ячейках карты Карно (диаграммы Вейча) необходимые значения переменных Ji или Ki. Ниже показан пример

59

синтеза функций возбуждения JK-триггера. В 6-разрядном счетчике

этих функций 12: J0, K0, J1, K1, J2, K2, J3, K3, J4, K4, J5, K5.

Получив после «склеивания» соседних ячеек минимизированные выражения для переменных Ji и Ki в младших разрядах, необходимо обнаружить общие свойства структуры этих формул и, следуя принципу индукции, найти выражения для указанных функций в многоразрядных (например, 8-разрядных) счетчиках.

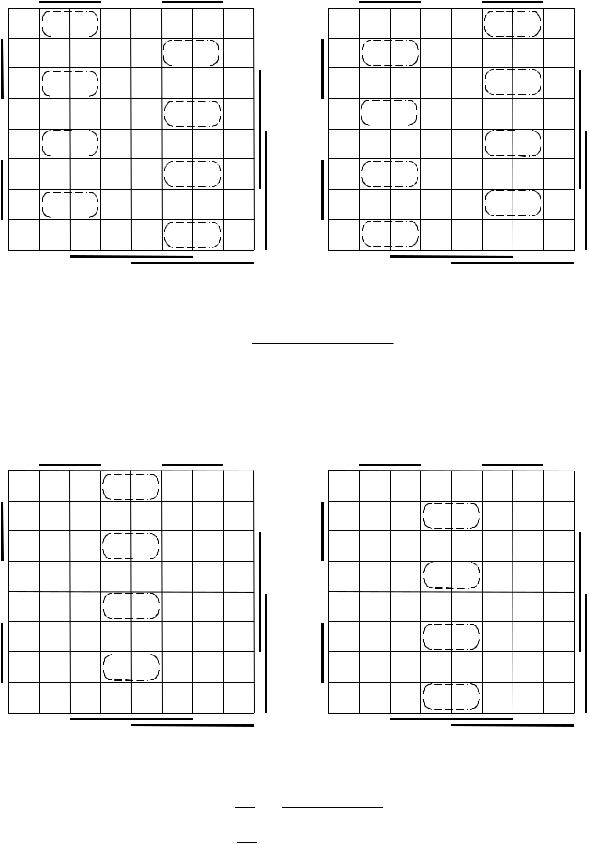
Рис. 2.13. Диаграммы Вейча для младшего разряда суммирующего счетчика

J0 Q1 Q2 Q3 Q4 Q5

K0 Q1 Q2 Q3 Q4 Q5

60

Рис. 2.14. Диаграммы Вейча для первого разряда суммирующего счетчика

J1 Q0 Q2 Q3 Q4 Q5

K1 Q0 Q2 Q3 Q4 Q5

Рис. 2.15. Диаграммы Вейча для второго разряда суммирующего счетчика

J2 Q0Q1 Q3 Q4 Q5

K2 Q0Q1 Q3 Q4 Q5