
билет 2
.pdf
потери общности можно принять |
, тогда |
Тогда подставив в |
передаточную характеристику дискретного фильтра (4) |
, мы получим |
|
передаточную характеристику фильтра по Лапласу, из которой можно получить
комплексный |
коэффициент |
передачи |
дискретного |
фильтра |
путем |
подстановки |
. Таким |
образом, комплексный коэффициент |
передачи |
||
цифрового фильтра обозначается как  и равен:
и равен:
(5
)
Амплитудно-частотная характеристика (АЧХ) цифрового фильтра может быть получена как модуль 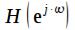 , а фазочастотная (ФЧХ) как аргумент:
, а фазочастотная (ФЧХ) как аргумент:
(6)
Также вводят понятие групповой задержки как производной от ФЧХ:
(7)
Обратите внимание, что АЧХ и ФЧХ и групповая задержка цифрового фильтра есть непрерывные функции частоты. При этом согласно (5) 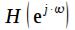
периодическая функция с периодом 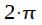 , так как
, так как 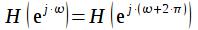 . Последнее равенство не вызывает сомнений, если подставить его в выражение (5). Таким образом, характеристику цифрового фильтра достаточно проанализировать
. Последнее равенство не вызывает сомнений, если подставить его в выражение (5). Таким образом, характеристику цифрового фильтра достаточно проанализировать
на интервале 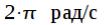 .
.
Цифровой фильтр также определяется своей импульсной характеристикой, преобразование Фурье от которой дает комплексный коэффициент передачи. Если комплексный коэффициент передачи — периодическая функция частоты, то
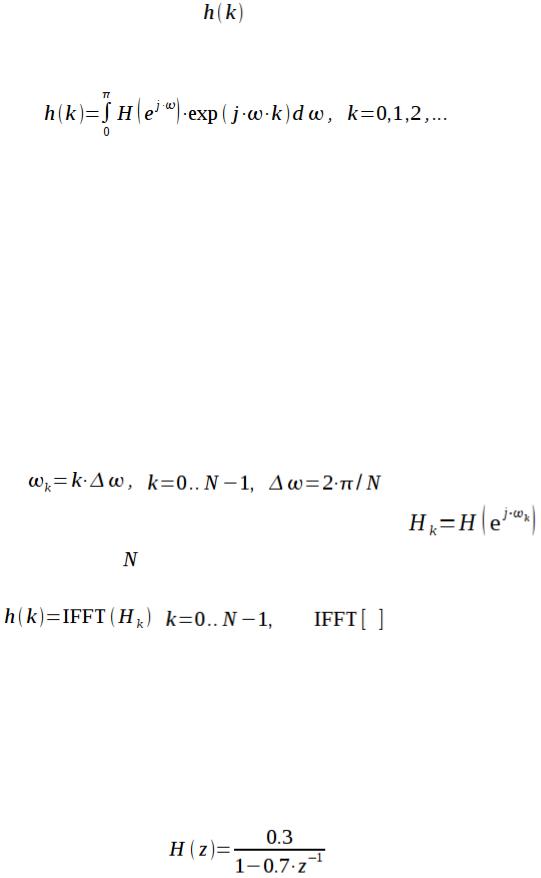
импульсная характеристика |
дискретного фильтра определяется как |
разложение в ряд Фурье  :
:
(8)
.
Рассчитывать импульсную характеристику через интеграл не совсем удобно,
кроме того количество отсчетов импульсной характеристики 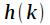 БИХ-фильтра бесконечно, и все их рассчитать невозможно. Однако, если фильтр устойчивый, то
БИХ-фильтра бесконечно, и все их рассчитать невозможно. Однако, если фильтр устойчивый, то
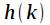 убывает, с увеличением
убывает, с увеличением 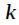 , и можно рассчитать заданное количество отсчетов импульсной характеристики фильтра при помощи быстрого преобразования Фурье (FFT).
, и можно рассчитать заданное количество отсчетов импульсной характеристики фильтра при помощи быстрого преобразования Фурье (FFT).
Пусть требуется рассчитать 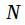 первых отсчетов импульсной характеристики фильтра, заданного передаточной характеристикой
первых отсчетов импульсной характеристики фильтра, заданного передаточной характеристикой 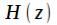
Первое, что мы должны сделать — рассчитать комплексный коэффициент передачи заданного фильтра. Для численного расчета необходимо задать сетку
частот |
|
|
|
. Тогда на данной сетке |
|
частот рассчитаем комплексный коэффициент передачи |
, таким |
||||
образом, |
получим |
отсчетов комплексного коэффициента передачи фильтра. |
|||
После |
этого |
можно |
рассчитать |
импульсную |
характеристику |
как |
|
, |
где |
- оператор обратного |
|
быстрого преобразования Фурье. Таким образом, мы рассчитали характеристики фильтра с заданной передаточной характеристикой. Данный путь расчета приводил к комплексному коэффициенту передачи в частотной области, с последующим преобразованием во временную.
На рисунках 6 и 7 показаны рассчитанные характеристики фильтра при 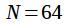 и
и
(9)
.
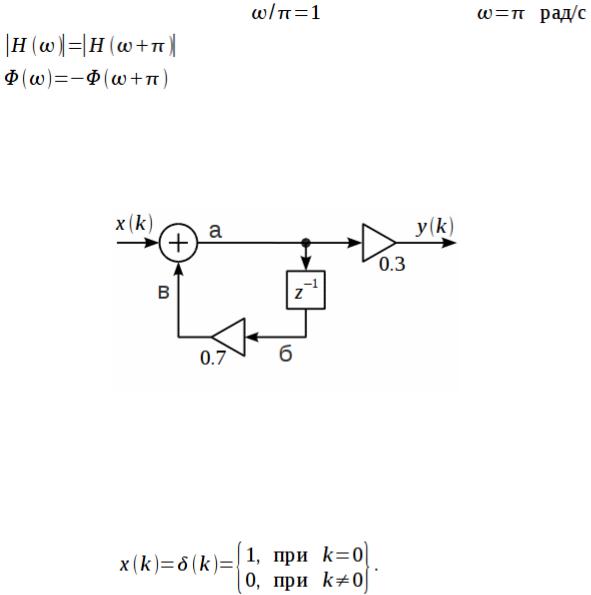
Рисунок 6: Импульсная характеристика |
Рисунок 7: Один период АЧХ и ФЧХ фильтра |
фильтра |
|
Обратите внимание, что на рисунке 7 по оси абсцисс показана частота  , таким образом, АЧХ и ФЧХ представлена для нормированных частот от 0 до 2.
, таким образом, АЧХ и ФЧХ представлена для нормированных частот от 0 до 2.
Кроме того, можно заметить, что АЧХ фильтра 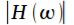 является симметричной
является симметричной
относительно |
частоты |
|
, |
или |
, |
|
т.е. |
, |
а |
ФЧХ |
является |
антисимметричной, |
|
т.е. |
. |
|
|
|
|
|
Структурную схему фильтра, заданного передаточной характеристикой (9) (рисунок 8).
Рисунок 8: Структурная схема фильтра
Для того, чтобы получить импульсную характеристику цифрового фильтра,
необходимо подать на вход сигнал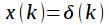 :
:
(10)
Тогда на выходе фильтра будет импульсная характеристика. Рассчитаем импульсную характеристику на выходе фильтра по его структуре.
Выводы

Таким образом, мы привели структурные схемы цифровых КИХ и БИХ фильтров и привели их характеристики. Была представлена структура КИХ фильтра, а также прямая и каноническая формы БИХ фильтров. Рассмотрены характеристики цифровых фильтров: комплексный коэффициент передачи, АЧХ, ФЧХ, групповая задержка и импульсная характеристика фильтра. Приведены способы численного расчета характеристик фильтра по его передаточной функции в частотной и во временной областях.
Характеристика цифровых фильтров
Линейный стационарный цифровой фильтр характеризуется передаточной функцией. Передаточная функция может описать, как фильтр будет реагировать на входной сигнал. Таким образом, проектирование фильтра состоит из постановки задачи (например, фильтр восьмого порядка, фильтр нижних частот с конкретной частотой среза), а затем производится расчет передаточной функции, которая определяет характеристики фильтра
.
Передаточная функция фильтра имеет вид:
где порядок фильтра - большее N или M. В данном случае это формула БИХ-фильтра. Если знаменатель равен единице, то получаем формулу КИХ-фильтра (без обратной связи).
Импульсной характеристикой называют реакцию фильтра на единичный импульс поданный на его вход. Под единичным импульсом понимается такой сигнал, что в момент времени t=0 он равен 1, а во все остальные моменты времени он равен нулю.
Если взглянуть на формулу реализующую цифровой фильтр и подставить туда единичный импульс для последовательных моментов времени, то мы увидим, что для КИХфильтров импульсная характеристика совпадает с набором коэффициентов В, и показывает веса для элементов входного временного ряда.
Любой временной ряд заданный в дискретном виде можно представить как сумму единичных импульсов в разные (последовательные) моменты времени взятых с амплитудой соответствующей значению сигнала в этот момент времени. Для линейных цифровых фильтров откликом на входной сигнал будет просто сумма откликов на каждый входящий в сигнал единичный импульс.
Импульсная характеристика - это очень важная характеристика цифрового фильтра. Она полностью и однозначно описывает его свойства. Т.е. нет никаких дополнительных характеристик линейного ЦФ, которые было бы невозможно получить из импульсной характеристики.
Сама по себе Импульсная характеристика может быть не очень удобна для изучения свойств ЦФ, поэтому вместо нее обычно используют производные от нее
Амплитудно-частотную (АЧХ) и Фазочастотную характеристики (ФЧХ).
Они связаны с импульсной характеристикой преобразованием Фурье. Эта связь опять же взаимно однозначна, т.е. из АЧХ и ФЧХ можно восстановить импульсную характеристику.

|
|
|
|
Характеристики цифровых фильтров |
|
|
|
цифровой фильтр задается свой передаточной характеристикой |
, которая |
||
представляет отношение z-образов |
выходного сигнала ко входному |
: |
|
|
|
|
|
(4
)
z-преобразование мы получили путем отображения комплексной s-плоскости вида  где
где 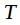 - период дискретизации исходного сигнала и импульсной характеристики фильтра. Без потери общности можно принять
- период дискретизации исходного сигнала и импульсной характеристики фильтра. Без потери общности можно принять 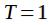 ,
,
тогда 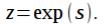 Тогда подставив в передаточную характеристику дискретного
Тогда подставив в передаточную характеристику дискретного
фильтра (4) 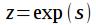 , мы получим передаточную характеристику фильтра по Лапласу, из которой можно получить комплексный коэффициент передачи дискретного
, мы получим передаточную характеристику фильтра по Лапласу, из которой можно получить комплексный коэффициент передачи дискретного
фильтра путем подстановки 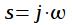 . Таким образом, комплексный коэффициент передачи цифрового фильтра обозначается как
. Таким образом, комплексный коэффициент передачи цифрового фильтра обозначается как 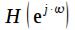 и равен:
и равен:
(5
)
Амплитудно-частотная характеристика (АЧХ) цифрового фильтра может быть получена как модуль 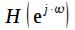 , а фазочастотная (ФЧХ) как аргумент:
, а фазочастотная (ФЧХ) как аргумент:
(6)
Также вводят понятие групповой задержки как производной от ФЧХ:

Виды цифровых фильтров
КИХ-фильтры. Фильтр с конечной импульсной характеристикой (нерекурсивный фильтр, КИХ-фильтр) — один из видов электронных фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какогото момента времени она становится точно равной нулю). Знаменатель передаточной функции такого фильтра — некая константа.
БИХ-фильтры. Фильтр с бесконечной импульсной характеристикой (рекурсивный фильтр, БИХ-фильтр) — электронный фильтр, использующий один или более своих выходов в качестве входа, то есть образует обратную связь.Основным свойством таких фильтров является то, что их импульсная переходная характеристика имеет бесконечную длину во временной области, а передаточная функция имеет дробно-рациональный вид. Такие фильтры могут быть как аналоговыми так и цифровыми.
Выбор между КИХ- и БИХ-фильтрами зависит от относительных преимуществ обоих типов. Сравнительные характеристики фильтров обоих типов представлены в таблице:
КИХ Фильтры |
БИХ фильтры |
|
|
|
|
КИХ-фильтры могут иметь строго линейную |
|
|
фазовую характеристику. Следовательно, фильтр |
|
|
не вводит фазового искажения в сигнал, что важно |
Фазовая характеристика БИХ-фильтров |
|
во многих сферах, например, передаче данных, |
нелинейна, особенно на краях полос. |
|
биомедицине, цифровой аудио обработке или |
|
|
обработке изображений. |
|
|
|
|
|
КИХ-фильтры реализованы нерекурсивно, т.е. |
Гарантировать устойчивость БИХ- |
|
(что следует непосредственно из формулы (6.2)) |
||
фильтров удается не всегда. |
||
они всегда устойчивы. |
||
|
||
|
|
Для реализации фильтров используется ограниченное число битов. Практические последствия этого явления: шум округления и ошибки квантования
менее существенны для КИХ-фильтров |
более существенны для БИХ-фильтров |
|
|
Чтобы получить конечную импульсную характеристику с помощью фильтров с резкими срезами характеристики, потребуется больше коэффициентов, чем для получения бесконечной импульсной характеристики.
Следовательно, для реализации предложенной |
Следовательно, для реализации пред- |
спецификации амплитудной характеристики с |
ложенной спецификации амплитудной |
КИХ необходимо больше вычислительной |
характеристики с БИХ необходимо меньше |
|
|
мощности и памяти. |
вычислительной мощности и памяти |
|
Эффективность КИХ-реализаций можно |
|
|
значительно повысить, сыграв на вычислительной |
|
|
скорости БПФ и обработке при нескольких |
|
|
скоростях |
|
|
|
|
|
Для получения КИХ-фильтров такое |
Аналоговые фильтры легко |
|
преобразование невозможно, поскольку для них не |
||
преобразовать в эквивалентные цифровые |
||
существует аналоговых прототипов. Впрочем, |
||
БИХ-фильтры, удовлетворяющие сходным |
||
получать произвольные частотные характеристики |
||
спецификациям. |
||
на КИХ-фильтрах легче. |
||
|
||
|
|
|
Получать произвольные частотные |
Получать произвольные частотные |
|
характеристики на КИХ-фильтрах легче. |
характеристики на БИХ-фильтрах сложнее. |
|
|
|
|
Синтез КИХ-фильтров алгебраически сложнее, |
|
|
если не использовать компьютерную поддержку |
Синтез БИХ-фильтров осуществляется |
|
|
||
разработки. |
более простыми способами. |
|
|
||
|
|
|
КИХ фильтры не рекуррентны. Это означает, |
БИХ-фильтры рекуррентны. Это |
|
что, пропустив через фильтр один и тот же сигнал, |
означает, что, пропустив через фильтр один |
|
но с "обратным ходом времени", мы получим |
и тот же сигнал, но с "обратным ходом |
|
одинаковые результаты. (верно в случае |
времени", мы получим, вообще говоря, |
|
симметричности коэффициентов) |
разные результаты. |
|
|
|
Вопрос 5
Разработка технического задания
Раньше регламентировалось ГОСТ 34.602.89 ТЗ состоит из след. разделов:
1.введение
2.хар-ка объекта
3.назначение сис-мы
4.основные треб-ия к оборуд-ию
5.технико-эк. показатели
6.порядок приемки-сдачи Задание на сис. анализ содержит формулировку целей и проблем исслед-ия, уточнение
ресурсов исслед-ия, принцип выделения сис-мы из окружающей среды. Далее опред-ся ограничения и возможные альтернативы, соглас-ие целей подсис-м, анализ и оценка сис. ф-ий, принципы проведения испытаний.
Подавление шумов
Усреднение изображений часто используется в высококлассной астрофотографии, но, вероятно, недоиспользуется в других типах съёмки при малом свете или ночью.
Усреднение способно подавить шумы, не разрушив детальность, поскольку оно по сути увеличивает соотношение сигнал-шум (SNR) изображения. Дополнительным выигрышем является то, что усреднение может заодно повысить глубину цветности изображения — за грань возможностей одиночного снимка
Линейное усреднение пикселей
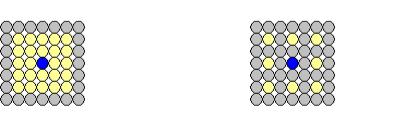
Простейшая идея удаления шума - усреднять значения пикселей в пространственной окрестности. Для каждого пикселя анализируются соседние для него пиксели, которые располагаются в некотором прямоугольном окне вокруг этого пикселя (см. рисунок 2.1.1а). Чем больше взят размер окна, тем сильнее происходит усреднение. Самый простой вариант фильтрации - в качестве нового значения центрального пиксела брать среднее арифметическое всех тех его соседей, значение которых отличается от значения центрального не более чем на некоторый порог. Чем больше величина этого порога, тем сильнее происходит усреднение.
Вместо среднего арифметического соседей можно брать их взвешенную сумму, где весовой коэффициент каждого соседнего пиксела зависит либо от расстояния в пикселях от него до центрально пикселя, либо от разницы их значений.
Эти алгоритмы очень простые, но они не дают хорошего результата.
Интересная модификация этого метода была предложена Де Хааном [4-6]. Он предложил в качестве значения центрального пикселя также брать взвешенную сумму соседних пикселей, только соседей брать не подряд, а через один или два пикселя (см. рисунок 2.1.1б). Утверждается, что при таком подходе удается подавить низкочастотный шум, который заметнее на глаз, чем высокочастотный.
|
|
Рисунок 2.1.1а. |
Рисунок 2.1.1б. |
Обычный вид окна |
Вид окна в алгоритме Де Хаана |
|
|
Аналогично можно применять этот метод во временной области, только усреднение будет производиться уже между соседними кадрами, и окно соответственно будет браться по времени (то есть каждый пиксель будет усредняться по пикселям, расположенным в той же позиции в соседних кадрах). В общем виде такую схему шумоподавления можно выразить следующей формулой:

,
где x - пиксель, а t - номер кадра. Веса  могут браться в зависимости от близости значений пикселей и расстояния между кадрами. Также усреднение может проводиться рекурсивно:
могут браться в зависимости от близости значений пикселей и расстояния между кадрами. Также усреднение может проводиться рекурсивно:
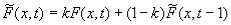 ,
,
где  - значение, посчитанное для этого пиксела в предыдущем кадре. Для предотвращения возникновения ореолов вокруг движущихся объектов, о которых было сказано выше, во временные фильтры встраивают алгоритмы определения движения. При этом возможно два варианта: простое детектирование движения (пикселы в движущихся блоках просто остаются без изменения, и шум вдоль движущихся объектов не подавляется) или построение скомпенсированного предыдущего и/или следующего кадра (см. [27]) и смешивание текущего с ним. В последнем случае компенсация движения должна быть выполнено качественно, иначе будут артефакты на месте неправильно найденных блоков.
- значение, посчитанное для этого пиксела в предыдущем кадре. Для предотвращения возникновения ореолов вокруг движущихся объектов, о которых было сказано выше, во временные фильтры встраивают алгоритмы определения движения. При этом возможно два варианта: простое детектирование движения (пикселы в движущихся блоках просто остаются без изменения, и шум вдоль движущихся объектов не подавляется) или построение скомпенсированного предыдущего и/или следующего кадра (см. [27]) и смешивание текущего с ним. В последнем случае компенсация движения должна быть выполнено качественно, иначе будут артефакты на месте неправильно найденных блоков.
Визуальный шум может ухудшить степень детальности цифровых или плёночных фотографий, поэтому подавление этого шума может значительно улучшить итоговое изображение или отпечаток. Большинство методов шумоподавления всегда заодно размывает изображение. Некоторое сглаживание может быть приемлемо для изображений, на которых господствует вода или небо, но листва в пейзажах может пострадать даже от наиболее осторожных попыток подавления шума.
Концепция
Усреднение изображений работает на основе предположения об абсолютно случайной природе шума в изображении. Соответственно, случайные отклонения от истинных данных в изображении будут последовательно снижаться по мере усреднения возрастающего числа изображений. Для 2 ух изобрапжений
Вышеприведенный график отражает флюктуации яркости в верхнем и нижнем изображениях синей и красной линиями, соответственно. Горизонтальная черта отражает среднее значение, которое соответствует идеальному виду изображения с нулевым уровнем шума. Колебания красной и синей линий уникальны и независимы. Если мы усредним значения пикселей в каждой из точек графика, мы получим снижение вариативности яркости, как показано ниже:
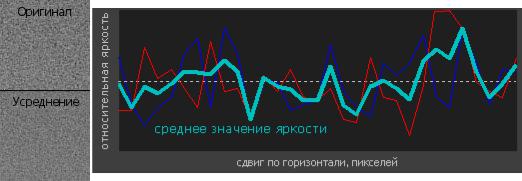
Несмотря на то, что результат усреднения двух графиков продолжает колебаться относительно идеального среднего, его максимальное отклонение значительно уменьшилось. Визуально это приводит к тому, что образец выглядит более гладко. Усреднение двух изображений обычно даёт уровень шума, соответствующий половинной чувствительности ISO, так что два изображения, снятые при ISO 400, будут сравнимы с одним, снятым при ISO 200, и так далее. Уровень шума падает на квадратный корень от числа усреднённых изображений, то есть для снижения уровня шума вдвое требуется усреднить 4 изображения.
Усреднение изображений с использованием слоёв
Adobe Photoshop позволяет относительно быстро усреднить изображения, используя слои. Идея в том, чтобы положить каждое из изображений в отдельный слой и наложить их так, чтобы каждое изображение вносило равный вклад. Если по какой-то причине один из слоёв получает больший вес, чем прочие, эффективность усреднения понизится.
Следует сперва загрузить все усредняемые изображения в Photoshop и затем расположить их в слоях одно над другим в одном проекте. GIMP позволяет открывать изображения непосредственно как слои. После того как все усредняемые изображения оказались в слоях одного проекта, можно приступать собственно к усреднению.
При усреднении следует помнить, что плотность каждого слоя определяет, насколько будет виден слой, лежащий под ним, и то же самое справедливо для всех последующих слоёв. Это означает, что для корректного усреднения четырёх изображений недостаточно будет поставить плотность каждого слоя равной 25%. Вместо этого для нижнего (фонового) слоя нужно задать плотность 100%, для следующего над ним слоя 50%, для слоя над ним 33% и, наконец, для самого верхнего слоя 25%. Это проиллюстрировано ниже:
