2. Основы молекулярной физики и термодинамики

2.1. Основные понятия молекулярной физики и термодинамики

Молекулярная физика - раздел физики, в котором изучаются физические свойства и строение вещества в различных агрегатных состояниях на основе их микроскопического (молекулярного) строения.

Молекулярно-кинетическая теория строения вещества - раздел молекулярной физики, в котором изучаются свойства тел на основе представлений об их молекулярном строении.

Статистическая физика – раздел молекулярной физики, в котором изучаются свойства и движения не отдельных молекул (частиц), а совокупности частиц, характеризующиеся средними величинами.

Термодинамика – наука, в которой изучаются свойства физических систем вне связи с их микроскопическим строением.

Система – совокупность рассматриваемых тел (в частности: молекул, атомов, частиц).

Параметры состояния системы: p-давление, V- объём, T-температура.

а) Интенсивные параметры - параметры (давление, температура, концентрация и др.), не зависящие от массы системы.

Температура - физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Свойство температуры - определять направление теплового обмена. Температура в молекулярной физике определяет распределение частиц по уровням энергии и распределение частиц по скоростям.

Термодинамическая температурная шкала - температурная шкала, определяемая температура (абсолютная температура) в которой всегда положительна.

б) Экстенсивные параметры - параметры (объем, внутренняя энергия, энтропия и др.), значения которых пропорциональны массе термодинамической системы или ее объему.

Внутренняя энергия системы - суммарная кинетическая энергия хаотического движения молекул, потенциальная энергия их взаимодействия и внутримолекулярная энергия, т.е. энергия системы без учёта кинетической энергии её в целом (при движении) и потенциальной энергии во внешнем поле.

Изменение внутренней энергии при переходе системы из состояния в состояние равно разности значений внутренней энергии в этих состояниях и не зависит от пути перехода системы из одного состояния в другое.

Уравнение состояния системы:

F(p,V,T) = 0. (2.1)

Неравновесное состояние системы – такое, при котором какой-либо из ее параметров состояния системы изменяется.

Равновесное состояние системы - такое, при котором все параметры состояния системы имеют определённые значения, постоянные при неизменных внешних условиях.

Время релаксации - время, в течение которого система приходит в равновесное состояние.

Процесс – переход системы из одного состояния в другое состояние, связанный с изменением хотя бы одного из ее параметров состояния:

а) обратимый процесс - процесс, при котором возможно осуществить обратный переход системы из конечного в начальное состояние через те же промежуточные состояния так, чтобы не осталось никаких изменений в окружающей систему среде;

б) необратимый процесс - процесс, при котором невозможно осуществить обратный переход системы в первоначальное состояние, или если по окончании процесса в окружающей среде или в самой системе произошли какие-либо изменения;

в) круговой процесс (цикл) - такая последовательность превращений, в результате которой система, выйдя из какого-либо исходного состояния, возвращается в него вновь. Любой круговой процесс состоит из процессов расширения и сжатия. Процесс расширения сопровождается работой, совершаемой системой, а процесс сжатия - работой, совершаемой над системой внешними силами. Разность этих работ равна работе данного цикла.

Динамические закономерности - закономерности, подчиняющиеся системам уравнений (в том числе дифференциальных, интегральных и др.), допускающих существование единственного решения для каждого начального условия.

Статистические закономерности - количественные закономерности, устанавливаемые статистическим методом, в котором рассматриваются лишь средние значения величин, характеризующих данную совокупность молекул (рассматривается конкретная молекулярная модель, и к ней применяются математические методы статистики, основанные на теории вероятностей).

Вероятность термодинамическая - число способов, которыми может быть реализовано данное состояние макроскопической физической системы (предел, к которому стремится относительная частота появления некоторого события при достаточно большом, стремящемся к бесконечности числе повторений опыта при неизменных внешних условиях):

w = n/N, (2.2)

где N - число опытов;

n - число раз получено определенное событие.

Флуктуации - случайные отклонения физических величин от их среднего значения.

Молекула - наименьшая часть вещества, обладающая его основными химическими свойствами и состоящая из атомов, соединенных между собой химическими связями.

Атом - часть вещества микроскопических размеров (микрочастица), наименьшая частица химического элемента, обладающая его свойствами. Атомы в разных сочетаниях входят в состав молекул разных веществ.

Относительная атомная масса - отношение массы данного атома к 1/12 массы изотопа углерода с массовым числом 12 (¹²С).

Относительная молекулярная масса - отношение массы данной молекулы к 1/12 массы атома ¹²С.

Моль - количество вещества, в котором содержится число частиц (атомов, молекул и других частиц), равное числу атомов в 0,012 кг изотопа углерода С¹².

Число Авогадро - число атомов или молекул в моле любого вещества: N_А = 6,0210²³ моль^-1.

Молярная масса - масса вещества, взятого в количестве одного моля:

 = m₀N_А. (2.3)

2.2. Основные представления и законы молекулярно-кинетической теории

Идеальный газ - теоретическая модель газа, в которой не учитывается взаимодействие его частиц (средняя кинетическая энергия частиц много больше энергии их взаимодействия). Размеры молекул идеального газа малы по сравнению с расстояниями между ними. Суммарный собственный объем молекул такого газа мал по сравнению с объемом сосуда. Силы взаимодействия между молекулами настолько малы, что движение молекул от столкновения до столкновения происходит по прямолинейным отрезкам. Число ежесекундных столкновений молекул велико.

Основные положения молекулярно-кинетической теории идеального газа:

1) газ состоит из мельчайших частиц - атомов или молекул, находящихся в непрерывном движении;

2) в любом, даже очень малом объёме, к которому применимы выводы молекулярно-кинетической теории, число молекул очень велико;

3) размеры молекул малы по сравнению с расстояниями между ними;

4) молекулы газа свободно движутся между двумя последовательными взаимодействиями друг с другом или со стенками сосуда, в котором он находится. Силы взаимодействия между молекулами, кроме моментов соударения, пренебрежимо малы. Соударения молекул происходят без потерь механической энергии, т.е. по закону абсолютно упругого взаимодействия;

5) при отсутствии внешних сил молекулы газа распределяются равномерно по всему объёму;

6) направления и значения скоростей молекул газа самые различные.

Основное уравнение молекулярно-кинетической теории газов:

, (2.4)

где - средняя квадратичная скорость.

Основное уравнение молекулярно-кинетической теории газов для давления:

, , (2.5)

где n₀ = N^'/V - число молекул в единице объема;

- средняя кинетическая энергия поступательного движения молекул газа;

k - постоянная Больцмана.

Закон Авогадро: в одинаковых объемах при одинаковых температурах и давлениях содержатся одинаковые количества молекул.

Закон Дальтона: давление смеси газов равно сумме парциальных давлений, т.е. тех давлений, которые имел бы каждый из входящих в смесь газов, если бы в объеме, занятом смесью, находился он один:

. (2.6)

Уравнение состояния идеальных газов для произвольной массы m (уравнение Менделева-Клапейрона):

, (2.7)

где R - газовая постоянная, которая численно равна работе расширения одного моля газа при его нагревании на один градус в условиях постоянного давления;

T - абсолютная температура.

Степени свободы i - число независимых координат, необходимых для полного описания положения системы в пространстве. Все степени свободы равноправны.

Общее число степеней свободы

(2.8)

где - число степеней свободы поступательного движения;

- число степеней свободы вращательного движения;

- число степеней свободы колебательного движения;

i_кп - число степеней свободы колебаний точки при поступательном движении;

i_квр - число степеней свободы колебаний точки при вращательном движении.

Молекулы газа имеют число степеней свободы:

а) одноатомная - i = 3 (три степени свободы поступательного движения);

б) двухатомная при упругой связи между атомами - i = 6;

в) двухатомная при жёсткой связи между атомами - i = 5;

г) трёхатомная молекула при жёсткой связи между атомами - i = 6.

Теорема о равномерном распределении энергии по степеням свободы: на любую степень свободы приходится в среднем одинаковая энергия, равная , а молекула, обладающаяi степенями свободы, обладает энергией

(2.9)

где i = i_п + i_вр + i_к.

Внутренняя энергия произвольной массы газа m складывается из энергии отдельных молекул:

, (2.10)

где  - молярная масса газа.

Теплоемкость - физическая величина, численно равная количеству теплоты, которое необходимо сообщить веществу для нагревания его на один градус.

Удельная теплоёмкость "c" - физическая величина, численно равная количеству теплоты, которое необходимо сообщить единице массы вещества для нагревания её на один градус.

Молярная теплоёмкость "C" - физическая величина, численно равная количеству теплоты, которое необходимо сообщить одному молю вещества, чтобы увеличить его температуру на один градус:

. (2.11)

Удельная теплоёмкость при постоянном объеме"c_v" - физическая величина, численно равная количеству теплоты, которое необходимо сообщить единице массы вещества для нагревания её на один градус в условиях постоянного объема:

(2.12)

Удельная теплоёмкость при постоянном давлении "c_p" - физическая величина, численно равная количеству теплоты, которое необходимо сообщить единице массы вещества для нагревания её на один градус в условиях постоянного давления:

. (2.13)

Молярная теплоёмкость при постоянном объеме "C_v" - физическая величина, численно равная количеству теплоты, которое необходимо сообщить одному молю вещества, чтобы увеличить его температуру на один градус в условиях постоянного объема:

. . (2.14)

Молярная теплоёмкость при постоянном давлении "C_p" - физическая величина, численно равная количеству теплоты, которое необходимо сообщить одному молю вещества, чтобы увеличить его температуру на один градус в условиях постоянного давления:

, . (2.15)

Отношение молярных и удельных теплоемкостей :

(2.16)

Средняя квадратичная скорость молекул (для газа массой "m", находящегося в состоянии равновесия, при T = const) остаётся постоянной:

или , (2.17)

где N_i - число молекул, обладающих скоростью v_i;

N - число всех молекул.

Наиболее вероятная скорость - скорость движения молекул, которая характеризует положение максимума функции распределения Максвелла:

(2.18)

Средняя арифметическая скорость

(2.19)

Относительная скорость применяется для расчета числа молекул, движущихся со скоростями в интервале от v до v + dv:

u = v/v_в. (2.20)

Закон распределения молекул идеального газа по скоростям в стационарном состоянии (распределение Максвелла):

(2.21)

где dn_v - среднее число молекул в единице объема со скоростями в интервале от v до v + dv;

n - число молекул в единице объема.

Функция распределения (доля молекул от их общего числа отнесена к некоторому интервалу скоростей):

или , (2.22)

где dn_v/ndv - функция распределения.

Свободные пробеги молекул - прямолинейные участки траектории, проходимые молекулой между двумя последовательными соударениями.

Средняя длина свободного пробега молекулы – среднее расстояние, проходимое молекулой между двумя соударениями:

(2.23)

где Z - число соударений;

v - средняя скорость молекулы;

k - постоянная Больцмана;

d - диаметр молекулы;

p - давление;

T - абсолютная температура.

Среднее число соударений - число соударений молекул <Z>, численно равное отношению средней скорости движения молекул <v> к средней длине свободного пробега:

, (2.24)

Эффективный диаметр молекулы d - минимальное расстояние, на которое сближаются при столкновении центры 2-х молекул.

Эффективное сечение - величина равная

 = d². (2.25)

Барометрическая формула показывает, что давление убывает с высотой тем быстрее, чем тяжелее газ и чем ниже его температура:

(2.26)

Закон распределения молекул газа по высоте в поле сил тяготения (распределение Больцмана):

, , (2.27)

где n_o - число молекул в единице объема в том месте, где потенциальная энергия молекул равна нулю;

n - число молекул в единице объема в тех точках пространства, где потенциальная энергия молекул равна W_p.

Распределение Максвелла-Больцмана - благодаря этому распределению можно определить долю молекул идеального газа, имеющих скорости в интервале от v до v + dv и обладающих потенциалом  = gh во внешнем силовом поле:

, (2.28)

где v_в - наиболее вероятная скорость, значению которой соответствует максимум кривой Максвелла.

Зависимость плотности газа от высоты:

; , (2.29)

где m_o - масса одной молекулы.

2.3. Основные положения и законы термодинамики

Первое начало термодинамики - закон сохранения и превращения энергии, которым сопровождаются термодинамические процессы – количество тепла, подводимого к системе, идет на изменение ее внутренней энергии и работу, производимую системой против внешних сил:

, (2.30)

где dU - изменение внутренней энергии системы;

Q - элементарное количество тепла, подводимого к системе;

A - элементарная работа, совершаемая системой.

Изотермический процесс - процесс, протекающий при постоянной температуре (T = const). При изотермическом процессе все подводимое к системе тепло идет на совершение этой системой работы , при этом dU = C_vdT = 0,

а U = = const.

Работа, совершаемая произвольной массой m идеального газа при изотермическом процессе:

. (2.31)

Изобарический процесс – процесс, протекающий при постоянном давлении (p = const ). При этом подводимое к системе тепло идет как на изменение ее внутренней энергии, так и на совершение этой системой работы:

. (2.32)

Работа, совершаемая произвольной массой m идеального газа при изобарическом процессе:

. (2.33)

Изменение внутренней энергии произвольной массы m идеального газа при изобарическом процессе:

. (2.34)

Изохорический процесс – процесс, протекающий при постоянном объеме (V = const). При этом все подводимое к системе тепло идет на изменение ее внутренней энергии:

, (2.35)

Адиабатический процесс - процесс, протекающий без теплообмена или почти без теплообмена с окружающей средой. При этом работа может совершаться системой только за счет убыли ее внутренней энергии:

, . (2.36)

Уравнения адиабатического процесса (уравнения Пуассона):

; . (2.37)

Работа, совершаемая произвольной массой m идеального газа при адиабатическом расширении:

. (2.38)

Политропический процесс - такой процесс, при котором p и V связаны соотношением:

, (2.39)

где n - показатель политропы, принимающий любые значения от -  до + . В частности для изобарического процесса n = 0, изотермического - n = 1, адиабатического - n = , изохорического - n = .

Работа, совершаемая произвольной массой m идеального газа при политропическом процессе:

(2.40)

Работа, совершаемая идеальным газом при круговом процессе, равна разности работ при расширении А₁ и при сжатии А₂ газа и эквивалентна разности количеств тепла, подводимого к системе при расширении Q₁ и отводимого от нее при сжатии Q₂:

. (2.41)

Коэффициент полезного действия кругового процесса (цикла) - физическая величина, равная отношению работы цикла к работе, которую можно было бы совершить при превращении в нее всего количества тепла, подведенного к системе:

(2.42)

Цикл Карно - цикл, состоящий из двух изотермических и двух адиабатических процессов.

Работа, совершаемая произвольной массой m идеального газа в цикле Карно, - разность между работой, совершенной системой при расширении, и работой, совершенной над системой при ее сжатии:

. (2.43)

Коэффициент полезного действия цикла Карно  не зависит от природы вещества, а зависит лишь от температур, при которых теплота сообщается системе и отбирается от нее:

. (2.44)

Коэффициент полезного действия холодильной машины (холодильника):

(2.45)

Цикл Отто состоит из двух адиабат и двух изохор.

Цикл Дизеля состоит из двух адиабат, изохоры и изобары.

Энтропия - физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно полученному или отданному количеству теплоты, деленному на температуру, при которой произошел этот процесс:

. (2.46)

Связь энтропии системы с термодинамической вероятностью (соотношение Больцмана):

S = kln w, (2.47)

где k - постоянная Больцмана.

Изменение энтропии системы при переходе из одного состояния в другое

. (2.48)

Изменение энтропии системы при переходе из одного состояния в другое:

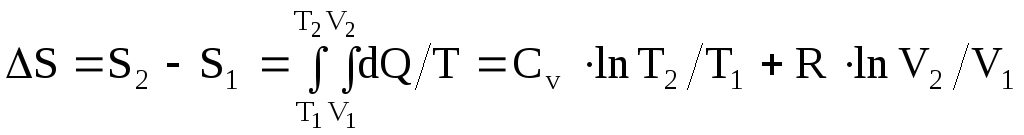. (2.49)

Изменение энтропии системы при изотермическом процессе:

. (2.50)

Изменение энтропии системы при изобарическом процессе:

. (2.51)

Изменение энтропии системы при изохорическом процессе:

. (2.52)

Изменение энтропии системы при адиабатическом процессе:

S = 0, . (2.53)

Изменение энтропии системы, совершающей цикл Карно:

, (2.54)

где S_р - изменение энтропии рабочего тела;

S_н, S_х - изменение энтропии нагревателя и холодильника;

S_пр - изменение энтропии "потребителя работы".

В случае совершения системой обратимого цикла Карно энтропия замкнутой системы не изменяется:

S_обр = 0 или S_обр=const. (2.55)

В случае совершения системой необратимого цикла Карно энтропия замкнутой системы возрастает:

S  0; ; . (2.56)

Для произвольных процессов, происходящих в замкнутой системе, энтропия системы для любых происходящих в ней процессов не может убывать:

S  0 или , (2.57)

где знак равенства справедлив для обратимых процессов, а знак неравенства - для необратимых.

Второе начало термодинамики: в изолированной системе возможны только такие процессы, при которых энтропия системы возрастает или невозможен процесс, единственным результатом которого является превращение в работу теплоты, полученной от нагревателя:

. (2.58)

Термодинамические потенциалы - определенные функции объема V, давления p, температуры T, энтропии S, числа частиц системы N и других макроскопических параметров x, характеризующих состояние термодинамической системы:

а) внутренняя энергия - энергия системы, зависящая от ее внутреннего состояния. Она является однозначной функцией независимых переменных, определяющих это состояние, например температуры T и объема V (или давления p):

U = U(S,V,N,x). (2.59)

Изменение внутренней энергии системы U определяется лишь ее значениями в начальном и конечном состояниях:

. (2.60)

б) энтальпия (теплосодержание) характеризует состояние макроскопической системы в термодинамическом равновесии при выборе в качестве основных независимых переменных энтропии S и давления p:

H = H(S,p,N,x). (2.61)

Энтальпия системы равна сумме энтальпий составляющих ее частей.

Связь энтальпии с внутренней энергией U системы:

, (2.62)

где V - объем системы.

Полный дифференциал энтальпии (при неизменных N и x) имеет вид

. (2.63)

Связь энтальпии с температурой, объемом и теплоемкостью (при постоянном давлении) системы:

; ; C_p=(dH/dt). (2.64)

Изменение энтальпии (H) равно количеству теплоты, которое сообщают системе или отводят от нее при постоянном давлении, поэтому значения H характеризуют тепловые эффекты фазовых переходов (плавления, кипения и т. д.), химических реакций и других процессов, протекающих при постоянном давлении.

в) свободная энергия - одно из названий изохорно-изотермического термодинамического потенциала или Гельмгольца энергии. Представляет собой ту часть внутренней энергии системы, которая превращается во внешнюю работу при обратимых изотермических процессах F = F(V,T,N,x):

, (2.65)

где TS - связанная энергия.

Связанная энергия представляет собой ту часть внутренней энергии, которая не может быть передана в виде работы при изотермическом процессе:

TS = U - F. (2.66)

Изменение (уменьшение) свободной энергии при необратимых изотермических процессах определяет наибольшую величину работы, которую может совершить система:

; . (2.67)

г) энергия Гиббса - изобарно-изотермический потенциал, свободная энтальпия, характеристическая функция термодинамической системы при независимых параметрах p, T и N - G. В изотермически равновесном процессе, при постоянном давлении, убыль энергии Гиббса системы равна полной работе системы за вычетом работы против внешнего давления (т.е. равна максимальному значению "полезной" работы):

G = G(p,T,N,x); . (2.68)

Связь энергии Гиббса со свободной энергией:

. (2.69)

д) химический потенциал - физическая величина, равная энергии Гиббса отдельно взятой частицы.

Третье начало термодинамики (теорема Нернста): изменение энтропии системы (S) при любых обратимых изотермических процессах, совершаемых между двумя равновесными состояниями при температурах, приближающихся к абсолютному нулю, стремится к нулю. При помощи последовательности термодинамических процессов нельзя достичь температуры, равной абсолютному нулю:

. (2.70)

Термодинамика неравновесных процессов - общая теория макроскопического описания неравновесных процессов. Основная задача термодинамики неравновесных процессов - количественное изучение этих процессов для состояний, не сильно отличающихся от равновесного состояния.

Закон сохранения массы:

, (2.71)

где  - плотность многокомпонентной системы;

v - гидродинамическая скорость среды (средняя скорость переноса массы), зависящая от координат и времени;

∙v - поток массы.

Закон сохранения массы для концентрации какого-либо компонента :

, (2.72)

где c_k - концентрация компонента;

_k - плотность компонента;

 - плотность среды;

J_k = _k(v_k - v) - диффузионный поток;

v_k - гидродинамическая скорость (средняя скорость переноса массы) компонента.

Закон сохранения импульса: изменение импульса элементарного объема может происходить за счет сил, вызванных градиентом внутренних напряжений в среде P_,, и внешних сил F_k.

Закон сохранения энергии представляет собой первое начало термодинамики в термодинамике неравновесных процессов.

Уравнение баланса энтропии: в термодинамике неравновесных процессов принимается, что энтропия элементарного объема является такой же функцией от внутренней энергии, удельного объема и концентрации, как и в состоянии полного равновесия:

, (2.73)

где  - скорость возрастания энтропии;

 - плотность вещества;

s – энтропия элементарного объема (локальная энтропия);

J_s – плотность потока энтропии.

2.4. Реальные газы. Фазовые равновесия и превращения

Реальный газ – газ, свойства которого зависят от взаимодействия частиц и их собственного объема, что особенно проявляется при высоких давлениях и низких температурах.

Уравнение состояния реальных газов (уравнение Ван дер Ваальса) для произвольной массы газа:

, (2.74)

где "а" - поправка Ван дер Ваальса на влияние сил межмолекулярного взаимодействия (на внутреннее давление);

"в" - поправка Ван дер Ваальса на собственный объем молекул;

μ - молекулярная масса газа;

m - масса газа.

Внутренняя энергия реального газа состоит из кинетической энергии поступательного и вращательного движения молекул Е_k и потенциальной энергии их взаимодействия Е_p.

Потенциальная энергия взаимодействия одного моля молекул реального газа имеет отрицательный знак, т.к. молекулярные силы, создающие внутреннее давление p^', являются силами притяжения:

. (2.75)

Изменение потенциальной энергии реального газа (для моля) равно работе, которую совершает внутреннее давление p при расширении газа от объёма V₁ до V₂:

. (2.76)

Кинетическая энергия молекул реального газа (для моля) согласно теореме о равном распределении энергии по степеням свободы (в некотором приближении):

. (2.77)

Внутренняя энергия одного моля реального газа:

. (2.78)

Изменение температуры реального газа при адиабатическом расширении (при этом газ охлаждается) или сжатии (при этом газ нагревается):

. (2.79)

Эффект Джоуля - Томсона - изменение температуры реального газа при расширении через пористую перегородку. Если газ при расширении охлаждается, то эффект Джоуля-Томсона называется положительным, если нагревается - отрицательным.

Фаза - равновесное (в термодинамике) состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества.

Фазовые превращения - переход вещества из одной фазы в другую, связанный с качественными изменениями свойств вещества при изменении внешних условий.

Фазовое равновесие - одновременное существование термодинамически равновесных фаз в многофазной системе.

Правило фаз Гиббса: в веществе, состоящем из n компонентов, одновременно может существовать не более чем (n + 2) равновесных фаз.

Число физических параметров системы, которые можно изменять, не нарушая фазовое равновесие:

L = n + 2 - , (2.80)

где  - число фаз, находящихся в равновесии.

Уравнение Клапейрона-Клаузиуса определяет изменение температуры фазового перехода при бесконечно малом изменении давления:

; ;, (2.81)

где Q - теплота фазового перехода;

T - температура перехода;

dp/dT - производная от давления по температуре;

dT/dp - производная от температуре по давлению;

(V₂ - V₁) - изменение объема вещества при переходе его из первой фазы во вторую.

Метастабильное состояние - состояние неустойчивого равновесия физической макроскопической системы (фазы). В таком состоянии система может находиться длительное время, не переходя в более устойчивое (при данных условиях) состояние (фазу).

Линии (поверхности) равновесия фаз - графики, изображающие зависимость одних термодинамических переменных от других в условиях фазового равновесия.

Диаграммы состояния - совокупность линий (поверхностей) равновесия фаз.

Тройная точка - точка пересечения одной линии (поверхности) равновесия фаз с другой.

Критическая точка - точка на диаграмме состояния, соответствующая критическому состоянию вещества. Состояние вещества в критической точке характеризуется критическими значениями температуры T_k, давления p_k и объема V_k.

Критическая точка в случае двухфазного равновесия - точка окончания линии (поверхности) равновесия фаз.

Точка перехода - значение температуры, давления или какой-либо другой величины, при которой происходит фазовый переход.

Фазовый переход первого рода характеризуется тем, что при его осуществлении поглощается или выделяется определенное количество теплоты, которое называют теплотой фазового перехода. Значение таких термодинамических величин вещества, как плотность, концентрация компонентов, изменяется скачком.

Фазовый переход второго рода - такой переход, при котором некоторая физическая величина, равная нулю с одной стороны от точки перехода, постепенно растет при удалении от точки перехода в другую сторону, при этом плотность вещества изменяется непрерывно и не происходит поглощения или выделения тепла.

2.5. Кинетические явления (явления переноса)

Кинетические явления (явления переноса) - необратимые процессы, сопровождающиеся переносом какой-либо физической величины, в результате перехода любой системы из неравновесного состояния в равновесное состояние.

Кинетические явления в молекулярной физике - вязкость, теплопроводность, диффузия.

Вязкость (внутреннее трение) - явление переноса, в результате которого происходит перенос количества движения (импульса) молекул из одного слоя газа или жидкости в другой.

Сила внутреннего трения в жидкости или газе определяется по формуле Ньютона:

, (2.82)

где  - коэффициент вязкости;

S - площадь соприкасающихся слоев жидкости или газа;

dv/dz - градиент скорости течения жидкости или газа в направлении, перпендикулярном направлению течения;

Коэффициент динамической вязкости - физическая величина, численно равная силе внутреннего трения между двумя слоями жидкости или газа единичной площади при градиенте скорости, равном единице:

или , (2.83)

где n₀ - число молекул в единице объема;

u - средняя скорость теплового движения молекул;

m - масса молекулы;

 - средняя длина свободного пробега молекул;

 = n₀∙m - плотность жидкости или газа.

Коэффициент кинематической вязкости - отношение динамической вязкости к плотности вещества:

ν = η/ρ. (2.84)

Диффузия - процесс взаимного проникновения молекул (атомов) постороннего вещества, обусловленный их тепловым движением. Диффузия всегда сопровождается переносом массы вещества. Она характерна для газов, жидкостей и твердых тел.

Самодиффузия - процесс взаимного проникновения собственных молекул (атомов), обусловленный их тепловым движением.

Закон диффузии (первый закон Фика):

, (2.85)

где D - коэффициент диффузии;

dс/dz - скорость изменения (градиент) концентрации в направлении z;

"минус" - показывает, что масса переносится в направлении убывания концентрации данной компоненты.

Коэффициент диффузии - физическая величина, числено равная массе переносимого вещества через единичную площадку в единицу времени при градиенте концентрации, равном единице:

, (2.86)

где <v> - средняя арифметическая скорость молекул;

<> - средняя длина свободного пробега молекул.

Теплопроводность - процесс переноса энергии между контактирующими телами или двумя поверхностями одного и того же тела, возникающий из-за разности температур.

Закон теплопроводности (закон Фурье) - количество тепла dQ, перенесенное через площадку dS за время dt:

, (2.87)

где æ - коэффициент теплопроводности;

dT/dz - скорость изменения (градиент) температуры в направлении z.

Коэффициент теплопроводности - физическая величина, которая показывает, какое количество тепла переносится через единичную площадку в единицу времени при градиенте температур, равном единице:

, (2.88)

где c_v – удельная теплоемкость при постоянном объеме.

Тепловой поток - физическая величина, которая показывает, какое количество тепла, переносится в единицу времени через площадь dS при градиенте температуры dT/dz:

. (2.89)

Связь между коэффициентами теплопроводности, диффузии и вязкости:

;  = D; . (2.90)