5. Электромагнитные явления

5.1. Магнитное поле и его характеристики. Основные понятия, определения и законы

Магнитостатика - раздел теории электромагнитного поля, в котором изучаются свойства стационарного магнитного поля (полей постоянных электрических токов или поля постоянных магнитов) а также движение заряженных частиц в стационарном магнитном поле.

Теорема эквивалентности поля магнитных зарядов и поля постоянных электрических токов (теорема Ампера)- магнитное поле предельно тонкого плоского магнита ("магнитного листка"), образованного из одинаково ориентированных элементарных магнитиков, тождественно полю замкнутого (кругового) линейного тока, текущего по контуру этого магнита.

Макротоки - упорядоченное движение электрических зарядов в объеме проводника.

Микротоки обусловлены наличием в атомах вещества электронов, вращающихся вокруг ядер с большой скоростью (10¹⁵ с^-1). Движение каждого электрона эквивалентно замкнутому контуру с током.

Орбитальный магнитный момент микротока вещества

p_m = IS, (5.1)

где I - величина эквивалентного тока (микротока);

S - площадь орбиты электрона.

Пробный ток (пробный контур) – ток, существующий в плоском замкнутом контуре малых размеров (круговой ток). Положение этого контура в пространстве определяется с помощью положительной нормали, связанной с током в контуре правилом правого винта.

Магнитный момент пробного тока (пробного контура) p_m – векторная физическая величина, характеризующая свойства пробного контура, численно равная произведению величины тока в контуре на площадь, охватываемую контуром:

p_m = IS, (5.2)

где I - величина тока в контуре;

S – площадь, охватываемая контуром.

Вращающий момент, действующий на пробный контур, пропорционален его магнитному моменту, синусу угла  между направлением положительной нормали и направлением магнитного поля в данном месте пространства:

M_вр~p_m∙sin = I∙S∙sin. (5.3)

Связь вращающего момента, действующего на пробный контур в магнитном поле с индукцией магнитного поля:

а) в скалярной форме

M_вр = p_mBsin, (5.4)

б) в векторной форме

, (5.5)

где p_m – магнитный момент пробного контура;

B – вектор индукции магнитного поля;

 - угол между векторами p_mи B.

Индукция магнитного поля B - векторная физическая величина, численно равная вращающему моменту, действующему на пробный контур, помещенный перпендикулярно к направлению магнитного поля в данную точку, магнитный момент которого равен единице. Характеризует силовое воздействие магнитного поля макро - и микротоков на движущиеся электрические заряды. При прочих равных условиях и одном и том же токе в проводнике величина B в различных средах различна:

. (5.6)

Напряженность магнитного поля H - характеристика магнитных полей, порождаемых только макротоками. Напряженность магнитного поля не зависит от свойств среды.

Связь напряженности магнитного поля H с магнитной индукцией B:

B = ₀H, (5.7)

где ₀- магнитная постоянная;

 - относительная магнитная проницаемость среды, которая показывает, во сколько раз магнитное поле макротоков усиливается за счет магнитных полей микротоков.

Вектор намагниченности J - характеристика магнитных полей микротоков вещества. Характеризует магнитное состояние макроскопического тела. Определяется как магнитный момент единицы объема тела:

а) в случае однородно намагниченного тела

; (5.8)

б) в случае неоднородно намагниченного тела

, (5.9)

где dV – физически бесконечно малый объём, взятый в окрестности рассматриваемой точки;

p_m – магнитный момент отдельной молекулы Суммирование производится по всем молекулам, заключённым в объёме dV

В вакууме микротоки (молекулярные токи) отсутствуют и вектор намагниченности J равен нулю:

J_вак = 0. (5.10)

В отсутствие внешнего магнитного поля магнетик (при H = 0) вектор намагниченности

J = 0. (5.11)

В веществах во внешнем магнитном поле (кроме так называемых ферромагнетиков и не слишком сильных полях) зависимость J от H является практически линейной:

J = _mH, (5.12)

где _m - магнитная восприимчивость вещества (характеризует его магнитные свойства).

Связь между векторами B, H и J:

B/₀ = H +J; B= ₀ (1 + _m)H = ₀H, (5.13)

где  = (1 + _m) - относительная магнитная проницаемость среды.

Принцип суперпозиции магнитных полей: магнитное поле нескольких токов характеризуется результирующими векторами B или H, которые определяются соотношениями

B = B₁ + B₂ + ....+ B_n = ; H = H₁ + H₂ +....+ H_n = (5.14)

Индукция магнитного поля созданного (закон Био-Савара-Лапласа):

а) объёмным элементом тока

; (5.15)

б) линейным элементом тока

. (5.16)

Результирующая индукция магнитного поля для замкнутых постоянных токов

 (5.17)

Индукция и напряженность магнитного поля:

а) прямолинейного бесконечно длинного проводника с током

; ; (5.18)

б) при симметричном расположении точки М относительно концов проводника (cos₁ = - cos₂)

; ; (5.19)

в) бесконечно длинного проводника с током (0, )

; , (5.20)

где I - сила тока в проводнике;

r - расстояние от элемента проводника dl до рассматриваемой точки поля;

₁, ₂ - углы между направлением тока в проводнике и направлением на рассматриваемую точку поля;

- численное значение вектора, равного элементу проводника, направление которого совпадает с направлением тока;

г) на оси кругового проводника радиусом R, в котором существует ток I:

;  (5.21)

где R - радиус кругового проводника;

r₀ - расстояние от центра до рассматриваемой точки поля на оси кругового проводника;

д) в центре кругового проводника

B = ₀I/2R; H = I/2R; (5.22)

е) внутри соленоида в произвольной точке А (соленоид - катушка цилиндрической формы из проволоки, витки которой намотаны в одном направлении и прилегают плотно друг к другу)

, (5.23)

где  - длина соленоида;

N – число витков;

R – радиус соленоида;

₁, ₂ – углы, под которыми видны концы соленоида из рассматриваемой точки А внутри его;

ж) внутри бесконечно длинного соленоида (₂0 и ₁180⁰)

B = ₀IN/; H = IN/ =In, (5.24)

где n = N/ - число витков на единице длины соленоида;

I - величина тока в соленоиде;

з) внутри соленоида конечной длины

B = ₀nI/2; H = nI/2; (5.25)

и) внутри тороида на его оси (тороид - соленоид, свитый в кольцо)

B = ₀IN/l = ₀In = ₀IN/2r; H = IN/l = In = IN/2r; (5.26)

к) внутри тороида на произвольном расстоянии r от его центра

B = ₀nIR/r; H = nIR/r, (5.27)

где l = 2r - длина оси тороида;

R – радиус тороида по средней линии;

r - радиус тороидального кольца;

I - сила тока;

N - число витков тороида;

n - число витков на единицу длины тороида.

Циркуляция вектора индукции магнитного поля по замкнутому контуру L (или просто циркуляцией вектора индукции магнитного поля) – физическая величина, определяемая линейным интегралом:

, (5.28)

где dl – вектор элементарной длины замкнутого контура, направленной вдоль обхода контура;

B_l = Bcos - составляющая вектора B в направлении касательной к контуру (с учетом выбранного направления обхода);

 - угол между векторами B и dl.

Циркуляция вектора напряженности магнитного поля по замкнутому контуру L (или просто циркуляция вектора напряженности магнитного поля) - физическая величина, определяемая линейным интегралом:

, (5.29)

где dl – вектор элементарной длины замкнутого контура, направленной вдоль обхода контура;

H_l = Hcos - составляющая вектора H в направлении касательной к контуру (с учетом выбранного направления обхода);

 - угол между векторами H и dl.

Закон полного тока (теорема о циркуляции индукции магнитного поля) в интегральной форме: циркуляция вектора индукции магнитного поля по замкнутому контуру L равна произведению ₀ на алгебраическую сумму токов, охватываемых контуром (направление обхода контура и направление тока должны быть связаны между собой правилом правого винта):

, (5.30)

где n – число проводников с токами, охватываемых контуром L произвольной формы.

Следствия из закона полного тока:

1) если направление обхода контура и направление тока в проводнике не связаны между собой правилом правого винта, то значение циркуляции вектора магнитной индукции, сохранив величину, изменит знак;

2) если контур, расположенный в магнитном поле, не охватывает ток или алгебраическая сумма токов внутри замкнутого контура равна нулю:

. (5.31)

Закон полного тока (теорема о циркуляции индукции магнитного поля) в дифференциальной форме справедлив для произвольных токов и контуров:

rotB=₀j 5.32

Условие непотенциальности магнитного поля (вихревого характера магнитного поля):

. (5.33)

Поток магнитной индукции (магнитный поток) через площадку dS - физическая величина, численно равная произведению проекции B на направление положительной нормали n и величины этой площадки dS:

dФ_m=B_ndS=BdScos, (5.34)

где  - угол между векторами B и n;

B_n = Bcos - проекция вектора B на направление положительной нормали к площадке dS.

Полный поток магнитной индукции через некоторую поверхность S

 (5.35)

Для однородного магнитного поля и плоской площадки S

Ф_m = B_nS. (5.36)

Теорема Остроградского-Гаусса для магнитных полей:

 (5.37)

Индукция магнитного поля B в магнитной цепи, состоящей из стального сердечника с воздушным (вакуумным) зазором:

, (5.38)

где l_c l_В - соответственно длина стального и воздушного участков цепи;

_с, _В - их магнитные проницаемости;

I - ток в обмотке цепи;

N - число витков обмотки.

Закон Ома для магнитных цепей:

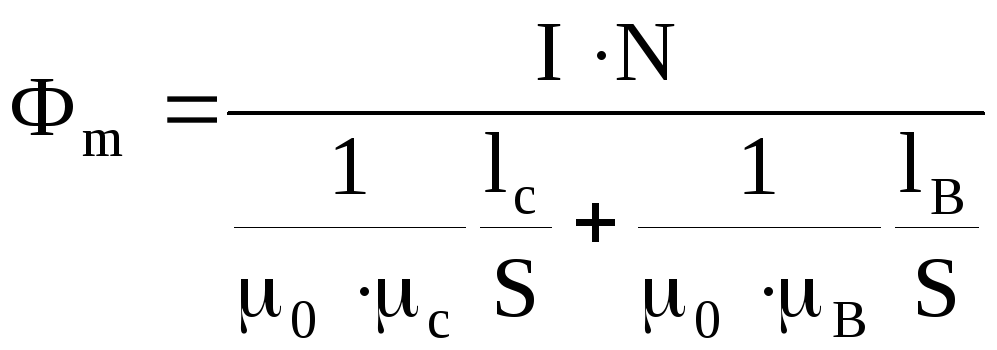
, (5.38)

где IN = E_м - магнитодвижущая сила;

R_мс = - магнитное сопротивление цепи сердечника;

R_мв = - магнитное сопротивление цепи воздушного зазора;

R_м = R_мс + R_мв - полное сопротивление магнитной цепи.

Законы (правила) Кирхгофа для магнитных цепей:

1. Первый: Алгебраическая сумма магнитных потоков в участках цепи, сходящихся в узле, равна нулю:

 (5.39)

Примечание: знак Ф_мi определяется направлением соответствующих линий B. Если линии вектора B сходятся в узле, Ф_мi - положителен, если они выходят из узла, Ф_мi - отрицателен.

2. Второй: В любом замкнутом магнитном контуре, произвольно выбранном в разветвленной магнитной цепи, алгебраическая сумма произведений магнитных потоков на магнитное сопротивление соответствующих участков цепи равна алгебраической сумме магнитодвижущих сил этого контура:

 (5.40)

При последовательном соединении магнитопроводов полное магнитное сопротивление равно сумме магнитных сопротивлений отдельных последовательно соединенных участков:

R_м = . (5.41)

При параллельном соединении величина, обратная сопротивлению разветвленной части магнитной цепи, равна сумме обратных величин магнитных сопротивлений отдельных ветвей:

 (5.42)

5.2. Силы, действующие на ток в электромагнитном поле

Сила, действующая в магнитном поле на элемент объема тела dV:

dF =e [vB]∙dN = n∙e∙[vB]dV = [jB]dV, (5.43)

где e- величина заряда электрона;

n - концентрация свободных электронов;

dN = n∙dV - число заряженных частиц в объеме dV;

j = nev - плотность тока;

v - скорость направленного движения свободных электронов;

B - индукция магнитного поля.

Сила (сила Ампера), действующая на проводник с током в магнитном поле (закон Ампера):

а) на каждый элемент проводника dl

dF = I[dlB]; (5.44)

б) на проводник конечной длины

, (5.45)

где l длина проводника.

Величина силы, действующей со стороны однородного магнитного поля на прямолинейный проводник с током:

F = I∙B∙l∙sin. (5.46)

Величина силы, действующей со стороны неоднородного поля и проводника произвольной формы:

dF = I∙B∙dl∙sin. (5.47)

5.3. Работа по перемещению проводника и контура с током в магнитном поле

Работа по перемещению проводника с током в магнитном поле (работа, совершаемая силами Ампера), ток в котором постоянен, равна произведению силы тока на величину магнитного потока через поверхность, которую описывает проводник при своем движении:

dA = IdФ_m. (5.48)

Работа по перемещению проводника с током в магнитном поле (работа, совершаемая силами Ампера), ток в котором постоянен и проводник прямолинейный:

A = IФ_m. (5.49)

Работа, совершаемая силами Ампера при перемещении в магнитном поле контура, ток в котором постоянен, равна произведению силы тока на изменение магнитного потока через поверхность, ограниченную контуром:

dA = IdФ_m, (5.50)

где I - величина тока в контуре;

dФ_m - изменение магнитного потока.

Работа, совершаемая силами Ампера при перемещении в магнитном поле контура, ток в котором постоянен, а перемещаемый контур состоит из N витков:

dA = , (5.51)

где  = - потокосцепление или полный магнитный поток, пронизывающий N витков контура.

5.4. Магнитные свойства вещества (среды)

Диамагнетики - вещества (среда), намагничивающиеся во внешнем магнитном поле напряженностью H в направлении, противоположном направлению вектора H (приобретающие суммарный магнитный момент, который направлен противоположно вектору H).

Диамагнетизм (диамагнитный эффект) – свойства вещества намагничиваться навстречу направлению действующего на него внешнего магнитного поля. При этом вектор намагничивания J пропорционален напряженности внешнего магнитного поля H:

J =æ= æ, (5.52)

где æ=- диамагнитная восприимчивость вещества.

Примечания:

1) диамагнетизм - свойство, присущее любым веществам, так как он обусловлен действием внешнего магнитного поля на электронные орбиты атомов и молекул;

2) движение электронов по орбитам сопровождается появлением магнитного поля, направленного против внешнего поля и ослабляющего его (закон Ленца);

3) диамагнитный эффект не связан с появлением упорядоченности в расположении электронных орбит, поэтому диамагнитная восприимчивость æ не зависит от температуры;

4) диамагнитный эффект является реакцией вещества на воздействие внешнего магнитного поля.

Магнитный момент электрона, представляющего собой некоторый эквивалентный круговой ток:

p_m = I∙S = e∙r² = ev_or/2, (5.53)

где e - заряд электрона;

v_o - его скорость;

r - радиус орбиты;

 – частота, с которой электрон движется по орбите.

Магнитный момент электронной орбиты

p_m = (e/2m)mv₀∙r = (e/2m)p, (5.54)

где p = m∙v₀∙r - момент количества движения электрона на орбите.

Изменение магнитного момента электронной орбиты происходит за счет изменения скорости электрона:

, (5.55)

где m - масса электрона;

B₀ - индукция внешнего магнитного поля.

Прецессия Лармора - синхронное вращательное движение совокупности электронов изолированного атома под действием внешнего магнитного поля относительно оси, проходящей через центр атома параллельно направлению H. Вклад каждого электрона в диамагнитную восприимчивость æ_Д изолированного атома вычисляется по формуле

æ_Д=, (5.56)

где e - заряд электрона;

m - его масса;

c - скорость света в вакууме;

<r²> - средний квадрат расстояния электрона от ядра атома.

Парамагнетизм - свойство веществ (парамагнетиков), помещенных во внешнее магнитное поле, намагничиваться (приобретать магнитный момент) в направлении, совпадающем с направлением этого поля. Вещества, обладающие таким свойством, называют парамагнетиками. При этом намагниченность увеличивается по закону

J = æ_mH, (5.57)

где æ_m - магнитная восприимчивость вещества;

H - напряженность внешнего магнитного поля.

Парамагнетики - вещества (среда), намагничивающиеся во внешнем магнитном поле напряженностью H в направлении, совпадающем с направлением вектора H (приобретающие суммарный магнитный момент, который совпадает по направлению с вектором H).

Закон Кюри: в слабых полях и при низких температурах удельная магнитная восприимчивость парамагнитных веществ обратно пропорциональна температуре:

æ = , (5.58)

где æ = æ_m/ - удельная (массовая) магнитная восприимчивость;

æ_m - магнитная восприимчивость единицы объема вещества;

 - плотность вещества;

С = np_m²/3k - постоянная Кюри;

n – число молекул в единице объема;

k - постоянная Больцмана;

T – абсолютная температура.

Закон Кюри-Вейса обобщает закон Кюри для веществ, в которых носители магнитных моментов взаимодействуют:

æ = C'/(T - ), (5.59)

где C' – постоянная, которая для свободных магнитных ионов данного вида вещества совпадает с постоянной Кюри;

 - константа вещества, характеризующая взаимодействие ионов между собой и с внутрикристаллическим полем.

Магнитный момент единицы массы вещества в слабых магнитных полях при температуре T:

J' = J/ = N∙²∙H/3k∙T, (5.60)

где N - число молекул.

В сильных магнитных полях и при низких температурах (когда H/T  и тепловое движение не нарушает ориентацию магнитных моментов) возможно насыщение (все атомные моменты ориентированы одинаково), и закон Кюри не выполняется. При этом

J'∙N. (5.61)

Закон Кюри для парамагнетизма ядер:

æ_моль =  (5.62)

где æ_моль - магнитная восприимчивость 1 моля вещества;

p_{m, эфф} - эффективный магнитный момент ядра;

C_я - ядерная постоянная Кюри;

N - число ядер на моль.

Магнитный момент частицы, обладающей зарядом ^"e^" и массой ^"m^" (магнетон Бора):

_Б = _o = , (5.63)

где _Б – магнетон Бора;

h - постоянная Планка;

c - скорость света в вакууме.

Ядерный магнетон

. (5.64)

Спиновый магнитный момент

_S = 2_Б . (5.65)

Парамагнитная восприимчивость диэлектриков согласно классической теории Ланжевена определяется формулой

æ_L = , (5.66)

где N - число парамагнитных атомов в 1 моле вещества;

_а - магнитный момент атома.

Магнитная восприимчивость диэлектриков с точки зрения квантовой теории парамагнетизма учитывает пространственное квантование момента _а и при _аH<<kT приводит к следующей формуле:

æ_L = , (5.67)

где j - квантовое число, определяющее полный момент импульса атома;

g_L - множитель Ланде.

Парамагнитная восприимчивость одного моля:

а) для полупроводников æ_п обусловлена электронами проводимости, в простейшем случае зависит от температуры T экспоненциально:

æ= AT^1/2exp(-E/kT), (5.68)

где A - константа вещества;

E - ширина запрещенной зоны полупроводника;

б) для металлов - без учета диамагнетизма Ландау и взаимодействия электронов

æ, (5.69)

где E_o - энергия Ферми;

_э - магнитный момент электрона.

Ядерный парамагнетизм при отсутствии сильного взаимодействия между спинами ядер и электронными оболочками атомов возникает, в основном, за счет двух факторов:

1) орбитального движения электронов (полный орбитальный магнитный момент атома является суммой орбитальных магнитных моментов отдельных электронов);

2) наличия у каждого электрона собственного магнитного момента, связанного со спином электрона, т.е. собственного механического момента электрона; характеризуется величиной

æ_я = . (5.70)

Ферромагнетик – вещество (среда), в котором ниже определенной температуры (точки Кюри) устанавливается ферромагнитный порядок магнитных моментов атомов или ионов (в неметаллических кристаллах) или магнитных моментов коллективизированных электронов (в металлических кристаллах).

Ферромагнетизм - магнитоупорядоченное состояние вещества, при котором все магнитные моменты атомов в веществе параллельны.

Магнитная восприимчивость æ_k ферромагнетиков положительна и æ_k>>0.

Точка Кюри – температура, при которой намагниченность насыщения J_s равна нулю.

Обменное взаимодействие – взаимодействие, приводящее к ферромагнетизму, которое характеризуется напряженностью эффективного молекулярного поля:

H_эфф = A∙J_s. (5.71)

Энергия обменного взаимодействия U квадратично зависит от J_s:

U = -H_эффJ_s = , (5.72)

где A - постоянная молекулярного поля (A>0);

J_s - намагниченность насыщения.

Закон Блоха: с точки зрения теории спиновых волн, при низких температурах самопроизвольная намагниченность убывает с ростом температуры

J_s = J_so(1 - T^3/2), (5.73)

где J_so - намагниченность насыщения при T = 0.

Домены – области однородной намагниченности в ферромагнетике в отсутствие внешнего магнитного поля.

Коэрцитивная сила H_c – величина напряженности магнитного поля, в котором ферромагнетик, первоначально намагниченный до насыщения, размагничивается.

Остаточная индукция B_s – величина, характеризующая магнитное поле в ферромагнетике даже в отсутствие внешнего магнитного поля.

Остаточная намагниченность J_r – намагниченность J_r, которую имеет ферромагнетик при напряженности внешнего магнитного поля H = 0.

Намагничивание – процессы установления намагниченности, протекающие в веществе при действии на него внешнего магнитного поля:

а) в диамагнетиках намагничивание состоит в возникновении микроскопических индукционных токов, создающих намагниченность, направленную против внешнего магнитного поля;

б) в парамагнетиках намагничивание состоит из ориентации хаотически колеблющихся магнитных моментов атомов или ионов в направлении внешнего магнитного поля;

в) в ферромагнетиках намагничивание состоит в переориентации векторов намагниченности доменов в направлении внешнего магнитного поля. Включает процессы смещения, вращения и парапроцесс.

Процесс смещения в многодоменном ферромагнетике заключается в перемещении границ между доменами.

Процесс вращения состоит в повороте векторов J_s в направлении вектора H внешнего магнитного поля.

Парапроцесс (истинное намагничивание) – возрастание абсолютной величины самопроизвольной намагниченности J_s ферро - и ферримагнетиков под действием внешнего магнитного поля H. Обусловлен ориентацией в поле H элементарных носителей магнетизма (спиновых и орбитальных магнитных моментов атомов или ионов), оставшихся не повернутыми в направлении результирующей намагниченности вследствие «дезорганизующего» действия теплового движения.

Кривые намагничивания – графики, таблицы и формулы, показывающие зависимость намагниченности J или магнитной индукции B от напряженности внешнего магнитного поля H.

Ферримагнетик - вещества, в которых при температурах ниже точки Кюри T_c существует ферримагнитное упорядочение магнитных ионов.

Ферримагнетизм - магнитоупорядоченное состояние вещества, в котором магнитные моменты атомных носителей магнетизма образуют несколько магнитных подрешеток с магнитными моментами, направленными навстречу друг к другу или имеющими более сложную пространственную ориентацию; отличная от нуля векторная сумма намагниченностей подрешеток определяет самопроизвольную намагниченность вещества J_s.

Антиферромагнетизм - магнитоупорядоченное состояние вещества, характеризующееся тем, что магнитные моменты соседних частиц вещества - атомных носителей магнетизма - ориентированы навстречу друг другу (антипараллельно), и поэтому намагниченность тела в целом в отсутствие магнитного поля равна нулю.

Магнитострикция - изменение формы и размеров ферромагнетиков и ферримагнетиков при их намагничивании.

Магнитоупругий эффект (эффект Виллари) - обратное по отношению к магнитострикции явление - изменение намагниченности ферромагнитного образца при деформации.

Магнитное охлаждение - метод получения температур ниже 1К путем адиабатического размагничивания парамагнитных веществ.

Магнетокалорический эффект - изменение температуры магнетика при адиабатическом изменении напряженности магнитного поля H, в котором он находится.

На границе раздела двух магнетиков (сред):

а) нормальные составляющие вектора B и тангенциальные составляющие вектора H непрерывны:

B_1n = B_2n, H_2t = H_1t; (5.74)

б) закон преломления силовых линий векторов B и H при переходе через границу раздела двух магнетиков имеет вид

 (5.75)

5.5. Основные уравнения термодинамики магнетиков

Первое начало термодинамики для магнетика:

Q = dU + A, (5.76)

где Q - количество сообщенного тепла;

dU - изменение внутренней энергии;

A - работа магнетика, которая складывается из работы A' = pdV против внешнего давления и работы магнитного поля 

Основные уравнения термодинамики магнетиков для:

а) свободной энергии

F = U - TS, dF = -SdT + (H dB)/4; (5.77)

б) термодинамического потенциала

Ф = F - HB/4; dФ = -SdT - (B dH)/4; (5.78)

в) энтальпии

I = U - HB/4, dI = TdS - (B dH)/4; (5.79)

г) изменения внутренней энергии

dU = TdS + (H dB)/4; (5.80)

д) внутренней энергии магнетика U

. (5.81)

Изменение температуры магнетика в зависимости от изменения напряженности магнитного поля

, (5.82)

где C_H = ip/(2T) - теплоемкость единицы объема магнетика при постоянной напряженности магнитного поля (молярная теплоемкость ферромагнетика при постоянном магнитном поле).

Изменение температуры парамагнетика

; . (5.83)

5.6. Явление электромагнитной индукции. Самоиндукция

Электромагнитная индукция - возникновение электродвижущей силы E_i (ЭДС электромагнитной индукции - распределенной) в проводящем контуре, находящемся в переменном магнитном поле или движущимся в постоянном магнитном поле.

Основной закон электромагнитной индукции (закон Фарадея): при пересечении потока магнитной индукции отрезком проводника в нем возникает ЭДС электромагнитной индукции, которая прямо пропорциональна скорости изменения величины магнитного потока. В замкнутом проводнике возникает индукционный ток. При этом

E_i, (5.84)

где dФ/dt - скорость изменения магнитного потока.