
- •Оглавление
- •Структурные схемы планетарных зубчатых передач
- •А) редуктор Джемса;
- •2. Аналитическое определение передаточного отношения планетарного механизма
- •Методика выбора чисел зубьев колес
- •3.1. Редуктор Джемса (рис. 2,а)
- •1.Уравнение передаточного отношения
- •4. Условие соседства сателлитов.
- •3.2 Редуктор со сдвоенными сателлитами (рис.2,б)
- •3.3. Редуктор с двумя внешними зацеплениями (редуктор Давида)
- •3.4. Редуктор с двумя внутренними зацеплениями (рис. 3.Б)
- •Подставив сюда z3 из (3.25) и z4 из (3.26) и несколько преобразуя, получим:
- •3.5. Основные выводы и рекомендации.
- •4. Графический метод определения передаточного отношения планетарной передачи
- •5. Методика выполнения курсового проекта
- •Министерство образования российской федерации
Составитель
Б.В.Лушников
УДК 629.11.012.8
Проектирование
планетарных зубчатых механизмов:
Методические рекомендации к курсовому
проектированию по теории механизмов
и машин/ Курск. гос. техн. ун.-т; Сост.
Б.В.Лушников. Курск, 2001. 22 с.
Изложены
теоретические основы проектирования
планетарных зубчатых механизмов.
Рассмотрен порядок аналитического и
графического определения передаточных
отношений планетарных передач.
Представлены методики оптимального
выбора чисел зубьев колес наиболее
распространенных видов планетарных
механизмов, а также рассмотрены примеры
синтеза.
Методические
рекомендации предназначены для
выполнения раздела «Синтез зубчатых
механизмов» курсового проекта по теории
механизмов и машин.
Табл. 1. Ил. 9.
Библиогр.: 3 назв.
Рецензент
В.Н.Шевякин, проф., докт. техн. наук
Редактор Е.А.
Припачкина
Лицензия на
издательскую деятельность ЛР №020280 от
09.12.96.
Подписано
в печать с оригинал-макета . Формат
60841/16.
Усл. печ. л. 1.37.
Уч.-изд. л. 1.47. Тираж 100 экз. Заказ .
Подразделение
оперативной полиграфии Курского
государственного технического
университета.
Адрес университета
и подразделения оперативной полиграфии:
305040, Курск, ул. 50
лет Октября, 94.
1. Структурные
схемы планетарных зубчатых передач .
. . . . . . . . . . . . . . 4
2. Аналитическое
определение передаточного отношения
планетарного
механизма . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . 6
3. Методика выбора
чисел зубьев колес . . . . . . . . . . . . . . . . .
. . . . . . . . . . . 7
3.1. Редуктор Джемса
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . 8
3.2. Редуктор со
сдвоенными сателлитами . . . . . . . . . . . .
. . . . . . . . . . .10
3.3. Редуктор Давида
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . 11
3.4. Редуктор с
двумя внутренними зацеплениями . . . . .
. . . . . . . . . . . 12
3.5. Основные выводы
и рекомендации . . . . . . . . . . . . . . . . . . . .
. . . . . 16
4. Графический
метод определения передаточного
отношения
планетарной
передачи . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . 17
5. Методика
выполнения курсового проекта . . . . . .
. . . . . . . . . . . . . . . . . 19
Библиографический
список . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . 22
Планетарной
зубчатой передачей
называют механизм для передачи и
преобразования вращательного движения,
содержащий зубчатые колеса с перемещающейся
в пространстве осью вращения хотя бы
одного из них. Основными звеньями
планетарной зубчатой передачи являются
(рис.1): зубчатые колеса: солнечное - 1,
сателлиты – 2, корончатое – 3, а также
водило Н - звено, в котором установлены
оси сателлитов. Ось ОН
вращения водила Н, совпадающая с осью
О1
центральных колес, является основной
осью механизма.
Рис.1 Схема
планетарного механизма
При вращении
солнечного колеса 1 сателлиты 2 будут
обкатываться по нему и по корончатому
колесу 3, совершая плоское движение.
Перемещение осей сателлитов 2 приводит
к вращению водила Н, которое является
выходным звеном данного зубчатого
механизма.
Планетарные
механизмы обладают ценными свойствами:
они имеют меньшие радиальные габариты
и массу, работают с меньшим шумом, чем
соответствующие зубчатые передачи с
неподвижными осями; удобны в сборке и
надежны в работе. Основным преимуществом
планетарных передач является возможность
осуществлять большие передаточные
отношения при сравнительно небольших
габаритах и высоком к.п.д. Поэтому они
получили весьма широкое распространение,
найдя применение в приводах транспортных
машин, станков, в металлургическом и
текстильном оборудовании, в гусеничных
машинах, автомобилях, в авиации, в
приводах многих машинных агрегатов и
в разнообразных приборах. Однако надо
иметь в виду, что планетарные механизмы
имеют более сложную конструкцию, требуют
повышенной точности изготовления.
При степени
подвижности планетарного механизма
W=1
он называется собственно планетарным,
а при W≥2-дифференциальным.
Степень подвижности механизма,
изображенного на рис.1, равна W=35-24-6=1.
Простейшие
кинематические схемы планетарных
передач показаны на рис.2 и рис.3.
а)
б)
Рис.
2. Схемы планетарных зубчатых передач:
б) редуктор со
сдвоенными сателлитами
В курсовом
проектировании по теории механизмов
и машин решаются задачи определения
чисел зубьев колес планетарных зубчатых
передач по заданному передаточному
отношению Uпл.
В зависимости от величины Uпл
сначала выбирается одна из схем,
показанных на рис.2 или рис.3 с учётом
рекомендаций (cм.табл.1.).
При этом должны быть обеспечены
минимальные радиальные размеры колес
передачи и заданное передаточное
отношение с достаточной точностью Uпл
± 3 %, а также
условия работоспособности и сборки.
Следовательно,
для возможности правильного назначения
чисел зубьев всех колес планетарной
передачи и обеспечения требуемого
передаточного отношения необходимо
иметь выражение для определения
передаточного отношения Uпл
для каждой
выбранной схемы.
а)
б)
Рис. 3. Схемы
планетарных зубчатых механизмов:
а) редуктор Давида;
б) редуктор со
сдвоенными сателлитами и двумя
внутренними
зацеплениями
Рассмотрим порядок
получения формулы для расчета
передаточного отношения планетарного
механизма через известные числа зубьев
его колес на примере редуктора Джемса
(рис.1) или (рис.2,а).
Входным звеном в
этом механизме является солнечное
колесо 1, а выходным - водило Н.
Тогда искомым
является выражение
где обозначение
Для определения
передаточного отношения планетарного
механизма используется метод обращения
движения или метод остановки (“фиксации”)
водила.
Для реализации
этого метода всем звеньям механизма
сообщается дополнительное воображаемое
вращательное движение вокруг центральной
оси О1Он
с угловой скоростью (- н).
Тогда получим новый - обращенный
механизм, который будет примечателен
тем, что его звено Н , бывшее ранее
водилом, станет неподвижным. Следовательно,
неподвижным станет и центр О2,
т.е. обращенный механизм будет представлять
собой обычную зубчатую передачу с
неподвижными осями вращения колес. При
этом угловые скорости звеньев нового
обращенного механизма будут равны:
- солнечного колеса
1 - 1
=1-н;
- корончатого
колеса 3 - 3=0-н=-н;
- водила Н -
н=н-н=0.
Таким образом,
при остановленном водиле ведомым звеном
становится корончатое колесо 3, и
передаточное отношение обращенного
механизма будет равно
Следовательно,
искомое передаточное отношение
планетарного механизма
где U(н)13-
является передаточным отношением
обычной зубчатой передачи с неподвижными
осями, для которой по формуле Виллиса:
Тогда, подставляя
полученное значение, имеем для
планетарного механизма редуктора
Джемсa:
Аналогично можно
вывести формулы для определения
передаточных отношений механизмов,
изображенных на рис.2.б, рис.3, а и б:
- для схемы на
рис.2.б:
- для схемы на
рис.3.а:
- для схемы на
рис.3.б:
При назначении
чисел зубьев колес планетарной передачи
необходимо
учитывать ряд требований и условий,
важнейшие из которых следующие.
1. Числа зубьев
Z1,
Z2…
должны быть целыми числами.
2. Сочетание чисел
зубьев колес должно обеспечивать
требуемое передаточное отношение Uпл
с допустимой
точностью ±3 % .
3. При отсутствии
специальных требований желательно
использовать в передаче нулевые колеса.
Это ограничение записывают в форме
отсутствия подреза зубьев: для колес
с внешними зубьями, нарезанными
стандартным инструментом, Zi
≥ Zmin=17;
для колес с внутренними зубьями – Zi
≥ Zmin=85.
4. Оси центральных
колес и водила Н планетарной передачи
должны лежать на одной прямой для
обеспечения движения точек по соосным
окружностям (условие
соосности ).
5. При расположении
сателлитов в одной плоскости, т. е. без
смещения в осевом направлении, соседние
сателлиты должны быть расположены так,
чтобы между окружностями вершин
обеспечивался гарантированный зазор
(условие
соседства)
:
(
Z1+Z2)sin
>Z2+2,
(3.1)
где k
– число сателлитов.
6. Сборка нескольких
сателлитов должна осуществляться без
натягов так, чтобы зубья всех сателлитов
одновременно вошли во впадины солнечного
и корончатого колес:
где Z1-
число зубьев центрального колеса,
k-число
сателлитов, р - число оборотов водила,
Сo-целое
число.
Рассмотрим порядок
синтеза планетарных механизмов,
представленных на рис. 2 и рис. 3.
Составим четыре
основные уравнения проектирования.
2. Условие
соосности
состоит в
том, чтобы оси солнечного, корончатого
колёс, а также водила лежали на одной
прямой. Для этого должна выполняться
следующая размерная цепь:
d3=d1+2d2;
(3.4)
откуда
mZ3=mZ1+2mZ2;
(3.5)
сокращая на m,
получаем
Z3=Z1+2Z2
или Z3
- Z2
= Z1
+ Z2
. (3.6)
3. Условие
сборки
состоит в том, чтобы зубья всех сателлитов
одновременно вошли при сборке во впадины
и солнечного колеса, и корончатого
колеса:
где k - число
сателлитов;
С - целое число.
Для выполнения
этого условия необходимо, чтобы
расстояние О2О2
между центрами двух соседних сателлитов
было больше суммы радиусов окружностей
вершин этих сателлитов:
O2O22ra2;
(3.8)
O2O2=2(r1+r2)sin
где к - число
сателлитов;
ra2=m
Тогда условие
соседства сателлитов будет иметь вид
(Z1+Z2)sin
Для подбора чисел
зубьев проектируемой планетарной
передачи необходимо решить совместно
все 4 уравнения. Необходимо также
учитывать, чтобы Zi17
для устранения подрезания.
Пример 1.
Исходные данные:
Uпл=4,8;
к3,
m=4 (мм).
1. Рассчитываем
вспомогательную величину
В=Z1+Z3=215
- 38 Uпл+3,25Uпл2=107,48.
Полученную до
ближайшего величину округляем большего
четного значения, кратного числу
сателлитов.
Принимаем В = 108.
2.Рассчитываем из
уравнения
Принимаем Z1
= 23.
3. Рассчитываем
Z3=B
-Z1=108-23=85;
Z385.
Принимаем Z3=85.
4. Рассчитываем
5. Рассчитываем
фактическое передаточное отношение и
сравниваем его с заданным
Uпл.факт.=1+
=
Отклонение
передаточного отношения спроектированной
планетарной передачи от заданного не
превышает 3 %, что допустимо.
6. Определим
максимально возможное количество
сателлитов из условия соседства
сателлитов:
k
Следовательно
Кmax=4.
Принятое значение
В=108 кратно 4, поэтому можно использовать
4 сателлита, и при этом условие сборки
не нарушится.
7. Рассчитываем
диаметры начальных (делительных)
окружностей колес:
d1=Z1m
=234=92
(мм);
d2=Z2m=314
=124 (мм);
d3=Z3m=854=340
(мм).
Таким образом,
задача геометрического синтеза
планетарного механизма решена.
Передаточное
отношение такой передачи при ведомом
водиле Н определяется по формуле
Условие соосности
с учетом того, что модуль всех колес
одинаковый, и колеса нарезаны без
смещения, имеют вид:
Z1+Z2=Z4-Z3.
(3.12)
Для обеспечения
больших передаточных отношений
Таким образом,
передаточное отношение
Тогда число зубьев
колеса 2 равно
Z2=Z1(Z2/Z1).
(3.15)
При условии Z3=Z1
число зубьев колеса 4 определится из
(3.12).Принимая максимальное значение
отношения Z2/Z1=3,
получим для схемы, показанной на рис.2.б:
Umах=1+(Z2/Z1)2+2Z2/Z1=1+9+23=16.
Обычно для такой
схемы принимают Uпл=6…12.
Определим минимальные числа зубьев
колёс передачи из условия Z3=20
и Z4=85.
Из (3.12) получим: Z4=Z1+Z2+Z3=Z1+Z2+20=85
или Z1+Z2=85-20=65.
Разделив обе части
полученного равенства на Z1,
получим: 1+(Z2/Z1)=65/Z1.
Подставив сюда
Z2/Z1
из (3.14), найдём зависимость
Z1=
65/
Зная величину
отношения Z2/Z1,
из (3.15) можно найти
Z2=Z1(Z2/Z1).
(3.17)
Число зубьев
колеса 3 найдём по формуле (3.12), приняв
Z1=Z3.
Максимально
возможное число сателлитов k можно
определить по формуле, полученной при
подстановке в (3.1) Z1
и Z2
из (3.14) и (3.16) соответственно:
k=
/arcsin[1,0308-(1/
Условие сборки,
обеспечивающее установку сателлитов
через равные углы, проверяется с помощью
формулы (3.2.).
Пример 2.
Определить числа зубьев колес передачи,
схема которой показана на рис.2.б, при
1. Из (3.16) найдем
Z1=65/
2. С помощью (3.14)
определим величину отношения Z2/Z1:
Z2/Z1=
Тогда число зубьев
сателлита 2 найдем по формуле (3.17):
Z2=(Z2/Z1)Z1=2.31662=46.33.
Принимаем
Z2=46.
3. Число зубьев
колеса 3 найдем из условия соосности
(3.12):
Z4=Z1+Z2+Z3=20+46+20=86.
4. Проверим величину
передаточного отношения при найденных
числах зубьев:
Расхождение с
заданным U
составляет менее 1%, что допустимо.
Условие сборки
выполняется уже при p
=1 оборота водила, что составляет 4800:
6. Проверим
выполнение условия соседства сателлитов,
найдя максимально допустимое число
сателлитов по формуле (3.18):
kmax
= /arcsin
(1,0308-1/) = 3,14/ arcsin(
1,0308-1/
Схема редуктора
показана на рис.3,а. Это так называемый
редуктор Давида. При неподвижном
солнечном колесе 1 с числом зубьев Z1
и ведущем водиле Н передаточное отношение
определится по формуле :
Из (3.19) видно, что
наибольшему передаточному отношению
соответствует наименьшая разность
Z1Z3
- Z2Z4.
Это возможно при Z4=Z1-1
и Z2=Z3-1.
Принимая Z3=Z1
и Z2=Z4,
получим
Отсюда видно, что
Z1≡2
т.е. оптимальное
число зубьев солнечного колеса Z1
для рассматриваемой схемы равно
удвоенному передаточному отношению.
Решая (3.20)
относительно Z1,
как квадратное уравнение, можно получить
точное значение минимального числа
зубьев солнечного колеса
Z1=
Числа зубьев колес
2, 3 и 4 определятся следующим образом:
Z4=Z1-1;
Z3=Z1;
Z2=Z3-1.
Используя
зависимость (3.20), найдем диапазон
возможных
значений
Максимальное
число сателлитов в этом случае kmax=5
при любом значении
Пример 3.
Определим числа зубьев планетарной
передачи с двумя внешними зацеплениями
при передаточном отношении
1. Из (3.21) найдем
число зубьев Z1=2U=32.
Принимаем Z3=Z1=32.
2.Число зубьев
ведомого колеса Z4=Z1-1=32-1=31.
3.Число зубьев
колеса 2 блока сателлитов: Z2=Z4=31.
4.Определим
передаточное отношение при найденных
числах зубьев
Отклонение от
заданного
Передаточное
отношение такого редуктора определяется
по формуле:
Найдем зависимость
чисел зубьев Z1
и Z4
от
Минимальное число
зубьев колес с внутренними зубьями
равно 85, а находящихся в зацеплении с
ними сателлитов равно 20.
Минимальная
разность чисел зубьев колес, находящихся
во внутреннем зацеплении, равно 8.
Обозначим разности чисел зубьев Z1-Z2=D
и
Z4-Z1=C.
Тогда Z2=Z1-D
и Z3=Z4-D.
После подстановки в (3.22) величин Z2
и Z3
получим:
откуда
D
=
Здесь
Минимальное
передаточное отношение при Z2=20
из (3.23) получается равным 26,5 , а максимальное
при D=8
равно 828.
Задаваясь разностью
С=Z4-Z1
в пределах от 1 до 4, можно при известном
передаточном отношении
Z2=Z1-D,
(3.24)
Z3=Z2+C=Z1-D+C,
(3.25)
Z4=Z1+C.
(3.26)
Если при этом
получится Z2<20,
то нужно увеличить С. Для предотвращения
многовариантных расчетов можно
воспользоваться графиком (рис.4),
построенным по результатам вычислений
при различных числах зубьев сателлитов
Z2
с использованием (3.23) при передаточных
отношениях
Число зубьев
сателлита Z2
и разность С должны быть выбраны по
возможности наименьшими, т.к. при этом,
во-первых, уменьшается масса колес
передачи и, во-вторых, появляется
возможность создания многосателлитной
передачи. Так, например, при U=30
целесообразно принять С=1 и с помощью
графика найти Z2=22.
Тогда при Z1=85
получим Z3=22+1=23
и Z4=85+1=86.
Передаточное отношения при таких числах
зубьев составит величину
Рис.4. Выбор числа
зубьев Z2
для различных
значений Uпл=10…70
и С=1…4
Количество
сателлитов можно определить из условия
соседства сателлитов второго ряда
колес передачи (рис.5), т.е. исходя из
чисел зубьев Z3
и Z4,
т.к. Z4>Z2.
В соответствии
со схемой зацепления, показанной на
рис.5, условие соседства сателлитов
примет вид:
где k-
число сателлитов.
sin
> –1, (3.28) откуда
можно найти максимальное количество
сателлитов
kmax=
= . (3.29)
Рис .5. К определению
условия соседства сателлитов
На рис.6. представлены
результаты расчета максимального числа
сателлитов по формуле ( 3.29 ) для передач
с
Рис.6. Выбор
максимального числа сателлитов для
различных
значений Uпл=10…70
и С=1…4
Планетарные
редукторы четырех рассмотренных типов
могут быть просто и достаточно оптимально
синтезированы по изложенной выше
методике.
Все рекомендации
по проектированию планетарных передач
сведены в табл.1, которая является
алгоритмом выбора типа передачи и
определения чисел зубьев всех колес
редуктора.
Планетарные
передачи с двумя внешними зацеплениями
(рис.3,а) имеют слишком большие радиальные
размеры и низкий к.п.д. и как силовые
применяются редко.
Число сателлитов
можно выбрать с помощью рис.4 или
определить их максимально допустимое
количество с помощью формул (3.10), (3.18)
или (3.29).
В основу метода
графического определения передаточного
отношения планетарной передачи положен
треугольный закон распределения
окружных скоростей точек вращающегося
звена Еcли
известна скорость VА
точки А (см. рис.7) звена ОА, вращающегося
относительно неподвижного шарнира О
с угловой скоростью ω, то скорости
остальных точек звена определяются
прямой, соединяющей точку О и конец
вектора
Для пары зубчатых
колес, имеющих начальные радиусы rw1
и rw2
, передаточное
отношение определится как
Рис.7.
рис.8.
Так как окружные
скорости зацепляющихся колес на
начальных окружностях одинаковы
(рис.8), то можно написать
V=
ω1rw1
= ω2rw2
или ω1=
V/rw1
и ω2
= V/rw2.
Поэтому можно
найти тангенсы углов 1
и 2
, образованных линиями распределения
скоростей колес и осью, соединяющей
центры О1
и О2:
tg1=
= ω1
и tg2=
= ω2
. (4.2)
Таким образом,
величину передаточного отношения можно
выразить и через отношение тангенсов
углов 1
и 2,
подставив их в (4.1):
U=
(4.3)
Полученные
зависимости используются для графического
определения передаточного отношения
зубчатых механизмов с подвижными осями
колес.
Рассмотрим пример
графического определения передаточного
отношения планетарного механизма
редуктора Джемса (рис.9).
Спроектируем на
вспомогательную вертикаль точки О1,
О2, П1и П2(рис.9,б и в).
Зададимся произвольной величиной
скорости
через
отношение длин отрезков “ав” и “ас”,
олицетворяющих скорости точек входного
и выходного звеньев на одинаковом
расстоянии от оси вращения.
а)
б) в)
Рис .9.Графическое
определение передаточного отношения
планетарной
передачи
Построенные
линии ЭпV1
и ЭпVН
распределения скоростей для солнечного
колеса и водила соответственно определяют
величины углов 1
и н
для ведущего и ведомого звеньев. Тогда
величина передаточного отношения может
быть определена отношениями
В
данном примере величина
Проектирование
планетарного редуктора является
заключительным этапом в ходе выполнения
курсового проекта по ТММ по разделу
«Зубчатые передачи». Исходными данными
являются передаточное отношение
планетарной передачи и модуль.
Передаточное отношение Uпл
либо задается, либо вычисляется по
формуле:
UПЛ
=
где
nДВ
- число об/мин вала электродвигателя
проектируемой или исследуемой машины;
N-
число об/мин главного вала машины,
равное числу рабочих ходов в минуту
исполнительного звена машины;
UР=Z2/Z1-передаточное
число рядовой ступени, геометрический
синтез которой выполняется в ходе
курсового проектирования.
Проектирование
планетарной передачи выполняется в
следующей последовательности:
1.
По величине передаточного отношения
UПЛ
выбирается схема планетарного редуктора
(рис.2 или рис.3) в соответствии с
рекомендациями табл.1.
2. Для выбранной
схемы механизма определяются числа
зубьев всех колес с учетом обеспечения
условий соосности, соседства сателлитов
и сборки.
3.
Найденные числа зубьев подставляются
в формулу для определения передаточного
отношения, и вычисляется фактическая
величина UПЛ.
Расхождение с заданной величиной не
должно превышать ± 3 % .
4.
Определяются делительные диаметры
колес передачи d=mz
из расчета, что все колеса имеют
одинаковый модуль m
и нарезаны без смещения.
5.
На листе курсового проекта с общим
названием «Синтез зубчатых механизмов»
вычерчивается схема планетарного
механизма в выбранном масштабе в двух
проекциях (см. рис. 9,а и б). На схеме
должны быть показаны делительные
окружности всех колес с указанием их
диаметров и водило. Водило изображается
условно в виде крестовины с шириной
радиальных участков В=10мм вне зависимости
от масштаба изображения. Крестовина
вычерчивается основными линиями.
Вращательные кинематические пары
шарниров О1
и О2
вычерчиваются в виде окружностей
диаметром 3 мм.
6.
Строится картина распределения скоростей
звеньев планетарной передачи (рис.9,в).
Исходный вектор
7.
По результатам построения определяется
передаточное отношение по формулам
(4.4) и (4.5). Расхождение величин UПЛ,
полученных аналитически и графически,
не должно превышать 2 %.
8. Оформить раздел
«Синтез планетарной передачи» в
расчетно-пояснительной записке, где
приводятся обоснование выбора схемы,
расчет чисел зубьев, проверка условий
соосности, соседства и сборки, а также
проверка обеспечения заданного
передаточного отношения.
Сводная таблица
рекомендаций по проектированию
планетарной
передачи
Табл.1. Схема пере- дачи Диапазон
передаточных
отношений Формулы
для
определения
UПЛ Рекомендации
по определению чисел
зубьев колес передачи и
числа сателлитов
Рис.2,а
=2,9…6
Z1+Z3=215-38UПЛ+3,25UПЛ2
-округлить
до ближайшего четного, кратного числу
сателлитов; Z1=(Z1
+Z3)/UПЛ; Z3=(Z1
+Z3)
- Z1; Z2=(
Z3
- Z1)/2; kmax=/arcsin(1,047-2,047/UПЛ).
Рис.2,б
Z1=
Z3=65/ Z2/
Z1= Z2=
Z1(Z2
/Z1)-округлить; Z4=
Z1+
Z2+
Z3; kmax/arcsin(1,0308-1/
Рис.3,а
=12…30 Z1=
2UПЛ
- округлить; Z3=Z1;
Z2=
Z3-1; Z4=Z2;
kmax=5.
Рис.3,б
=26..100
Z1=85…87; C=1,2,3
или 4; D
= Z2=
Z1-D;
Z3=
Z2+C;
Z4=
Z1+C;
Библиографический
список
Теория механизмов
и машин. Под ред. В.А.Гавриленко.- М.:
Высш. шк. 1973.
2. Попов С.А.
Курсовое проектирование по теории
механизмов и машин. Под ред. К.В.
Фролова.-М.: Высш. шк., 1986.- 295с.
3. Юдин В.А., Барсов
Г.А., Чупин Ю.Н. Сборник задач по теории
механизмов и машин. М.: Высш. шк., 1982.

Оглавление
Структурные схемы планетарных зубчатых передач


А) редуктор Джемса;

2. Аналитическое определение передаточного отношения планетарного механизма
![]() =
=![]() =?,
(2.1)
=?,
(2.1)![]() читается как “передаточное отношение
от 1-го колеса к водилу Н при неподвижном
3-м колесе”.
читается как “передаточное отношение
от 1-го колеса к водилу Н при неподвижном
3-м колесе”.![]() =
=![]() 1-
1-![]() (2.2)
(2.2)![]() будет равно:
будет равно:![]() =1-
=1-![]() (2.3)
(2.3)![]() (2.4)
(2.4)![]() =1+
=1+![]() .
(2.5)
.
(2.5)![]() =1+
; (2.6)
=1+
; (2.6)![]() ;
(2.7)
;
(2.7)![]() =
. (2.8)
=
. (2.8)
Методика выбора чисел зубьев колес
![]() ,
(3.2)
,
(3.2)3.1. Редуктор Джемса (рис. 2,а)
1.Уравнение передаточного отношения
![]() =1+
=1+![]() (3.3)
(3.3)![]() (3.7)
(3.7)4. Условие соседства сателлитов.
![]() ;
(3.9)
;
(3.9)![]() (3.9)
(3.9)![]()
![]() Z2+2. (3.10)
Z2+2. (3.10)![]()
![]() число зубьев солнечного колеса
число зубьев солнечного колеса
![]() 17.
17.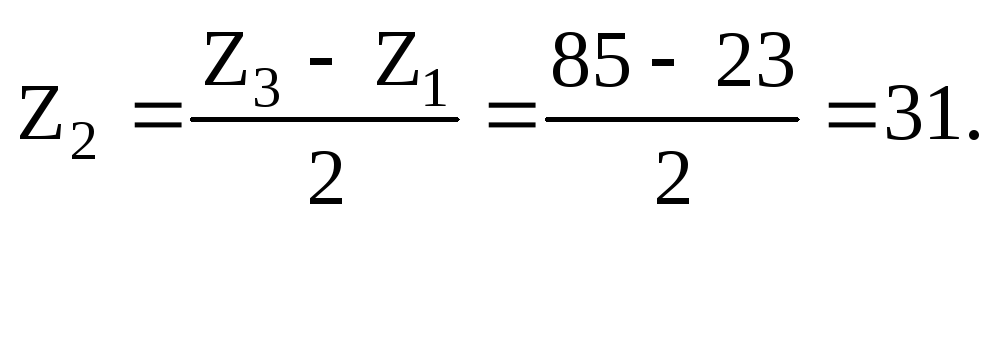
![]()
![]() 3%
3% .
.3.2 Редуктор со сдвоенными сателлитами (рис.2,б)
![]() = 1+ .
(3.11)
= 1+ .
(3.11)![]() произведение Z1Z3
должно быть минимальным, т.е. сами
величины Z1
и Z3
должны быть наименьшими. При этом Z1
= Z3
= Zmin=20.
Тогда условие соосности для такой
передачи примет вид Z4=Z2+2Z1.
Подставив это выражение в (3.11), получим:
произведение Z1Z3
должно быть минимальным, т.е. сами
величины Z1
и Z3
должны быть наименьшими. При этом Z1
= Z3
= Zmin=20.
Тогда условие соосности для такой
передачи примет вид Z4=Z2+2Z1.
Подставив это выражение в (3.11), получим:
![]() =
1+ = 1+ .
(3.13)
=
1+ = 1+ .
(3.13) ![]() в данном случае зависит только от
отношения Z2/Z1.
Поэтому, решая (3.13), как квадратное
уравнение, относительно Z2/Z1,получим:
в данном случае зависит только от
отношения Z2/Z1.
Поэтому, решая (3.13), как квадратное
уравнение, относительно Z2/Z1,получим:![]() .
(3.14)
.
(3.14)![]() =65/Z1,
откуда получим формулу для определения
числа зубьев Z1
солнечного колеса 1:
=65/Z1,
откуда получим формулу для определения
числа зубьев Z1
солнечного колеса 1:![]() .
(3.16)
.
(3.16)![]() )]
(3.18)
)]
(3.18)![]() =11.0
и числе сателлитов k=3.
=11.0
и числе сателлитов k=3.![]() =65/
=19,59. ПринимаемZ1=Z3=20.
=65/
=19,59. ПринимаемZ1=Z3=20.![]() -1=-1=2,3166.
-1=-1=2,3166.![]() =
1+ =1+
=
1+ =1+![]() =10,89.
=10,89.![]() =
= =Со
.
=Со
.![]() ) = 3,85 , что больше принятого k=3. Условие
выполняется.
) = 3,85 , что больше принятого k=3. Условие
выполняется.3.3. Редуктор с двумя внешними зацеплениями (редуктор Давида)
![]() =
, (3.19)
=
, (3.19)![]() =
=

![]() =
= = . (3.20)
= . (3.20)![]() (3.21)
(3.21)![]() +
+![]() .
.![]() .
При Z1=Zmin=17
величина
.
При Z1=Zmin=17
величина
![]() min=8.76.
При Z1=100
величина
min=8.76.
При Z1=100
величина
![]() =50.25,
но при этом радиальные размеры передачи
становятся слишком большими, а к.п.д.
низким.
=50.25,
но при этом радиальные размеры передачи
становятся слишком большими, а к.п.д.
низким.![]() .
Условие сборки (3.2) выполняется при р =
- .
.
Условие сборки (3.2) выполняется при р =
- .![]() =16.
=16.![]() =
=
![]() =
=![]() =
-16,25.
=
-16,25.![]() составляет 1.6%, что допустимо.
составляет 1.6%, что допустимо.3.4. Редуктор с двумя внутренними зацеплениями (рис. 3.Б)
![]() =
. (3.22)
=
. (3.22)![]() при условии обеспечения минимальных
радиальных размеров (минимальных чисел
зубьев).
при условии обеспечения минимальных
радиальных размеров (минимальных чисел
зубьев).![]() =
, (3.23)
=
, (3.23)![]()
![]() .
.![]() – абсолютное значение передаточного
отношения.
– абсолютное значение передаточного
отношения.![]() найти D,
а затем и числа зубьев всех остальных
колес при Z1=85:
найти D,
а затем и числа зубьев всех остальных
колес при Z1=85:![]() =10…70.
=10…70.
![]() =8622/8622-8523=-30.03
что на 0.1% отличается от заданного
=8622/8622-8523=-30.03
что на 0.1% отличается от заданного![]() .
.
![]()
Подставив сюда z3 из (3.25) и z4 из (3.26) и несколько преобразуя, получим:

![]() =10…70
при разных значениях
с = 1…4. Как видно из анализа рис.6, с
увеличением передаточного отношения
=10…70
при разных значениях
с = 1…4. Как видно из анализа рис.6, с
увеличением передаточного отношения
![]() максимально возможное число сателлитов
уменьшается и, например, для
максимально возможное число сателлитов
уменьшается и, например, для
![]() =60
значение “C”
допускается только равным 1 и кmax
= 3, а для С
≥ 2 и
=60
значение “C”
допускается только равным 1 и кmax
= 3, а для С
≥ 2 и
![]() ≥ 40 возможен только один сателлит, и
водило превращается в кривошип.
≥ 40 возможен только один сателлит, и
водило превращается в кривошип. 
3.5. Основные выводы и рекомендации.
4. Графический метод определения передаточного отношения планетарной передачи
![]() .
.![]() =ω1/ω2.
(4.1)
=ω1/ω2.
(4.1)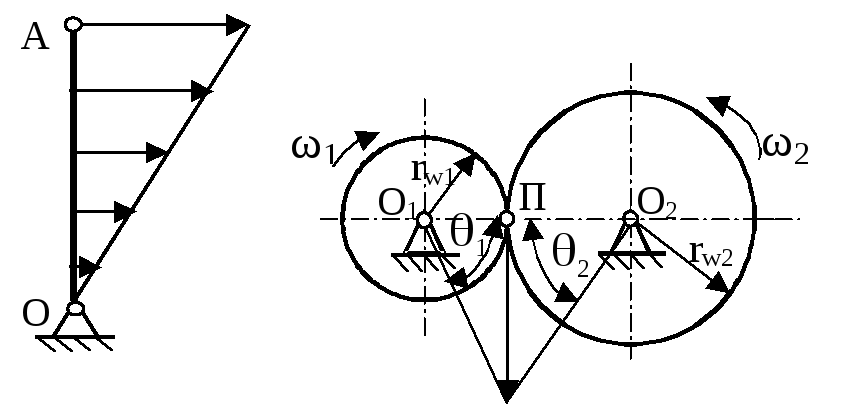
![]() =
=![]() точки,
являющейся осью вращения сателлита и
одновременно принадлежащей водилу Н.
Проведем линию распределения скоростей
ЭпVHдля точек водила, которая пройдет через
точку О1, и конец вектора
точки,
являющейся осью вращения сателлита и
одновременно принадлежащей водилу Н.
Проведем линию распределения скоростей
ЭпVHдля точек водила, которая пройдет через
точку О1, и конец вектора![]() .
Тогда линия ЭпV2распределения скоростей сателлита 2
пройдет через т.П2 и конец вектора
.
Тогда линия ЭпV2распределения скоростей сателлита 2
пройдет через т.П2 и конец вектора![]() .
Максимальную скоростьV2,
равную отрезку ‘ав’, будет иметь точка
П1 касания сателлитов и солнечного
колеса 1. Эпюра ЭпV1распределения скоростей солнечного
колеса 1 пройдет через т. О1и конец
вектора скоростиV1.
Таким образом, передаточное отношение
рассматриваемого планетарного механизма
можно рассчитать по формуле:
.
Максимальную скоростьV2,
равную отрезку ‘ав’, будет иметь точка
П1 касания сателлитов и солнечного
колеса 1. Эпюра ЭпV1распределения скоростей солнечного
колеса 1 пройдет через т. О1и конец
вектора скоростиV1.
Таким образом, передаточное отношение
рассматриваемого планетарного механизма
можно рассчитать по формуле:![]() = = /
= = /![]() =
=
![]() =
(4.4)
=
(4.4)
![]() =
= (4.5)
=
= (4.5)![]() является положительной, т. к. векторы
является положительной, т. к. векторы![]() и
и![]() направлены
в одну сторону.
направлены
в одну сторону.5. Методика выполнения курсового проекта
![]() ,
, ![]() скорости
точки О2
принимается произвольной длины (40…60
мм ). Наклонные линии распределения
скоростей проводятся тонкими линиями.
скорости
точки О2
принимается произвольной длины (40…60
мм ). Наклонные линии распределения
скоростей проводятся тонкими линиями.
![]() =
=
![]() =1+
=1+
![]() =6…12
=6…12
![]()
![]() –округлить
до ближайшего целого числа;
–округлить
до ближайшего целого числа;![]() - 1;
- 1;![]() ).
).
![]() =
=

![]() =
=
![]() =
=
![]() –округлить
до ближайшего целого;
–округлить
до ближайшего целого;  .
.
