Лекция 7. Элементы матричного анализа

7.1. Линейное пространство, базис, размерность

Определение. Множество элементов x₁, y₁, z₁ … любой природы называется линейным пространством, если выполнены следующие три требования:

1. Имеется правило, посредством которого любым двум элементам х и y множества ставится в соответствие третий элемент z этого множества, называемый

2. Имеется правило, посредством которого любому элементу х множества и любому действительному числу  ставится в соответствие элемент и этого множества, называемый

3. Указанные два правила подчинены следующим восьми аксиомам:

Замечание. При введении понятия линейного пространства абстрагируются не только от природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов и произведения элемента на число.

Элементы линейного пространства называются векторами.

Примеры линейных пространств:

Определение.

где - произвольные числа .

Определение. Элементы называются линейно зависимыми,

линейно независимыми называются

Свойства линейной зависимости и независимости:

1

2

3

4

Определение. Линейное пространство называется n-мерным,

n – называется

Обозначается dim R.

Определение. Система векторов в пространстве называется базисом, если:

(1)

Равенство (1) называется разложением вектора e по базису . Числа называются координатами вектора e в базисе .

Рассмотрим новый базис x₁, x₂ …. x_n. Каждый из векторов нового базиса может быть представлен линейной комбинацией векторов старого базиса:

Или в сокращенной записи

Линейная независимость векторов x₁, x₂ …. x_n равносильна линейной независимости строк матрицы

2. Линейные операторы, матричная запись

Рассмотрим два линейных пространства: размерности n и размерности m.

Определение. Если задан закон (правило), по которому каждому вектору пространства ставится в соответствие единственный вектор пространства , то говорят, что

1. Оператор (преобразование) называется линейным,

Вектор называется образом вектора ,

Вектор - прообразом вектора .

Замечание. Если пространства и совпадают, то оператор отображает пространство в себя и называется линейным преобразованием пространства . Далее мы будем рассматривать именно такие операторы.

Можно показать,

Матрица называется матрицей оператора

в базисе , а ранг r матрицы А – рангом оператора .

Определим нулевой оператор , переводящий все векторы пространства в нулевые векторы и тождественный оператор , действующий по правилу: .

2. Собственные числа и собственные векторы линейного

оператора

Определение. Вектор называется собственным вектором линейного оператора , если

(2)

Число  называется собственным значением оператора (матрицы А), соответствующим собственному вектору .

Замечание. Из определения следует, что собственный вектор под действием линейного оператора переходит в вектор, коллинеарный самому себе, т.е. просто умножается на некоторое число.

Равенство (2) можно записать в матричной форме:

или в развернутом виде

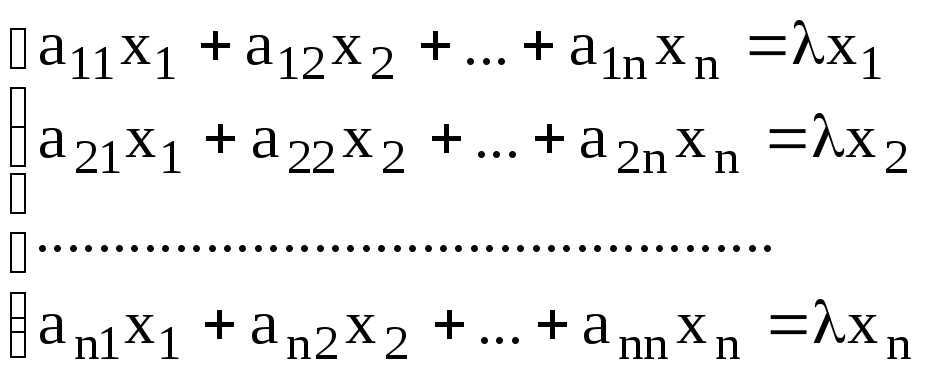
Преобразуем

.

Эта однородная система всегда имеет нулевое решение х=0=(0,0,…,0). Для существования ненулевого решения, согласно следствию из теоремы Крамера, необходимо и достаточно, чтобы определитель системы равнялся нулю

(3)

Определитель является многочленом n-ой степени относительно . Этот многочлен называется

Пример.

Наиболее простой вид принимает матрица А линейного оператора , имеющего n линейно независимых собственных векторов с собственными значениями, собственно равными . Векторы примем за базисные. Тогда матрица оператора в базисе, состоящем из его собственных векторов, является диагональной и имеет вид

Верно и обратное, если матрица А линейного оператора в некотором базисе является диагональной, то базис состоит из множества собственных векторов.