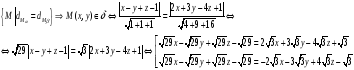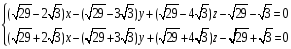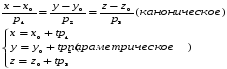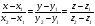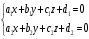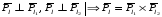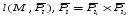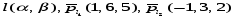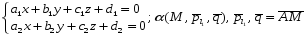Прямые и плоскости в пространсттве

Прямые и плоскости в пространстве.

§22 Различные способы задания плоскости в пространстве. Общий подход к решению задач на составление уравнений плоскости.

Плоскость в пространстве однозначно определяется заданием:

1. ее точки и нормального вектора перпендикулярного = α(М₀, )

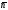2. ее точкой и двумя направляющими векторами(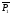не параллельно , P₁и P₂ параллельно α)= α(M₀, ,)

3. Тремя ее точками M₁,M₂,M₃=α(M₁,M₂,M₃₎

22.1 Уравнение плоскости заданное точкой и нормальным вектором.

α(М₀, 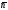) R(o,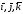) M₀(x₀,y₀,z₀) 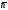(a,b,c)

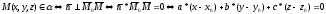(22,1)

(22,1)=> ax+by+cz+d=0, d=(-ax₀-by₀-cz₀) (22,2)

(22,2)- обще уравнение плоскости. Геометрический смысл коэффициентов, в котором, a, b и с состоит в том, что это и есть координаты.

Теорема (22.1)

Плоскость есть поверхность первого порядка.

Доказательство: действительно в пункте (22,1) мы доказали то уравнение плоскости имеет вид ax+by+cz+d=0, d=(-ax₀-by₀-cz₀).

Теорема(22.2)(О классификации плоскостей первого порядка)

Любое уравнение вида (22.2) в котором определяет плоскость.

Доказательство: Т.к. то уравнение(22.2) имеет один корень (x0,y0,z0). ax+by+cz+d=0(22,3). Вычитаем (22,3) из (22,2)=> 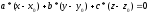А это и есть уравнение (22,1), которое определяет плоскость проходящую через

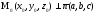
22.2 Уравнение плоскости, проходящей через M₀, ,.

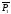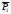α(M₀, 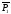,), M₀(x₀,y₀,z₀), (p₁,p₂,p₃),

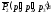
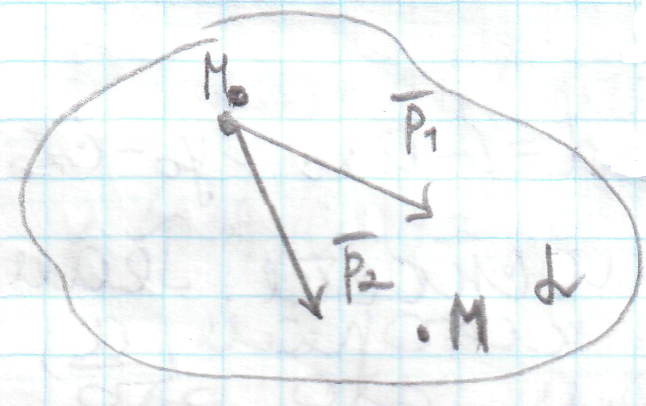
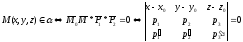(22,4)

22.3 Уравнение плоскости, проходящей через 3 точки.

α(M₁, M₂ , M₃), M₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂), M₃(x₃,y₃,z₃)

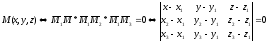(22,5)

Общий подход к решению задач: Плоскость.

1. Вычислите один из способов задания плоскости: 1) α(М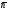₀, ) 2) α(M₀, 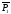,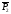) 3) α(M₁, M₂ , M₃₎

2. Запишите уравнение, соответствующее выбранному способу:

1)

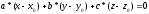
2)

3)

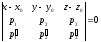
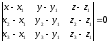
3. Запишите в общем виде.

ax+by+cz+d=0

Замечание: в решении задач на составление уравнений плоскостей, не всегда удается сразу найти способ задания плоскости, но часто для нее нахождение объектов, определяющих плоскость, помогают формулу вычисления расстояния от точки до плоскости и вычисление угла между плоскостями.

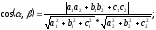
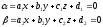
§23 Прямая линия в пространстве. Различные способы задания прямой в пространстве и ее уравнения. Общий подход к решению задач на составление уравнений прямых

Прямая в пространстве однозначно определяется заданием:

1. ее точки и направляющего вектора, l (М₀,)

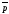2. двух ее точек, l (M₁,M₂)

3. двух плоскостей по которым она пересекается, l(α,β)

23.1 Уравнение прямой, заданной l (М₀,)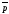

l (М₀,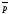), M₀(x₀,y₀,z₀), (p₁,p₂,p₃)

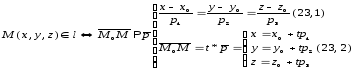
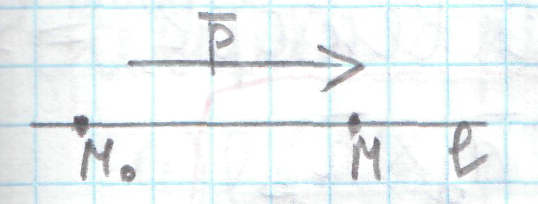
(23,1)-каноническое; (23,2)-параметрическое

23.2 Уравнение прямой, проходящей через М1, М2

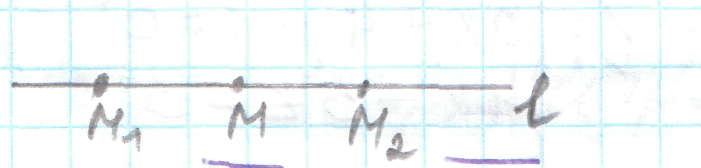
l (M₁,M₂)

23.3 Уравнение прямой заданной двумя плоскостями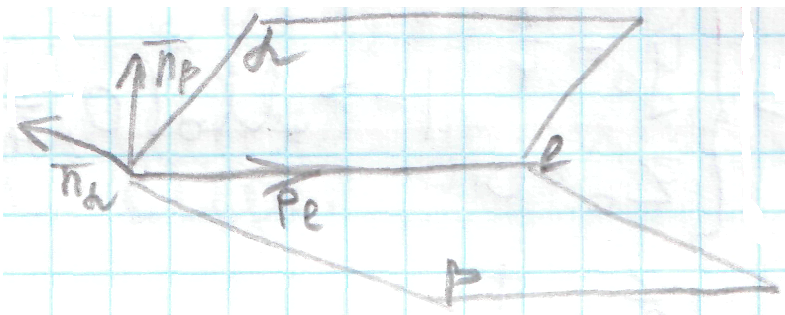

l(α,β), 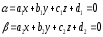(23,4) (23,4)- общее уравнение прямой

Рассмотрим переход от (23,4) к (23,1)

Пусть 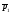- направляющий вектор l,

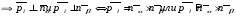
В качестве точки M₀(x₀,y₀,z₀) можно взять точку одну из координат у которой можно взять произвольно, а две другие найдутся как решение системы.

Пример:

l(α,β),

Пусть произвольная ;

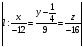
Общий подход к решению задач: Прямая.

1. Выделите один из трех способов задания прямой.

а) l (М₀,)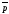

б) l (M1,M2)

в) l(α,β)

2. Запишите уравнение, соответствующее выбранному способу

1. 

2. 

3. 

3. Запишите уравнение в каноническом виде.

23.4 Вычисление расстояния от точки до прямой.

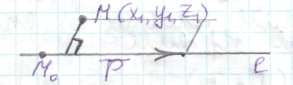
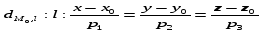
23.5 Вычисление расстояния между скрещивающимися прямыми

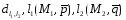
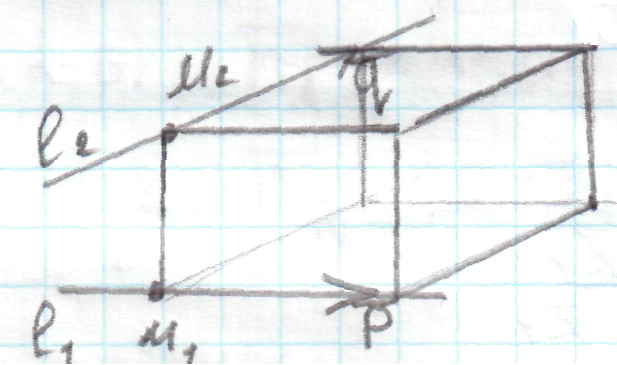
Параллелепипед:

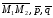
23.6 Нахождение угла

Пример: Составьте уравнение прямой

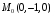
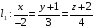
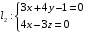
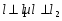
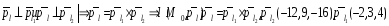
§24 Метод координат в решении геометрических задач

1. Через точку М(0,-1,1), провести прямую перпендикулярную прямой ,

1. 

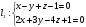
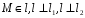
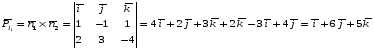
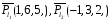
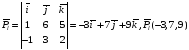
2) Записать уравнение

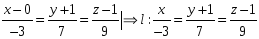
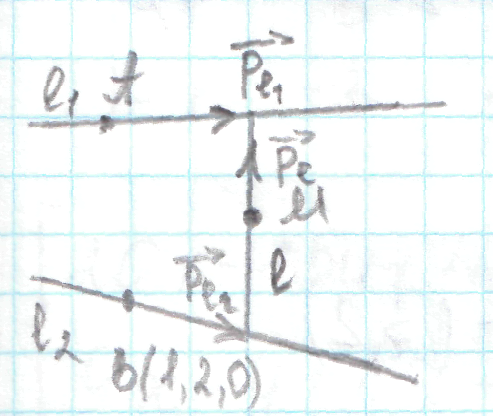
2. Составить уравнение прямой проходящей через М(0,-1,1) и пересекающие прямые l₁ и l_2.

,

1. 

2. 

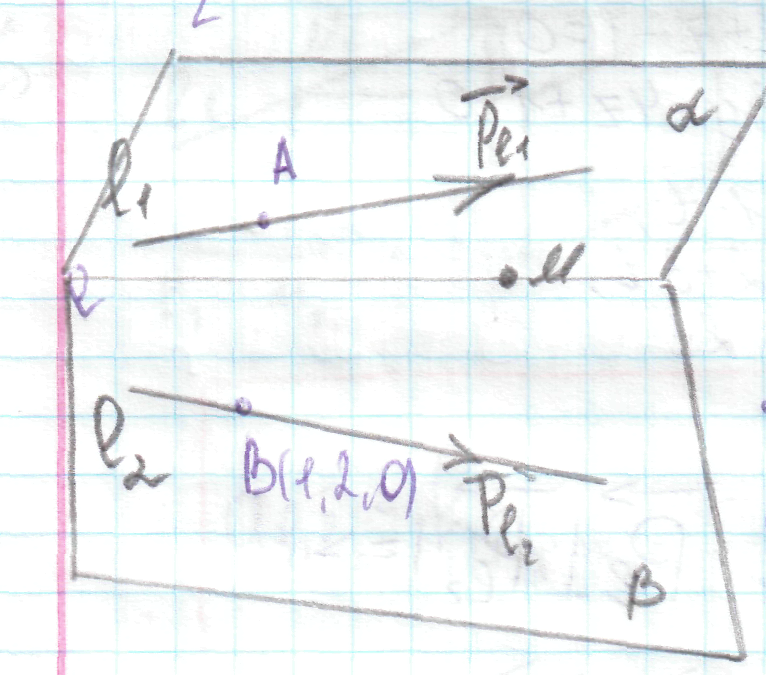
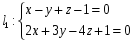
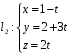
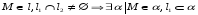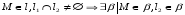
Пусть

3)

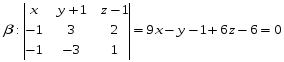
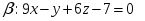
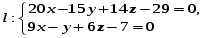
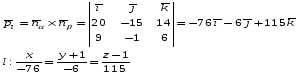
3. Составить уравнение прямой проходящей через М(0,-1,1), перпендикулярную l₁ и пересекающую l₂

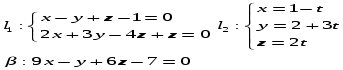
1)

l(α,β)

2) ,

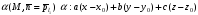3)

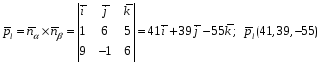
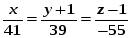
4. Даны две плоскости

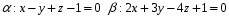
Составьте уравнение плоскостей, делящих двугранные углы этих плоскостей пополам.(Биссектриса плоскости)

Пусть δ- биссекторная плоскость, для α и β. δ= Г.М.Т.