1.9 Определение отношения теплоемкостей газа методом адиабатического расширения.

Цель работы: экспериментально определить показатель адиабаты _.

I. Теоретическое введение

Теплоемкостью(истинной)Cтела называется отношение элементарного количества тепла, сообщенного телу в каком-либо процессе, к соответствующему изменению температуры тела.

(1)

Удельной теплоемкостью с называется теплоемкость единицы массы однородного вещества:

(2)

где m — масса тела.

Молярной (мольной) теплоемкостью называется теплоемкость одного моля вещества:

, (3)

где - молярная масса вещества,-удельная теплоемкость

Выражение (1) справедливо для любого тела или системы, не зависимо от агрегатного состояния. В случае газов нагревание может происходить при постоянном объеме или при постоянном давлении

(4)

(5)

Если ν = 1 моль, то (4) И (5) определяют молярные теплоемкости.

Подставим в (4) первое начало термодинамики, учитывая, что V= const, тогда А=0:

(6)

Для изобарического процесса будем иметь

(7)

Подставим (7) в (5), получим

(8)

или

(9)

Запишем уравнение Менделеева-Клапейрона для одного моля

(10)

Продифференцируем его при условии, что Р= const:

(11)

Откуда

(12)

Подставим (12) в (9)

(13)

или

Для реальных газов чем выше давление газа, тем больше будет разность теплоемкостей отличатся отR.

Согласно распределению Максвелла-Больцмана для одного моля идеального газа имеем:

(14)

Откуда с учетом (6) получим

(15)

где i – число степеней свободы

Разделив (15) на (13) получаем теоретическое значение отношения теплоёмкости

(16)

что для двухатомных молекул (i = 5) дает ;

для одноатомных молекул (i = 3) ;

для молекул, состоящих из трех и более атомов (i = 6) .

II. Приборы и принадлежности

1.Закрытый стеклянный баллон с кранами.

2. Манометр

3. Ручной насос.

III. Описание экспериментальной установки и метода измерения

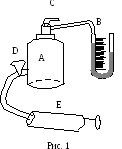
Экспериментальная установка состоит из стеклянного баллона А, соединенного с манометром В и с насосом Е. Посредством крана С, баллон А соединяется с атмосферой (рис. 1). Если при помощи насоса накачать в баллон некоторое количество воздуха то давление и температура внутри баллона повысятся. Вследствие теплообмена воздуха с окружающей средой через некоторое время температура воздуха, находящегося в баллоне сравняется с температурой внешней среды. Давление, установившееся в баллоне ,

где — атмосферное давление,

—добавочное давление по манометру, измеряемое разностью уровней жидкости в его коленах.

Если открыть на короткое время кран С, то воздух в баллоне будет расширяться. Если процесс происходит быстро, то его можно считать адиабатическим. Давление в сосуде установится равным атмосферному , а температура газа понизится до, а объём будет равен. В конце адиабатического процесса, в состоянии 2, параметры будут.

Применяя к 1 и 2 состояниям уравнение Пуассона, получим:

Или (17)

охладившийся при расширении воздух в баллоне через некоторое время вследствие теплообмена нагревается до температуры внешней среды ; давление возрастает до некоторой величины, где— новая разность уровней в манометре; объем воздуха не изменится и будет равен, то есть это состояние воздуха, которое назовем 3 состоянием, характеризуется параметрами. Так как в 1 и 3 состояниях воздух имеет одну и ту же температуру (процесс изотермический), то применяем закон Бойля-Мариотта.

(18)

Возведем обе части уравнения (18) в степень γ, получим:

(19)

Приравнивая, используя выражения (19) и (17), получим:

отсюда

Логарифмируя последнее выражение и учитывая, что: , получим:

тогда (20)

Таким образом, экспериментальное определение сводится к определениюи.