Погрешность суммы и разности приближенных чисел.

Теорема 1.1. Предельная абсолютная погрешность суммы нескольких приближенных чисел равна сумме предельных абсолютных погрешностей слагаемых.

Теорема 1.2. Предельная абсолютная погрешность разности приближенных чисел равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.

Таким образом, если ,, то,.

Примеры.

1. (Здесь и в последующих задачах будем считать, что даны приближенные числа, но в записи которых все цифры верные в широком смысле.)

;;.

2. ; ;..

Лекция 3.

«Погрешность произведения и частного приближенных чисел.

Погрешность возведения в степень и извлечения корня

из приближенных чисел.

Оценка погрешности результата вычислений по формуле.»

Погрешность произведения и частного приближенных чисел.

Теорема 1.3. Предельная относительная погрешность произведения нескольких приближенных чисел равна сумме предельных относительных погрешностей сомножителей.

Теорема 1.4. Предельная относительная погрешность частного от деления двух приближенных чисел равна сумме предельных относительных погрешностей делимого и делителя.

Таким образом, если ,, то,.

Пример.

Найдем относительную погрешность произведения двух приближенных чисел: ;. Из записи чисел определяем

; .

Значит, . Мы здесь брали число знаков с запасом в промежуточных результатах, но, округляя в большую сторону, и окончательный результат немного увеличили, чтобы сделать его более простым по записи.

Погрешность возведения в степень и извлечения корня из приближенных чисел.

Теорема 1.5. Предельная относительная погрешность степени приближенного числа равна произведению показателя степени на предельную относительную погрешность основания.

Теорема 1.6. Предельная относительная погрешность корня из приближенного числа равна предельной относительной погрешности подкоренного числа, деленной на показатель корня.

Таким образом, ,.

Пример.

Требуется найти относительную погрешность объема куба , гдеa– длина ребра, измеренная с погрешностью не более .

Предельная относительная погрешность .

Оценка погрешности результата вычислений по формуле.

В практике вычислений очень часто приходится оценивать погрешность числового значения величины, полученной в результате вычислений по формуле, которая содержит не одно, а несколько действий. Для оценки погрешности в этом случае следует последовательно применять теоремы о погрешностях.

Во всех задачах, рассмотренных в данном параграфе, будет задана формула, все составляющие которой – приближенные числа (за редким исключением), а найти нужно приближенный результат и записать его так, чтобы в записи все цифры были верными в широком смысле, а также надо определить абсолютную и относительную погрешности окончательного результата.

Примеры.

1. , где и вычислены приближенно с четырьмя верными значащими цифрами: ;.

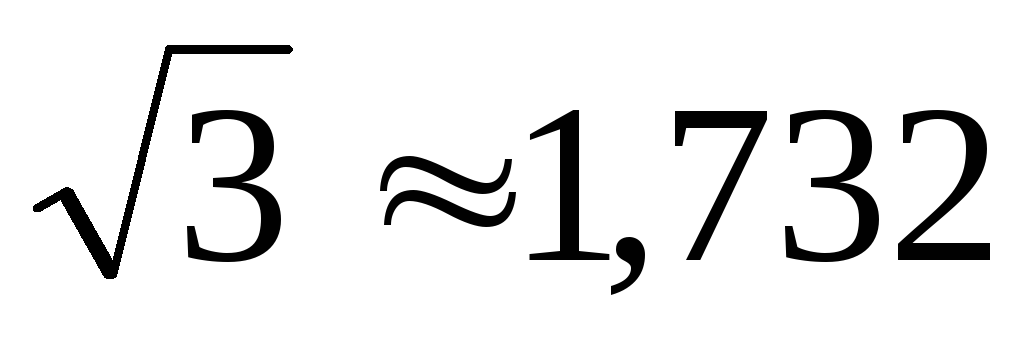Из записи числа определяем

; .

Значит,

. ,.

Мы округляли промежуточные результаты в сторону увеличения. Запишем ответ так, чтобы в записи все цифры были верные: . Действительно,

. .

Ответ: ,,.

2. , где .

; ;;. Округляя так, чтобы сохра­нить только верные цифры, получаем:. Действительно,.. Ответ:,,.

3. Вычисляют объем цилиндра по формуле . При этом принимают;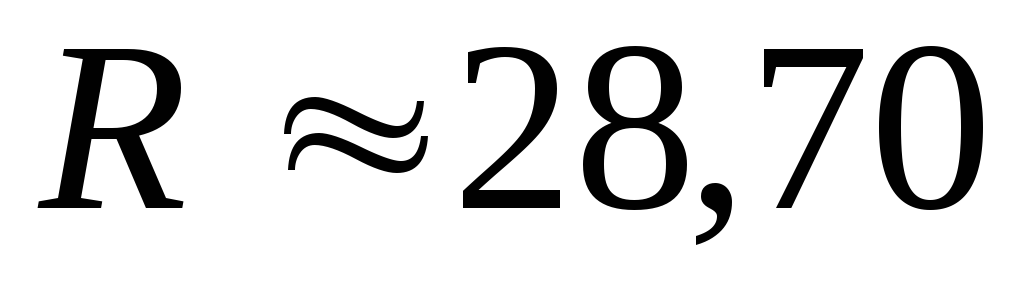см;см.

Так как в формуле участвует только умножение, то проще начать с оценки относительной погрешности. Из записи приближенных чисел видно:

, ,.

Отсюда получаем: .;. Округляя так, чтобы сохранить только верные цифры, получаем:. Действительно,

. .

Ответ: ,,.

4. Вычисляют период колебания маятника по формуле . При этом полагают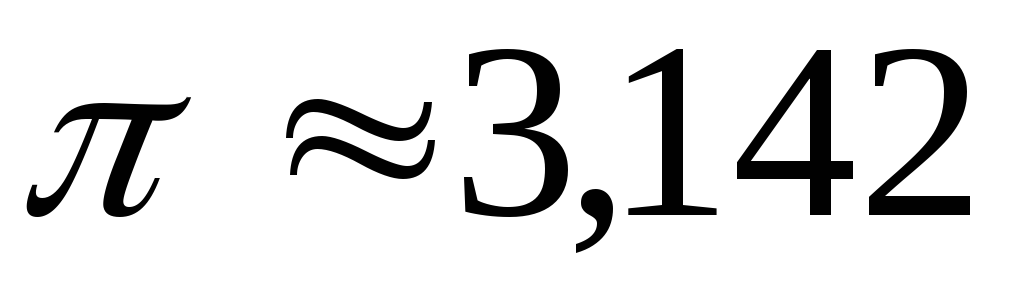;см;.

Из записи приближенных чисел видно: ,,. Отсюда получаем:

.

, .

Округляя так, чтобы сохранить только верные цифры, получаем: . Действительно,

. .

Ответ: ,,.

5. Вычислить , где;;;.

Здесь нужно произвести сложение, при котором легко определяется абсолютная погрешность, и, кроме того, умножение и деление, при которых легко определяется относительная погрешность. Поэтому при оценке погрешности надо будет переходить от одного вида погрешности к другому.

Найдем . Для дальнейшего придется найти относительную погрешность зна­менателя:. Теперь можем найти относительную погрешность искомого числаu.

.

, . Округляя так, чтобы сохранить только верные цифры, получаем:. Действительно,

.

Ответ: ,,.