Формула Симпсона.

Отрезок интегрирования разобьем на четное число элементарных отрезков равной длины точкамис шагом(). На каждом отрезкеподынтегральную функцию аппроксимируем многочленом второй степени, которая на этом отрезке имеет вид. Заметим, чтоi принимает здесь только нечетные значения от 1 до . Таким образом, подынтегральная функция аппроксимируется совокупностью квадратных многочленов или сплайном второй степени.

.

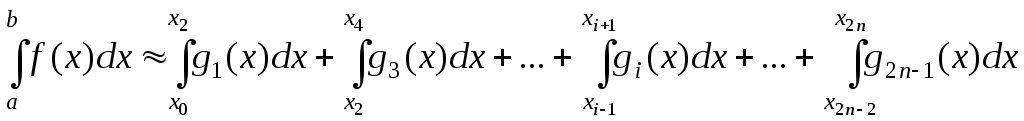Вычислим произвольный интеграл из правой части.

(5.1)

Коэффициенты ,имогут быть найдены из условия интерполяции, то есть из уравнений

,

,

.

Заметим, что точка является серединой отрезка, следовательно. Подставим это выражение во второе уравнение интерполяции:

.

Умножим это уравнение на 4 и сложим с остальными:

.

Последнее выражение в точности совпадает с выражением, стоящим в квадратных скобках формулы (5.1). Следовательно,

.

А значит,

.

Таким образом, формула Симпсона имеет вид:

.

Оценка погрешности квадратурных формул.

Оценим погрешность при использования метода средних прямоугольников в предположении, что функция бесконечно дифференцируема.

Разложим подынтегральную функцию в ряд Тейлора в окрестности точки,.

Тогда

Последний ряд содержит лишь нечетные степени x. Тогда

При малой величине шага h основной вклад в погрешность R будет вносить величина , называемая главным членом погрешностиR.

Применим метод средних прямоугольников к функции на отрезкес шагомh. Тогда

.

Итак, , где– постоянная величина. Погрешность в приближенном равенствеесть величина бесконечно малая высшего порядка по сравнению спри.

Степень шага h, которой пропорционален остаток R, называется порядком точности метода интегрирования. Метод средних прямоугольников имеет второй порядок точности.

Оценим погрешность при использовании метода трапеций также в предположении, что функция бесконечно дифференцируема.

Разложим подынтегральную функцию в ряд Тейлора в окрестности точки ().

Главный член погрешности R:

.

Применяя метод левых прямоугольников к функции на отрезкес шагомh, получаем

,

где

.

Итак, метод трапеций также имеет второй порядок точности.

Аналогично можно показать, что методы левых и правых прямоугольников имеют первый, метод Симпсона – четвертый порядок точности.

Лекция 17.

«Правило Рунге практической оценки погрешности.

Понятие об адаптивных алгоритмах.

Особые случаи численного интегрирования.

Метод ячеек. Вычисление кратных интегралов.»

Правило Рунге практической оценки погрешности.

Пусть некоторый метод интегрирования имеет порядок точности k, то есть , где– погрешность,A – коэффициент, зависящий от метода интегрирования и подынтегральной функции, h – шаг разбиения. Тогда

,

а при шаге

,

Выведенная формула называется первой формулой Рунге. Она имеет большое практическое значение. Если нужно вычислить интеграл с точностью , то мы должны вычислять приближенные значения интеграла, удваивая число элементарных отрезков, пока не добьемся выполнения неравенства

.

Тогда, пренебрегая бесконечно малыми величинами, можно считать, что

.

Если мы хотим получить более точное значение искомого интеграла, то за уточненное значение J мы можем принять вместо сумму

.

Это вторая формула Рунге. К сожалению, погрешность этого уточненного значения остается неопределенной, но обычно она на порядок выше, чем точность первоначального метода (когда за значение J мы принимаем ).

Для примера рассмотрим метод трапеций. Как было показано выше, порядок точности k этого метода равен 2.

,

где . По второй формуле Рунге

,

где есть приближенное значение интеграла найденное методом Симпсона с шагом. Так как порядок этого метода равен 4, то в данном примере применение второй формулы Рунге увеличило порядок точности на 2.