Вычисление значений многочленов.

Очень часто в качестве аппроксимирующей функции берут многочлен. Это связано с тем, что множество многочленов всюду плотно во множестве непрерывных функций. То есть имеет место следующая теорема.

Теорема 4.1. (Теорема Вейерштрасса.) Если , то для любогосуществует многочлентакой, чтопри всех.

Кроме того, и это немаловажно, значения многочлена легко вычисляются. Рассмотрим алгебраический многочлен

,

где ,, …,– числовые коэффициенты,n – степень многочлена. Если проводить вычисления в «лоб», то есть находить значения каждого члена и суммировать их, то при больших n потребуется выполнить большое число операций: умножений иn сложений. Кроме того, это может привести к потере точности за счет погрешности округлений.

Запишем многочлен в следующем виде:

.

Согласно этой формуле вычисление значения сводится к последовательному нахождению следующих величин:

;

;

;

…

;

.

Способ нахождения значения многочлена по вышеописанным формулам называется схемой Горнера. Для реализации этой схемы требуется n умножений и n сложений, то есть всего 2n арифметических действий. Схема Горнера является в общем случае самым оптимальным способом вычисления значения многочлена. Использование этой схемы не только экономит машинное время, но и повышает точность вычислений за счет уменьшения погрешности округления. Схема Горнера удобна также для реализации на ЭВМ благодаря цикличности вычислений и необходимости сохранять кроме коэффициентов многочлена и значения аргумента только одно значение промежуточной величины, а именно при текущем.

Интерполирование функции многочленом.

Теорема Вейерштрасса не дает способа построения аппроксимирующего многочлена, она устанавливает лишь принципиальную возможность этого построения. Для построения приближающих многочленов разработано много способов. Один из них – интерполирование, который заключается в следующем.

Пусть имеется таблица значений

x	x0	x1	x2	...	xn
y	y0	y1	y2	...	yn

Таблица 4.1.

некоторой функции , причем если, то. Задача состоит в том, чтобы найти такой многочлен степени не вышеn, который в заданных точках принимает те же значения, что и функция. Таким образом, близость интерполяционного многочлена для заданной функции состоит в том, что их значения совпадают на заданной системе точек (сетке).

Различают интерполяцию глобальную и локальную (или кусочную). Если один многочлен используется для интерполяции функциина всем рассматриваемом интервале изменения аргументаx, то говорят о глобальной интерполяции. В этом случае максимальная степень интерполяционного многочлена равна n, то есть на единицу меньше количества узлов интерполирования.

С геометрической точки зрения задача глобальной интерполяции заключается в построении такого многочлена степени не выше n, график которого проходит через данные точки , , ..., кривой.

Если интерполяционный многочлен строится отдельно для разных частей рассматриваемого интервала изменения x, то имеет место локальная интерполяция. Например, можно по трем лежащим рядом точкам построить кусочки парабол.

Теорема 4.2. Глобальный интерполяционный многочлен существует и единственен.

Доказательство.

Пусть – глобальная интерполяция функциипо системе узлов.

Учитывая, что (), можем записать

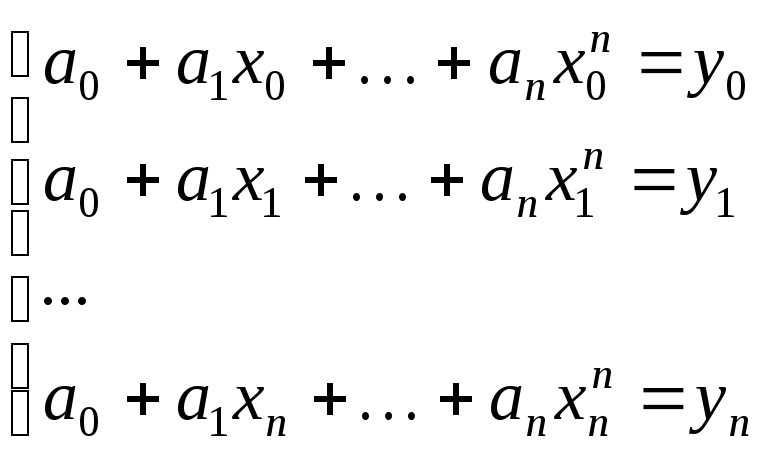. (4.1)

Это система для определения коэффициентов интерполяционного многочлена ,, …,. Как известно, многочлен однозначно задается системой своих коэффициентов.

Определитель системы (4.1) является определителем Вандермонда.

Этот определитель не равен 0, если среди чисел ,, …,нет равных. Так как при постановке задачи интерполирования мы потребовали, чтобы узлы были различны, то.

Тогда система (4.1) имеет единственное решение. Таким образом, для данной системы узлов существует единственный глобальный интерполяционный многочлен.

Из приведенных рассуждений следует способ построения интерполяционного многочлена: нужно составить и решить систему (4.1).

Пример.

x	0	1	2
y	0	1	4

, , ,.

Однако для практического применения этот способ является не удобным. Существуют способы, позволяющие построить интерполяционный многочлен более экономичными методами.