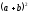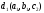Задание 4. Действия над векторами
Даны
длины двух векторов
и
известен угол между ними
.
Требуется найти:
1) длину соответствующего вектора в задачах: 1, 4, 7, 10, 13, 16, 19;
2) скалярное произведение в задачах: 2, 5, 8, 11, 14, 17, 20;
3) скалярный квадрат в задачах: 3, 6, 9, 12, 15, 18.
Таблица 3 – Данные задания 4 «Действия над векторами»
|
|
|
|
|
Найти |
|
|
|
|
|
Найти |
|
1 |
2 |
3 |
|
|
11 |
6 |
4 |
|
| |
|
2 |
4 |
2 |
|
|
12 |
5 |
2 |
|
| |
|
3 |
3 |
4 |
|
|
13 |
6 |
2 |
|
| |
|
4 |
2 |
4 |
|
|
14 |
3 |
6 |
|
| |
|
5 |
3 |
2 |
|
|
15 |
6 |
5 |
|
| |
|
6 |
2 |
5 |
|
|
16 |
1 |
6 |
|
| |
|
7 |
5 |
3 |
|
|
17 |
6 |
3 |
|
| |
|
8 |
4 |
3 |
|
|
18 |
2 |
6 |
|
| |
|
9 |
4 |
5 |
|
|
19 |
4 |
6 |
|
| |
|
10 |
5 |
4 |
|
|
20 |
5 |
1 |
|
|
Пример 4
Найти
длину вектора
,
если известно, что
Решение:
Задание 5. Координаты вектора в новом базисе
Показать, что система векторов
,
,
образует базис, разложить вектор
по этому базису. Решить систему уравнений,
используя формулы Крамера. Координаты
векторов даны в таблице 6.
Таблица 6 – Данные задания 5 «Координаты вектора в новом базисе»
|
№ |
|
|
|
|
|
1 |
(3,1,4) |
(-1,-3,1) |
(-2,1,-5) |
(3,-1,4) |
|
2 |
(5,3,3) |
(3,-2,2) |
(2,4,1) |
(9,-5,6) |
|
3 |
(1,3,2) |
(1,5,2) |
(-2,-1,3) |
(-1,0,5) |
|
4 |
(2,3,3) |
(4,1,-4) |
(1,2,5) |
(3,1,5) |
|
5 |
(4,2,1) |
(-1,-2,1) |
(2,1,2) |
(9,3,5) |
|
6 |
(1,3,4) |
(-3,1,1) |
(1,-2,-1) |
(-2,-1,3) |
|
7 |
(3,1,1) |
(1,2,4) |
(-2,-1,-5) |
(5,3,1) |
|
8 |
(1,2,2) |
(3,5,-1) |
(-2,2,3) |
(-1,3,-2) |
|
9 |
(2,4,1) |
(-1,-2,-3) |
(-1,-3,3) |
(-1,-3,-2) |
|
10 |
(2,3,4) |
(2,-2,3) |
(-1,2,1) |
(-3,1,2) |
|
11 |
(2,2,1) |
(-3,4,-2) |
(2,-5,-3) |
(3,-4,-7) |
|
12 |
(3,2,1) |
(2,1,-4) |
(5,3,3) |
(6,3,0) |
|
13 |
(2,3,1) |
(-1,2,-3) |
(-1,2,-5) |
(3,1,2) |
|
14 |
(1,5,2) |
(2,3,3) |
(4,-4,1) |
(3,5,1) |
|
15 |
(4,1,2) |
(2,2,1) |
(-1,1,-2) |
(-1,3,1) |
|
16 |
(3,1,1) |
(-1,4,3) |
(-1,-1,-2) |
(2,3,-1) |
|
17 |
(1,4,2) |
(-2,-5,-1) |
(3,1,1) |
(0,-5,1) |
|
18 |
(3,1,5) |
(-1,-3,2) |
(1,-2,2) |
(-2,1,3) |
|
19 |
(1,2,3) |
(-2,-4,-1) |
(1,3,-3) |
(1,4,1) |
|
20 |
(2,2,3) |
(2,3,4) |
(-3,2,1) |
(-6,5,3) |
Пример 5
Показать, что
система векторов
,
,
образует базис, найти разложение
в этом базисе.
Решение: Покажем,
что векторы
,
,
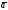образуют базис. Найдём определитель,
составленный из координат этих векторов.
Т.к. определитель не равен нулю, следовательно, векторы линейно независимы и образуют базис.
Разложим вектор
по векторам данного базиса:
,
здесь
,
,
−
искомые координаты вектора
в
базисе
,
,
.В координатной
форме это уравнение
(1,
1, 2)+
(5,
3, -1) +
(2,
3, 1) = (5, 2, 2) принимает вид:
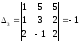
Решим
приведённую систему по формулам Крамера
;
для этого вычислим дополнительные
определители
полученные из основного определителя
Δ заменой
–го
столбца столбцом свободных членов:
;
.
Таким
образом, находим коэффициенты разложения
вектора
:
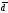Задание 6. Решение задач линейного программирования симплексным методом
Затраты
трёх видов сырья А, В, С на производство
единицы каждого из трёх типов продукции
заданы векторами –
,
,
.
Запасы каждого вида сырья заданы
вектором
,
прибыль от реализации единицы продукции
каждого типа − вектором
.
Определить оптимальный план выпуска
продукции, при котором прибыль от
реализации выпущенной продукции будет
максимальной. Составить математическую
модель задачи, решить задачу
симплексным методом. Составить
двойственную задачу к данной и найти
её решение.
Таблица 7 – Данные задания 6 «Симплексный метод решения задач»
|
№ |
|
|
|
|
|
|
1 |
(3, 2, 4) |
(5, 4, 3) |
(6, 2, 2) |
(270, 90, 190) |
(2, 1,1) |
|
2 |
(3, 2, 4) |
(1, 2, 3) |
(5, 4, 1) |
(230, 210, 130) |
(1, 2, 3) |
|
3 |
(3, 2, 4) |
(4, 7, 6) |
(2, 1, 1) |
(230, 270, 190) |
(1, 1, 2) |
|
4 |
(7, 1, 3) |
(1, 2, 1) |
(3, 1, 6) |
(200, 90, 150) |
(3, 1, 2) |
|
5 |
(4, 5, 3) |
(4, 7, 6) |
(2, 1, 1) |
(230, 270, 190) |
(2, 1, 3) |
|
6 |
(2, 5, 4) |
(3, 2, 7) |
(6, 1, 2) |
(190, 140, 100) |
(2, 1, 3) |
|
7 |
(2, 6, 1) |
(8, 4, 3) |
(1, 5, 4) |
(325, 325, 215) |
(1, 3, 2) |
|
8 |
(5, 3, 1) |
(3, 5, 4) |
(2, 1, 3) |
(270, 240, 145) |
(3, 1, 2) |
|
9 |
(4, 1, 3) |
(1, 3, 3) |
(2, 4, 5) |
(200, 120, 260) |
(1, 2, 3) |
|
10 |
(6, 1, 2) |
(9, 1, 1) |
(3, 2, 4) |
(480, 90, 140) |
(2, 5, 4) |
|
11 |
(2, 2, 4) |
(1, 1, 5) |
(3, 5, 1) |
(150, 190, 230) |
(2, 3, 4) |
|
12 |
(4, 2, 5) |
(2, 6, 1) |
(5, 1, 2) |
(200, 150, 160) |
(2, 3, 1) |
|
13 |
(3, 2, 1) |
(5, 3, 4) |
(4, 4, 5) |
(160, 120, 180) |
(2, 1, 3) |
|
14 |
(2, 3, 5) |
(4, 1, 3) |
(3, 8, 1) |
(100, 150, 130) |
(1, 2, 1) |
|
15 |
(3, 7, 2) |
(5, 1, 2) |
(1, 1, 6) |
(125, 165, 150) |
(3, 2, 1) |
|
16 |
(9, 3, 1) |
(4, 3, 5) |
(1, 4, 1) |
(290, 175, 155) |
(1, 2, 1) |
|
17 |
(2, 6, 4) |
(4, 2, 1) |
(1, 3, 5) |
(130, 200, 150) |
(2, 1, 1) |
|
18 |
(1, 4, 2) |
(1, 5, 3) |
(7, 1, 6) |
(175, 170, 210) |
(1, 2, 1) |
|
19 |
(2, 3, 2) |
(2, 3, 4) |
(7, 4, 1) |
(150, 160, 280) |
(1, 1, 2) |
|
20 |
(3, 1, 2) |
(1, 2, 4) |
(5, 3, 1) |
(170, 115, 105) |
(2, 2, 3) |
Пример 6. Составим математическую модель.
Пусть предприятие выпустит x1 единиц продукции I, х2 единиц продукции II, х3 единиц продукции III.
Расход
сырья А на все виды продукции –
.
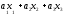По условию задачи расход сырья А не
должен превышать запаса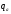
,
т.е.
≤
Аналогично составляем ограничения
расхода сырья В и С. Получим систему
неравенств:
Прибыль от реализации выпущенной продукции будет равна
.
Запишем модель задачи:
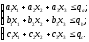(12)
.
(13)
(13) называют целевой функцией.
Пусть
(7,2,5),
d2(0,3,1),
d3(5,2,1),
Q(220,140,100),
Р(2,1,1)
(14)
.
(15)
Введем балансовые
переменные
,
,
в каждое неравенство для приведения
модели к каноническому виду
(16)
,
(j=1,2,…6)
.
(17)