
- •Введение
- •Раздел 1. Элементы аналитической геометрии
- •Раздел 2. Элементы линейной алгебры
- •Раздел 3. Элементы векторной алгебры
- •Раздел 4. Элементы линейного программирования
- •Список рекомендуемой основной и дополнительной литературы
- •Контрольные задания, правила выполнения и оформления контрольных работ
- •Задание 2. Линии второго порядка
- •Задание 4. Действия над векторами
- •Алгоритм симплексного метода
Задание 2. Линии второго порядка
Уравнение кривой привести к каноническому виду и построить линию.
Таблица 3 – Данные задания 2 «Линии второго порядка»
|
Задача № |
|
Уравнения кривых |
|
Задача № |
|
Уравнения кривых |
|
1 |
а |
|
11 |
а |
| |
|
б |
б | |||||
|
2 |
а |
|
12 |
а |
| |
|
б |
б | |||||
|
3 |
а |
|
13 |
а |
| |
|
б |
б | |||||
|
4 |
а |
|
14 |
а |
| |
|
б |
б | |||||
|
5 |
а |
|
15 |
а |
| |
|
б |
б | |||||
|
6 |
а |
|
16 |
а |
| |
|
б |
б | |||||
|
7 |
а |
|
17 |
а |
| |
|
б |
б | |||||
|
8 |
а |
|
18 |
а |
| |
|
б |
б | |||||
|
9 |
а |
|
19 |
а |
| |
|
б |
б | |||||
|
10 |
а |
|
20 |
а |
| |
|
б |
|
б |
Пример 2. Уравнение кривой привести к каноническому виду и построить линию.
х2 + 4у2 - 4х + 16у - 16 = 0;
9x2-4y2-54x-8y+41 = 0.
Решение:
х2 + 4у2 - 4х + 16у - 16 = 0. Приведём данную кривую к каноническому виду и построим.
Выделим полные квадраты при х и у:
(х2-4х+4)-4+4(у2+4у+4)-16-16=0
, (х-2)2+4(у+2)2-36=0,
(х-2)2+4(у+2)2=36,
 .
.
Получили каноническое уравнение эллипса вида
 .
(7)
.
(7)
Центр
эллипса лежит в точке O/(α,β),
оси параллельны осям координат ОХ и OY.
Точка O/(2,-2)
– центр данного эллипса. Отложим от
точки O/
отрезки
 в направлениях, параллельных ОХ иOY,
CС/=2
в направлениях, параллельных ОХ иOY,
CС/=2 =12
ВВ/=2
=12
ВВ/=2 =6
(рисунок 2).
=6
(рисунок 2).

Рисунок 2 ─ Эллипс
2) 9x2-4y2-54x-8y+41 = 0. Приведём данную кривую к каноническому виду и построим.
Выделим полные квадраты при х и у:
9(х2-6х+9)-81-4(у2+2у+1)+4+41 = 0 , 9(х-3)2-4(у+1)2-36 = 0,
9(х-3)2─
4(у+1)2
= 36 ,

Получили каноническое уравнение гиперболы вида
 .
(8)
.
(8)
Центр
гиперболы лежит в точке А(α,β), оси
параллельны осям координат. Центр данной
гиперболы лежит в точке А(3,-1),
 =2,
=2, =3.
Построим основной прямоугольник
гиперболы, откладывая от точки А отрезки
=3.
Построим основной прямоугольник
гиперболы, откладывая от точки А отрезки =2,
=2,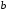 =3
в направлениях, параллельных основным
осям координат.BB/=2∙
=3
в направлениях, параллельных основным
осям координат.BB/=2∙ =4,
СС/=2∙
=4,
СС/=2∙ =6.
Диагонали прямоугольника будут являться
асимптотами. Вершиныгиперболы
– точки B
и B/
(рисунок
3).
=6.
Диагонали прямоугольника будут являться
асимптотами. Вершиныгиперболы
– точки B
и B/
(рисунок
3).

Рисунок 3 ─ Гипербола
Задание 3. Системы линейных уравнений
1) Решить систему линейных уравнений матричным способом.
2) Найти базисное решение системы уравнений методом Жордана – Гаусса.
Таблица 4 – Данные задания 3 « Системы линейных уравнений»
|
№ |
Системы уравнений |
|
1 |
1)
|
|
2 |
1)
|
|
3 |
1)
|
|
4 |
1)
|
|
5 |
1)
|
|
6
|
1)
|
|
7 |
1)
|
|
8 |
1) |
|
9 |
1)
|
|
10 |
1)
|
|
11 |
1)
|
|
12 |
1)
|
|
13 |
1)
|
|
14 |
1)
|
|
15 |
1)
|
|
16 |
1)
|
|
17 |
1)
|
|
18 |
1)
|
|
19 |
1)
|
|
20 |
1)
|
Пример 3
1) Решить систему уравнений матричным способом.

Решение. Обозначим
X
= −
матрица-столбец неизвестных переменных;
−
матрица-столбец неизвестных переменных;
 −матрица
коэффициентов при неизвестных или
основная матрица;
−матрица
коэффициентов при неизвестных или
основная матрица;
 − матрица
свободных членов системы уравнений.
− матрица
свободных членов системы уравнений.
Систему уравнений можно представить в матричном виде А ∙ X = А0.
Тогда решение системы имеет вид:
Х = А-1 ∙ А0, (9)
где
А-1
–
обратная матрица к квадратной матрице
А = .
.
Формула для вычисления обратной матрицы
А--1=

 .
(10)
.
(10)
 –
определитель
матрицы А, который вычисляется по формуле
–
определитель
матрицы А, который вычисляется по формуле

Вычислим определитель матрицы системы:

Т.к. определитель матрицы А не равен 0, то матрица А невырожденная , для неё существует обратная матрица A-1.
Вычислим
алгебраические дополнения
 для каждого элемента
для каждого элемента основной матрицы по формуле
основной матрицы по формуле ,
где
,
где – минор того же элемента
– минор того же элемента .
.
Минор
 элемента
элемента – это определитель, полученный из
данного определителя вычеркиваниемi-й
строки и j-гo
столбца.
– это определитель, полученный из
данного определителя вычеркиваниемi-й
строки и j-гo
столбца.









Таким образом, по формуле (10) имеем следующую обратную матрицу:

Согласно формуле (9), получаем:

Проверка:
Подставим
найденные числа вместо переменных
 в исходную систему уравнений:
в исходную систему уравнений:

Получили верные числовые равенства, следовательно, решение найдено верно.
Ответ:
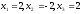 .
.
Приведение системы линейных уравнений к системе с базисом методом Жордана – Гаусса
Система уравнений называется системой с базисом, если каждое уравнение системы содержит переменную с коэффициентом 1, отсутствующую в других уравнениях.
Например, рассмотрим систему уравнений с базизом:

Переменные
 – базисные,
– базисные, – свободные. Базисное решение
– свободные. Базисное решение .
.
Алгоритм метода Жордана – Гаусса
Составляем таблицу Жордана – Гаусса.
Выбираем разрешающий элемент из коэффициентов
 при неизвестных,i-я
строка и j-й
столбец будут называться разрешающими.
при неизвестных,i-я
строка и j-й
столбец будут называться разрешающими.Элементы i-й разрешающей строки делят на разрешающий элемент и полученные частные записывают в i-ю строку следующей таблицы.
Все элементы j-го столбца следующей таблицы обращаются в 0, кроме элемента, стоящего на месте разрешающего, он равен 1.
Все остальные элементы следующей таблицы вычисляются по “правилу прямоугольников”:

 .
(11)
.
(11)
2) Найти базисное решение системы уравнений:

Составим таблицу Жордана – Гаусса.
Столбец
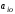 содержит свободные члены соответствующих
уравнений, столбцы
содержит свободные члены соответствующих
уравнений, столбцы содержат коэффициенты при соответствующих
переменных в уравнениях. В столбец “Б”
будем записывать базисные переменные
соответствующих уравнений.
содержат коэффициенты при соответствующих
переменных в уравнениях. В столбец “Б”
будем записывать базисные переменные
соответствующих уравнений.
|
Б |
|
|
|
|
|
|
|
|
|
1 2 0 |
2 -1 3 |
-1 0 -2 |
-1
1 -1 |
-2 2 -2 |
2 -1 -1 |
таблица 1 |
|
|
3 2 2 |
1 -1 2 |
-1 0 -2 |
0 1 0 |
0 2 0 |
1 -1 -2 |
таблица 2 |
|
|
3 5 8 |
1 0 4 |
-1 -1 0 |
0 1 0 |
0 2 0 |
1 0 0 |
таблица 3 |
|
|
1 5 2 |
0 0 1 |
-1 -1 0 |
0 1 0 |
0 2 0 |
1 0 0 |
таблица 4 |
1. Выбираем в
таблице 1 разрешающий элемент, любой
из коэффициентов, не равный нулю,
например
 .
.
2. Элементы разрешающей строки делим на 1 и записываем полученные значения во второй строке таблицы 2.
3. В
разрешающем столбце таблицы 2 остальные
элементы обращаются в ноль. Во
втором уравнении неизвестная
 становится базисной.
становится базисной.
4. Оставшиеся элементы таблицы 2 находим по правилу прямоугольника.
Приведем расчёты некоторых из них:
 ,
,
 ,
, ,
,
 ,
,
 ,
,
 .
.
5. Повторяя алгоритм
метода Жордана – Гаусса, перейдем к
таблице 4. Полученная система уравнений
является системой с базисом. Базисные
переменные –
 ,
, ,
, ,
свободные ─
,
свободные ─ ,
, .
.

Чтобы записать
базисное решение, базисные переменные
приравниваем к соответствующим свободным
членам, свободные переменные ─ к нулю.
Полученное базисное решение имеет
вид .
.





















 2)
2)

 2)
2)

 2)
2)

 2)
2)

 2)
2)

 2)
2)

 2)
2)

 2)
2)
 2)
2)

 2)
2)
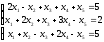
 2)
2)

 2)
2)

 2)
2)

 2)
2)
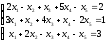
 2)
2)

 2)
2)

 2)
2)

 2)
2)

 2)
2)

 2)
2)














