
- •II. Пределы и непрерывность
- •§ 4. Пределы функций
- •Предел дробно-рациональной функции в точке
- •Пределы дробно-рациональных функций с квадратичными выражениями
- •Предел дробно-рациональной функции в бесконечности
- •Пределы иррациональных функций
- •Примеры сопряжённых выражений
- •Тригонометрические пределы. Первый замечательный предел
- •Второй замечательный предел
- •§ 5. Непрерывность функций
- •Исследование кусочно-заданных функций на непрерывность
- •Непрерывность дробно-рациональных функций
- •Непрерывность некоторых сложных функций
II. Пределы и непрерывность
§ 4. Пределы функций
«Предел функции» – более общее понятие, чем «значение функции в точке».
Не всегда аргумент
можно подставить в формулу функции.
Так, функция
![]() не имеет смысла в точке
не имеет смысла в точке![]() ,
но при
,
но при![]() получается
получается![]() .
.
Функция
![]() не вычисляется в точке
не вычисляется в точке![]() ,
но при
,
но при![]() оказывается, что
оказывается, что![]() .
.
В 1-м случае говорят,
что предел в точке 0 равен 2:
![]() .
Во 2-м случае предел в точке
.
Во 2-м случае предел в точке![]() равен –3:
равен –3: .
.
Кроме того, функции не определяются в бесконечности, поскольку такое понятие не выражается числом. Между тем предел в бесконечности находится по стандартным правилам и нередко достаточно просто.
Например, функция
![]() при
при![]() вначале быстро возрастает, однако при
бесконечно большом аргументе стремится
к 0:
вначале быстро возрастает, однако при
бесконечно большом аргументе стремится
к 0:![]() .
.
Также хорошо
известно, что функция
![]() при
при![]() .
.
Для работы необходимо вспомнить, что
а) функции
![]() ,
где
,
где![]() ,
называютосновными
элементарными;
,
называютосновными
элементарными;
б) функции, составленные из основных элементарных при помощи конечного числа арифметических операций и суперпозиций (взятия функции от функции), называют элементарными.
Если функция
![]() элементарна, то при вычислении
элементарна, то при вычислении![]() ,
когда
,
когда![]() – число, вначале пробуют подставить
– число, вначале пробуют подставить![]() в функцию
в функцию![]() – найти
– найти![]() .
.
Если результат
получается, как обычное значение функции
– это и есть ответ. Если функция
неэлементарна или при подстановке
возникает неопределённость
![]()
![]() ,
,![]() ,
применяют разные правила и схемы
вычисления пределов.
,
применяют разные правила и схемы
вычисления пределов.
Предел дробно-рациональной функции в точке
Пусть даны точка
![]() и функция
и функция![]() ,
где
,
где![]() и
и![]() – некоторые многочлены. Надо найти
– некоторые многочлены. Надо найти![]() .
.
Найдём
![]() и
и![]() .
Полученные числа обозначим соответственноP
и Q.
Возможны 4 случая:
.
Полученные числа обозначим соответственноP
и Q.
Возможны 4 случая:
1)
![]() ,
тогда
,
тогда![]() – это обычное число (не обязательно
целое);
– это обычное число (не обязательно
целое);
2)
![]() ,
тогда
,
тогда![]() ;
;
3)
![]() ,
тогда
,
тогда![]() ;
;
4)
![]() ,
тогда
,
тогда![]() и
и![]() раскладываются на скобки так, что
раскладываются на скобки так, что
 для всех
для всех
![]() ,
,
где
![]() – какие-то многочлены (полиномы).
Находим
– какие-то многочлены (полиномы).
Находим
![]() и
и![]() и приходим к одному из случаев 1, 2 или
3.
и приходим к одному из случаев 1, 2 или
3.
Проще говоря,
– в 1-м и 2-м случаях предел равен значению функции в точке;
– в 3-м не равен конкретному числу и обозначается символом бесконечности;
– в 4-м случае надо
разложить числитель и знаменатель на
скобки, сократить одинаковые и подставить
число
![]() заново.
заново.
ПР1. Найдите пределы простой подстановкой:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
д)
;
д)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() .
.
Пример 1. Подстановкой можно найти, что
а)
![]() ;
;
б)
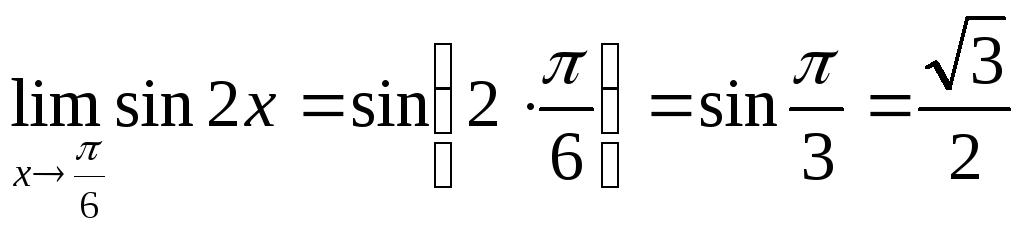 ;
;
в)
![]() .
.
ПР2.
Найдите пределы, подставив точку
![]() в функцию
в функцию![]() :
:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
д)
;
д)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() ;
;
3) а)
![]() ; б)
; б)![]() ;
в)
;
в)![]() ; г)
; г)![]() ; д)
; д)![]() ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
г)
;
г)![]() ;
;
5) а)
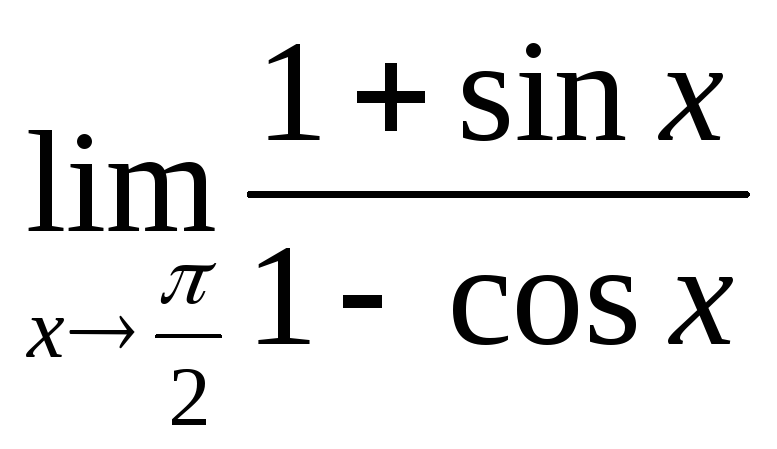 ;
б)
;
б)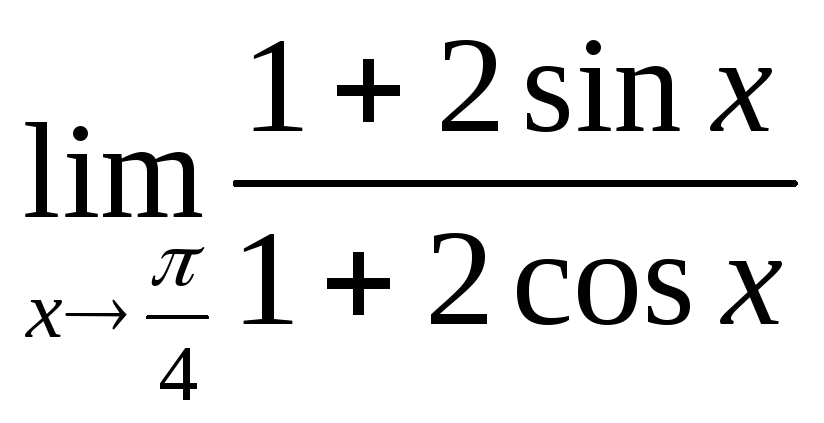 ;
в)
;
в)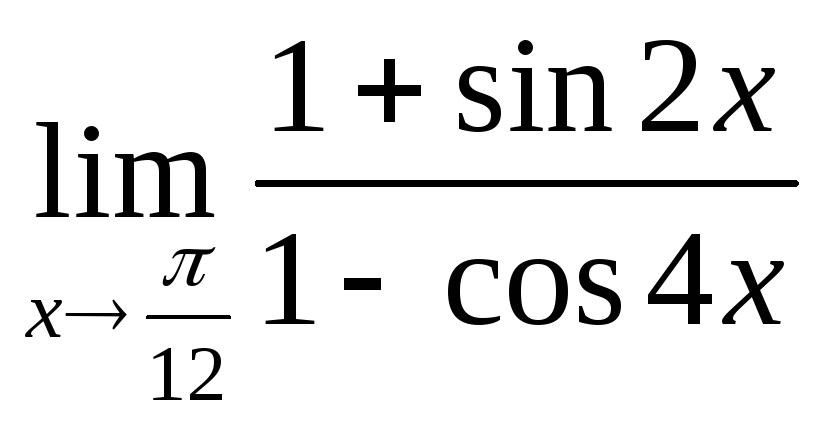 ;
г)
;
г)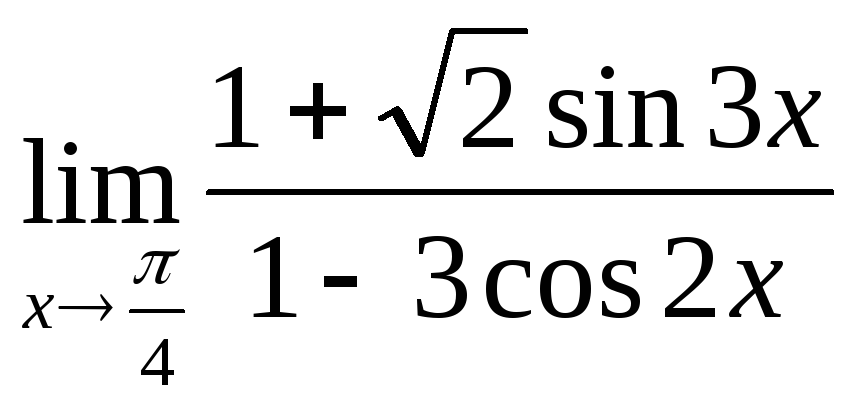 .
.
Пример 2. Так же, как в примере 1,
а)
![]() ;
;
б)
![]() ;
;
в)
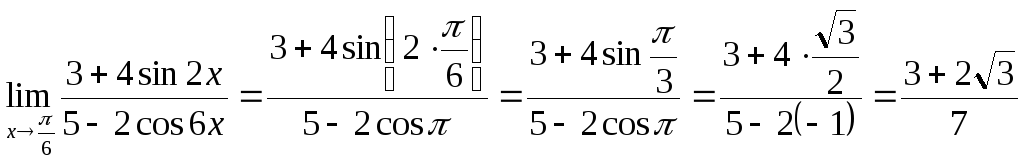 (не
(не![]() !)
!)
ПР3. Подставив
точку
![]() в функцию
в функцию![]() ,
проверьте, что пределы равны 0:
,
проверьте, что пределы равны 0:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)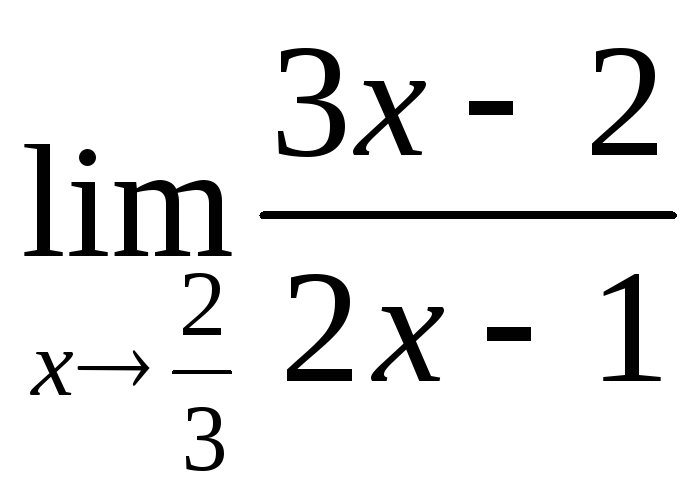 ;
д)
;
д)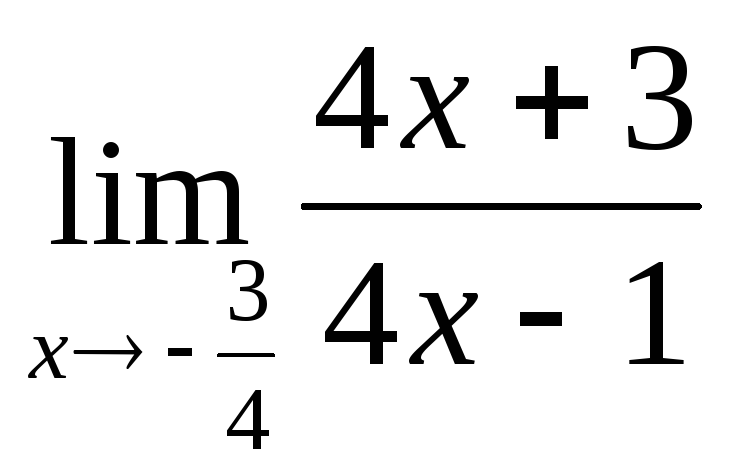 ;
;
2) а)
![]() ;
б)
;
б)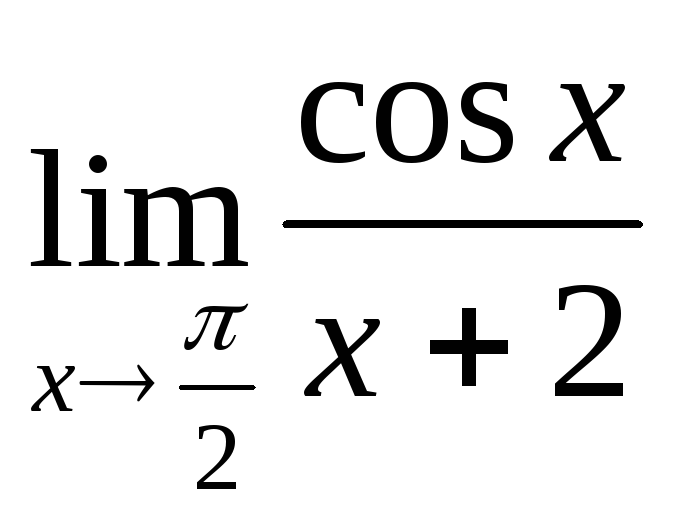 ; в)
; в)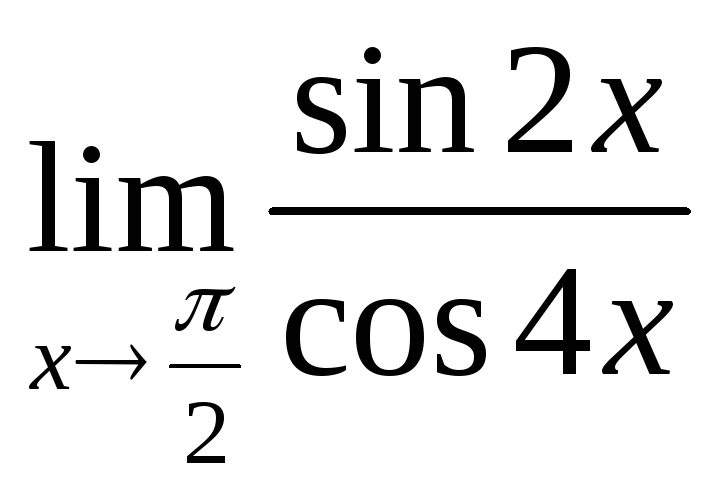 ; г)
; г)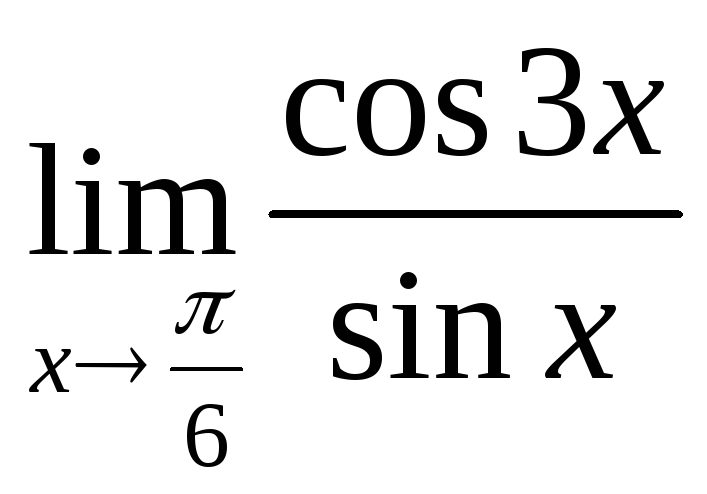 ;
д)
;
д)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
г)
;
г)![]() ;
д)
;
д)![]() ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
5) а)
![]() ; б)
; б)![]() ;
в)
;
в)![]() ; г)
; г)![]() .
.
Пример 3. Простая подстановка показывает, что
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
ПР4. Проверьте, что указанные пределы равны бесконечности:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)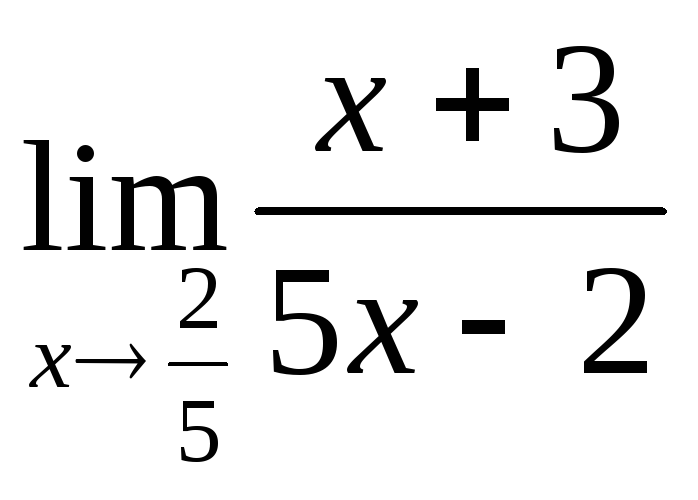 ; д)
; д)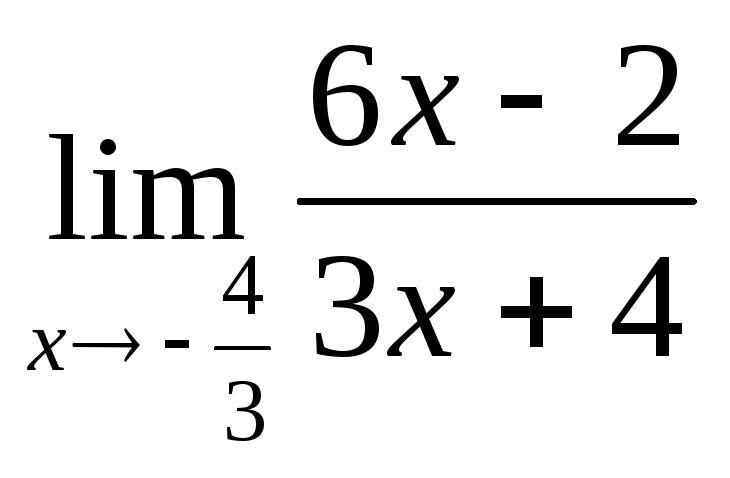 ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)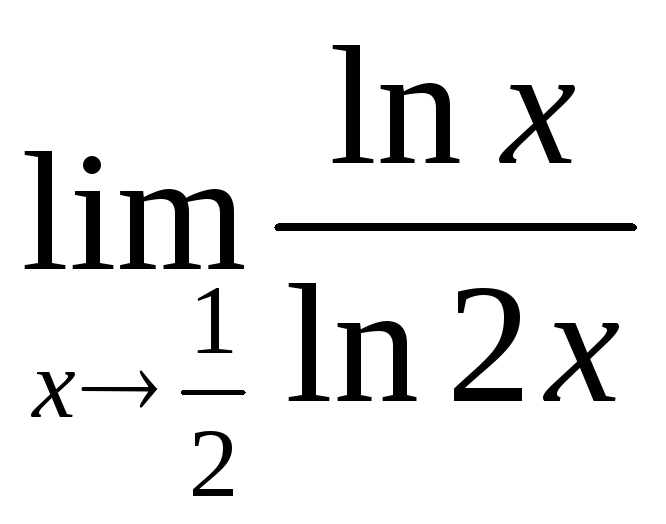 ; г)
; г)![]() ; д)
; д)![]() ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)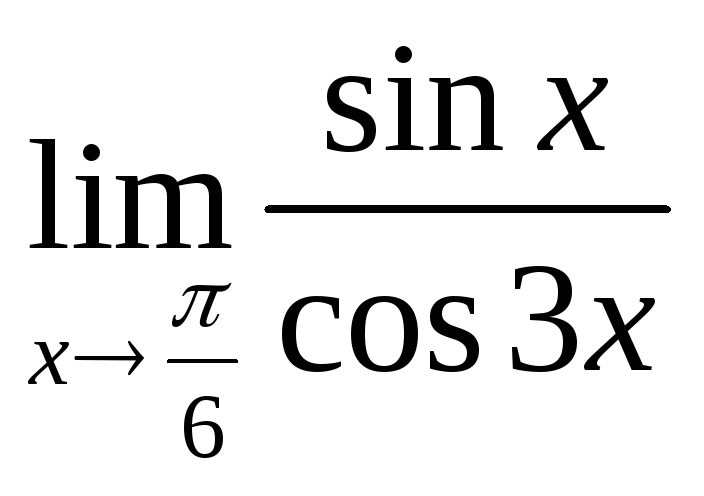 ; г)
; г)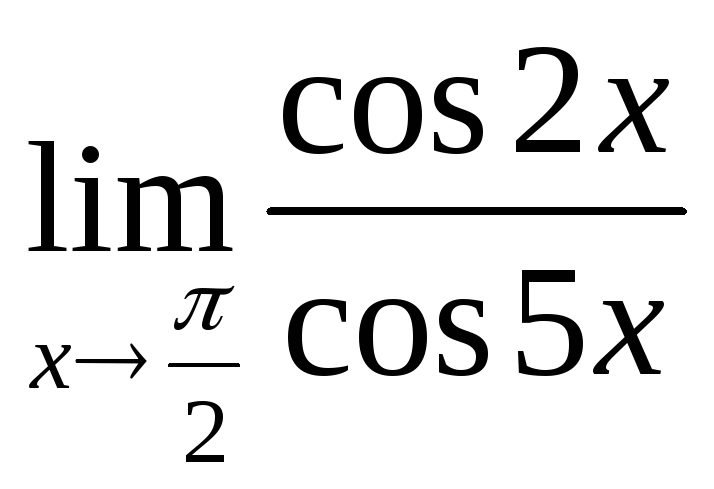 ; д)
; д)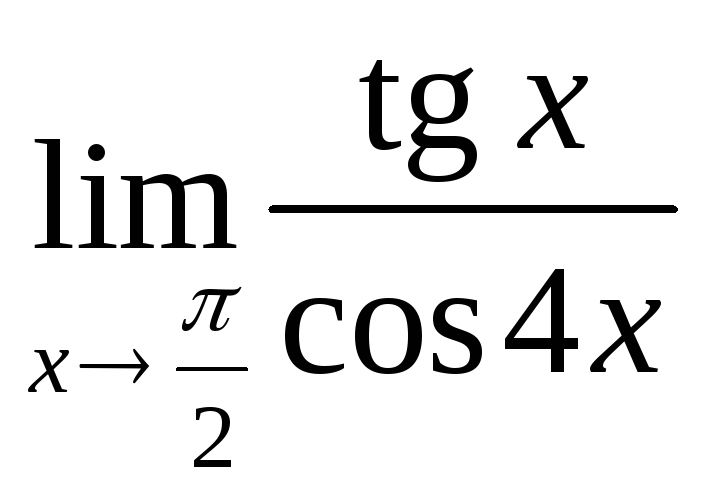 .
.
Пример 4. Поскольку знаменатель равен 0, то
а)
![]() ;
;
б)
![]() ;
;
в)
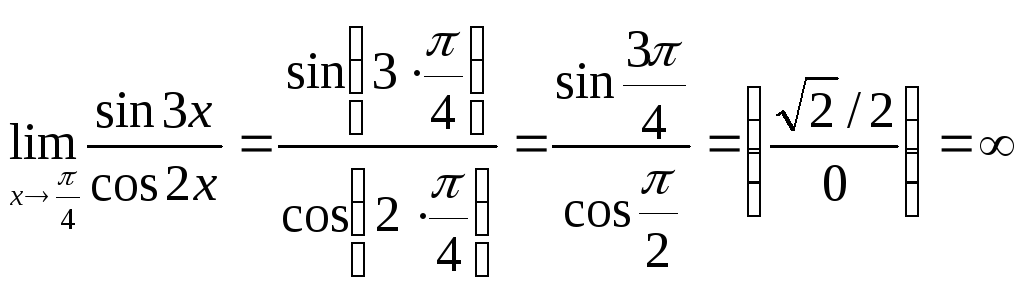 .
.
ПР5. Раскройте
неопределённость
![]() ,
разложив дробь на множители-скобки и
сократив одинаковые скобки в числителе
и в знаменателе:
,
разложив дробь на множители-скобки и
сократив одинаковые скобки в числителе
и в знаменателе:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)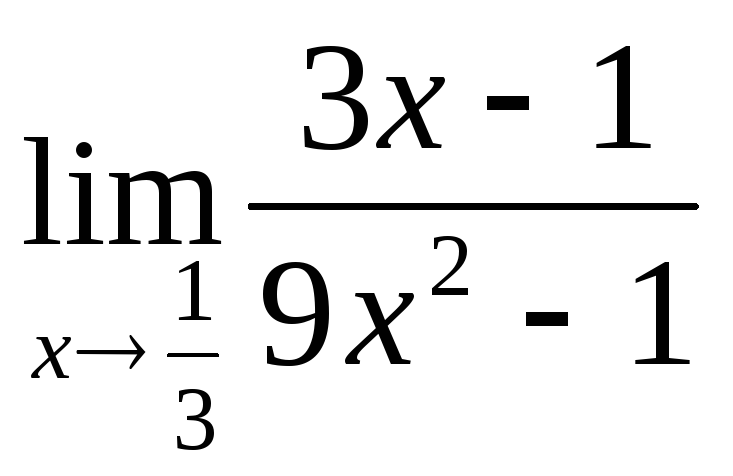 ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)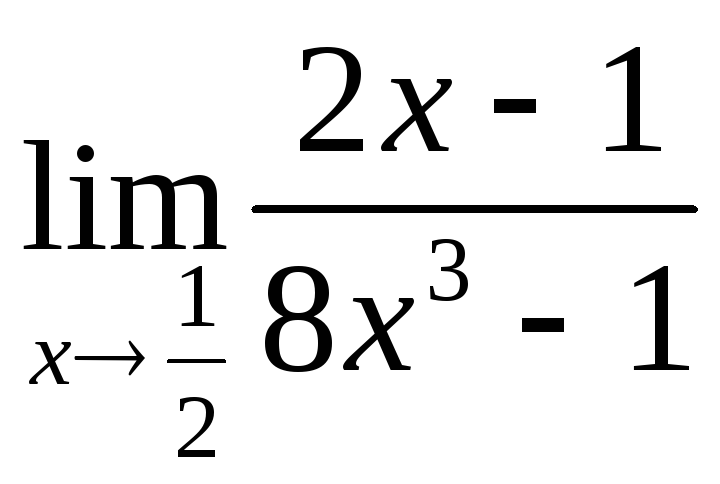 ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)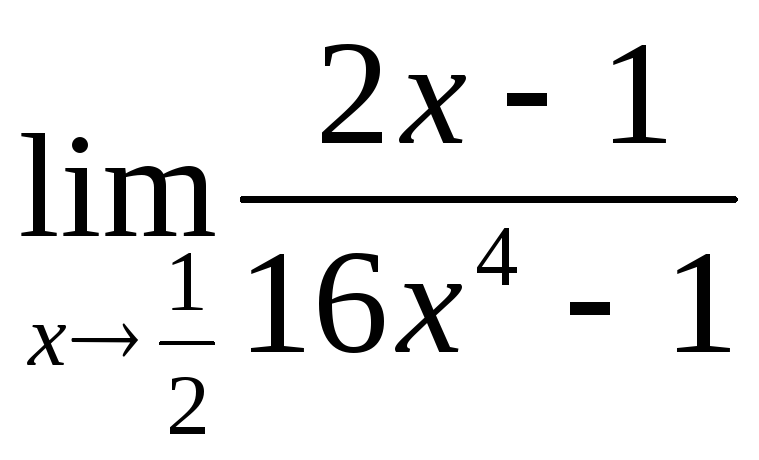 ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() .
.
Замечание 1. Вам понадобятся формулы
![]() ;
;
![]() ;
;
![]() .
.
Сумма квадратов
![]() на действительные множителине
раскладывается.
на действительные множителине
раскладывается.
Пример 5.

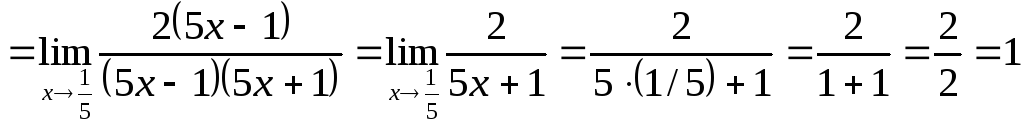 .
.
Также можно было
вынести за скобки числа 10 и 25 и сократить
на
![]() .
.
Замечание 2. Обратите внимание, что попытка подставить число в первоначальную дробь берётся в скобки как приводящая к неопределённости (также заключаемой в скобки). Этим подчёркивается, что арифметическое выражение, взятое в скобки, не имеет смысла и потому не равно самому пределу. В то время как предел равен конкретному числу, что и выясняется при решении.
Замечание 3. Скобки при появлении необычных ситуаций ставят, чтобы отличать последние от бессмысленных выражений. Например,
![]() – деление одной бесконечно малой
величины на другую;
– деление одной бесконечно малой
величины на другую;
![]() – деление числа 1 на бесконечно малую
величину;
– деление числа 1 на бесконечно малую
величину;
![]() и
и![]() – действия или величины, противоречащие
основам математики.
– действия или величины, противоречащие
основам математики.
Пример 6.
![]()
![]() .
.
