
Глава III
ОД11 (Правильные ответы)
|
№ |
|
№ |
|
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
|
31 |
|
32 |
|
|
33 |
|
34 |
|
|
35 |
|
36 |
|
|
37 |
|
38 |
|
|
39 |
|
40 |
|
|
41 |
|
42 |
|
|
43 |
|
44 |
|
|
45 |
|
46 |
|
|
47 |
|
48 |
|
|
49 |
|
50 |
|
ОД13.
|
1)
|
2)
| ||
|
3)
|
4)
| ||
|
5)
|
6)
| ||
|
7)
|
8)
| ||
|
9)
|
10)
| ||
|
11)
|
12)
| ||
|
13)
|
14)
| ||
|
15)
| |||
|
16)
|
17) | ||
|
18)
|
19)
| ||
|
20)
|
21)
| ||
|
22)
|
23) | ||
|
24)
|
25)
| ||
|
26)
|
27)
| ||
|
28)
|
29) |
30)
| |
Глава IV
ЧП4.(во всех примерах![]() ,
,
указаны соответственно
![]() ).
).
а) 1/16; 1/36; 5/24; б) 1/36; 1/16; 5/24; в) 1/16; 1/100; 7/40;
г) 1/100; 1/64; 9/80; д) 1/144; 1/4; 7/24; е) 1/4; 1/16; 3/8;
ж) при
![]() будет
будет![]() ;
;
при
![]() функция неограниченно растёт;
функция неограниченно растёт;
з) при
![]() будет
будет![]() ;
;
при
![]() функция неограниченно растёт;
функция неограниченно растёт;
ЧП5.(во всех примерах![]() ,
,
указаны соответственно
![]() ).
).
а) 1; 9/4; 13/4; б) 9/4; 1; 13/4; в) 1; 25/4; 29/4; г) 25/4; 4; 41/4;
д) 9; 1/4; 37/4; е) 1/4; 1; 5/4; ж) 0; 4; 4; з) 9/4; 0; 9/4.
ЧП6
1) а–б)
![]() ; в–г)
нет экстремума в
; в–г)
нет экстремума в![]() ;
;
д)
![]() при любомc; е)
при любомc; е)![]() при любомc;
при любомc;
2) а)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
б)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
в)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
г)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
д) нет экстремума в
![]() и
и![]() ;
;
е) нет стационарных точек, возрастает
от
![]() до
до![]() по каждой переменной;
по каждой переменной;
3) а)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
б)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
в)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
г) нет стационарных точек, убывает по yпри любом фиксированномx;
д)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
е)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
4) а)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
б)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
в)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
г) необходимо дополнительное исследование
в точках
![]() и
и![]() ;
;
5) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
также во всех примерах а–г) нет экстремума
в
![]() ;
;
6) а)
![]() ; б)
нет экстремума в
; б)
нет экстремума в![]() ; в)
; в)
![]() ;
;
г)
![]() ,
нет экстремума в
,
нет экстремума в![]() ; д)
; д)
![]() ;
;
е)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
ж)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
з)
![]() ,
нет экстремума в
,
нет экстремума в![]() и
и![]() ;
;
7) а)
![]() ,
в
,
в![]() – дополнительное исследование (нет
экстремума);
– дополнительное исследование (нет
экстремума);
б)
![]() ,
в
,
в![]() нет экстремума, в
нет экстремума, в![]() – дополнительное исследование (нет
экстремума);
– дополнительное исследование (нет
экстремума);
в)
![]() ,
в
,
в![]() ,
,![]() и
и![]() нет экстремума;
нет экстремума;
г)
![]() ,
в
,
в![]() ,
,![]() и
и![]() нет экстремума.
нет экстремума.
Содержание
Предисловие …..………………………………………………….………….…….... 3
I. ЗАДАЧИ ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ………………………………… 5
§1. Линейная функция. Уравнение прямой. Парабола ………………………….... 5
§2. Элементарные преобразования графиков …….………………………….……. 9
§3. Аналитическое задание функций …………………………………………….. 13
II. ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ …………………………………………….. 16
§4. Пределы функций ……………………………………………………………… 16
§5. Непрерывность функций ……………………………………………………… 33
III. ПРОИЗВОДНАЯ И ИССЛЕДОВАНИЕ ФУНКЦИЙ …………………………53
§6. Основы дифференцирования функций ……………….……………………… 53
§7. Логарифмическое дифференцирование ……………………………………… 69
§8. Правило Лопиталя – Бернулли ……………………………………………….. 72
§9. Исследование функций и построение графиков …………………………….. 75
IV. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ …………………………….…….…….. 82
§10. Основы дифференцирования функции двух переменных ………………… 82
Несколько замечаний о литературе ……………………………………………… 91
Библиографический список ……………………………………….……………… 92
ОТВЕТЫ И УКАЗАНИЯ ………………………………………….……………… 93
Глава I ………………………………………….…………………………… 93
Глава II ………………………………………….……………………………94
Глава III ………………………………………….………………………….. 95
Глава IV ………………………………………….………………………….. 97
Учебное издание
Евгений Анатольевич Мясников
ПРАКТИКУМ
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ.
Часть 1
Учебное пособие
Редактор Г.С. Одинцова
Подписано к печати 2012 г. Формат 60х84/16. Бумага писчая.
Печать цифровая. Усл.печ.л. 5,8. Уч.-изд. л. 4,2. Тираж 100 экз.
Заказ №_______________________________________________________
680042, г. Хабаровск, ул. Тихоокеанская, 134, РИЦ ХГАЭП

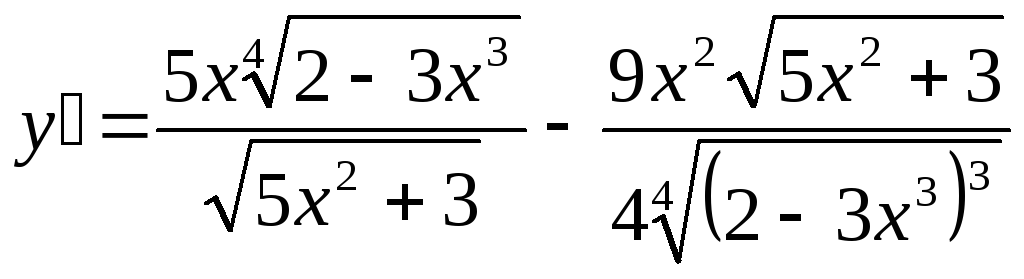 ;
;