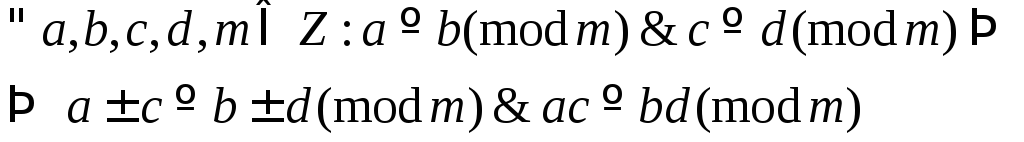- •Оглавление
- •Раздел 1. Математические основы криптографии
- •1.1. Делимость и алгоритм евклида
- •1.1.1 Отношение делимости
- •1.1.2 Использование алгоритма Евклида для решения теоретико-числовых задач криптологии
- •1.1.3 Расширенный метод Евклида
- •1.2. Сравнения
- •1.2.1. Отношение сравнимости
- •1.2.2. Использование свойств сравнений для решения теоретико-числовых задач криптологии
- •Раздел 2. Криптографические системы с открытым ключом
- •2.1. Основные сведения о криптографических системах
- •2.2. Шифрование с использованием криптосистемы rsa
- •2.3. Цифровая подпись в схеме Эль-Гамаль
- •2.4. Обмен информацией с использованием протокола Шамира
- •Раздел 3. Контрольные задания
- •3.1. Программа работы
- •3.2. Примеры выполнения контрольных заданий
- •3.2.1. Шифрование с использованием криптосистемы rsa
- •3.2.2. Цифровая подпись в схеме Эль – Гамаль
- •3.2.3. Обмен информацией с использованием протокола Шамира
- •3.3. Варианты контрольных заданий
- •3.3.1. Шифрование с использованием криптосистемы rsa
- •3.3.2. Цифровая подпись в схеме Эль-Гамаль
- •3.3.3. Обмен информацией с использованием протокола Шамира
- •Библиографический список
1.2. Сравнения
1.2.1. Отношение сравнимости
Определение 11.
Для данных целых чисел![]() ,
,![]() и
и![]() ,
говорят, что
,
говорят, что![]() сравнимо с
сравнимо с![]() по модулю
по модулю![]() ,
если разность
,
если разность![]() делится на
делится на![]() :
:
|
|
|
|
При этом число
![]() называется модулем сравнения.
называется модулем сравнения.
Из определения 12 непосредственно следуют следующие свойства сравнений:
1. Рефлексивность:
|
|
|
|
2. Симметричность:
|
|
|
|
3. Транзитивность:
|
|
|
|
Таким образом,
для фиксированного значения
![]() отношение сравнимости является отношением
рефлексивным, симметричным и транзитивным,
т.е. отношением эквивалентности.
отношение сравнимости является отношением
рефлексивным, симметричным и транзитивным,
т.е. отношением эквивалентности.
В этих условиях
каждый класс эквивалентности по этому
отношению обладает в точности одним
представителем в множестве чисел от
![]() до
до![]() [9-11].
Иными словами, любое целое число сравнимо
по модулю
[9-11].
Иными словами, любое целое число сравнимо
по модулю![]() ровно с одним числом в промежутке от
ровно с одним числом в промежутке от![]() до
до![]() .
.
Множество классов
эквивалентности по модулю
![]() (называемых классами вычетов) обозначается
(называемых классами вычетов) обозначается![]() .
.
Несложно убедиться, что сравнения обладают следующим свойством [8].
4. Коммутативность
|
|
Таким образом,
множество
![]() является коммутативным кольцом, т.е.
вычет по одному и тому же модулю можно
складывать, вычитать и перемножать, и
эти операции удовлетворяют обычным
аксиомам ассоциативности, коммутативности,
существования противоположного элемента
и т.д.
является коммутативным кольцом, т.е.
вычет по одному и тому же модулю можно
складывать, вычитать и перемножать, и
эти операции удовлетворяют обычным
аксиомам ассоциативности, коммутативности,
существования противоположного элемента
и т.д.
Рассмотрим условия существования противоположного элемента.
Теорема 3. Для
каждого целого
![]() существует единственное целое число
существует единственное целое число![]() ,
такое что
произведение
,
такое что
произведение
![]() сравнимо с
сравнимо с![]() по модулю
по модулю![]() ,
тогда и только тогда, когда
,
тогда и только тогда, когда![]() и
и![]() − взаимно просты:
− взаимно просты:
|
|
|
|
Схема доказательства:
Для доказательства теоремы необходимо
представить
![]() в виде
в виде![]() и воспользоваться теоремой 2 и свойствами
сравнений [15].
и воспользоваться теоремой 2 и свойствами
сравнений [15].
Следствие: Если
![]() то обратный элемент
то обратный элемент![]() (из условия
(из условия![]() )
может быть найден за время
)
может быть найден за время![]() двоичных операций.
двоичных операций.
Замечание: Если
![]() ,
то под отрицательной степенью
,
то под отрицательной степенью![]() подразумевается
подразумевается![]() -я
степень обратного класса вычетов, т.е.
класс вычетов, содержащий
-я
степень обратного класса вычетов, т.е.
класс вычетов, содержащий![]() -ю
степень любого целого числа
-ю
степень любого целого числа![]() ,
такого, что
,
такого, что![]() .
.
1.2.2. Использование свойств сравнений для решения теоретико-числовых задач криптологии
Подробное рассмотрение свойств сравнений позволяет получить следующий важный результат [8,9].
Теорема 4 (малая
теорема Ферма). Пусть
![]() − простое число. Любое целое число
− простое число. Любое целое число![]() удовлетворяет сравнению
удовлетворяет сравнению![]() ,
и любое целое число
,
и любое целое число![]() ,
не делящееся на
,
не делящееся на![]() ,
удовлетворяет сравнению
,
удовлетворяет сравнению![]() .
.
Из условий данной теоремы несложно получить следствие.
Следствие. Если
![]() не делится на
не делится на![]() и если
и если![]() ,
то
,
то![]() .
.
Пример 6. Найти
последнюю цифру в записи числа
![]() в системе счисления по основанию 7.
в системе счисления по основанию 7.
Решение: Пусть
![]() ,
т.к.
,
т.к.![]() ,
то
,
то
![]() .
Следовательно, последняя цифра равна
2.
.
Следовательно, последняя цифра равна
2.
Не менее важное свойство сравнений отражает т.н. китайская теорема об остатках.
Теорема 5 (китайская теорема об остатках). Пусть требуется решить систему сравнений по различным модулям:
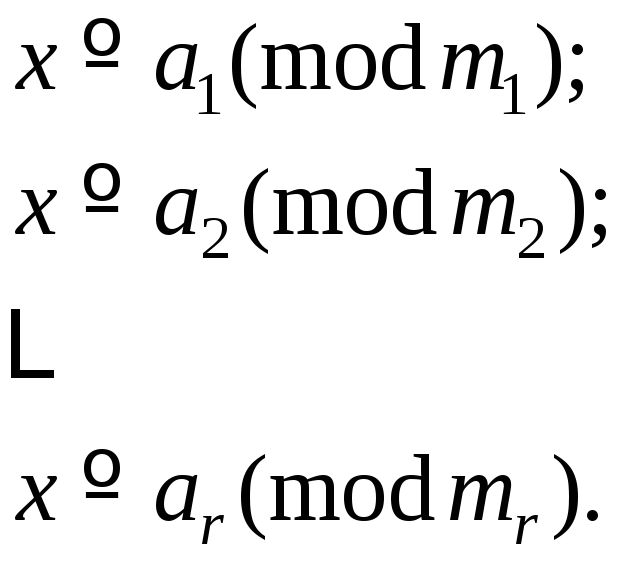
причем любые два
модуля сравнения взаимно просты
относительно друг друга:
![]() .
Тогда эта система разрешима, и любые
два решения сравнимы по модулю
.
Тогда эта система разрешима, и любые
два решения сравнимы по модулю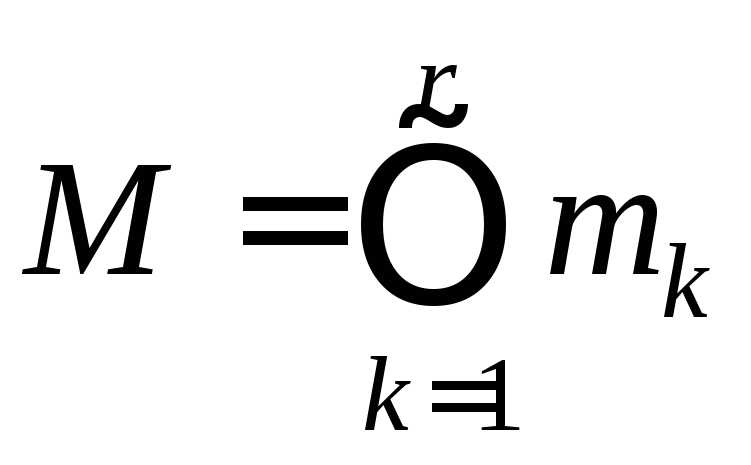 .
.
Данная теорема позволяет сформулировать следующее важное следствие.
Следствие. Функция Эйлера обладает свойством «мультипликативности», т.е.
![]() .
.
Теорема 6. Пусть
известно, что
![]() есть произведение двух простых чисел
есть произведение двух простых чисел![]() и
и![]() .
Тогда зная эти числа
.
Тогда зная эти числа![]() и
и![]() ,
можно найти
,
можно найти![]() за время порядка
за время порядка![]() и
обратно, зная
и
обратно, зная![]() и
и![]() ,
можно найти
,
можно найти![]() и
и![]() за время порядка
за время порядка![]() .
.
Доказательство. Утверждение
очевидно, если
![]() − четно, т.к. в этом случае
− четно, т.к. в этом случае![]() ,
,![]() и
и![]() ;
поэтому рассмотрим случай когда
;
поэтому рассмотрим случай когда![]() −
нечетно. В силу мультипликативности
функции Эйлера для
−
нечетно. В силу мультипликативности
функции Эйлера для![]() получаем
получаем![]() .
Таким образом, значение
.
Таким образом, значение![]() может быть получено с помощью одного
сложения и одного вычитания.
может быть получено с помощью одного
сложения и одного вычитания.
Обратно, предположим,
что известны
![]() и
и![]() ,
и требуется найти
,
и требуется найти![]() и
и![]() .
Для неизвестных величин
.
Для неизвестных величин![]() и
и![]() известны их произведение
известны их произведение![]() и сумма
и сумма![]() .
Обозначим последнее выражение через
.
Обозначим последнее выражение через![]() (отметим,
(отметим,![]() — число четное). Но два числа, произведение
которых равно
— число четное). Но два числа, произведение
которых равно![]() ,
а сумма
,
а сумма![]() ,
по теореме Виета должны быть корнями
квадратного уравнения
,
по теореме Виета должны быть корнями
квадратного уравнения![]() .
Итак
.
Итак![]() и
и![]() равно
равно![]() .
Наибольшее время при вычислении занимает
процедура извлечения квадратного корня:
на нее требуется
.
Наибольшее время при вычислении занимает
процедура извлечения квадратного корня:
на нее требуется![]() двоичных операций [9].
двоичных операций [9].
Рассмотрим обобщение малой теоремы Ферма, сделанное Эйлером.
Теорема 7 (теорема Эйлера).
![]() .
.
Схема доказательства.
Для начала
необходимо доказать справедливость
утверждения для случая, когда
![]() есть степень простого числа:
есть степень простого числа:![]() .
Выполняя индукцию по
.
Выполняя индукцию по![]() ,
при
,
при![]() ,
получаем малую терему Ферма. Рассматривая
биномиальные коэффициенты в выражении
,
получаем малую терему Ферма. Рассматривая
биномиальные коэффициенты в выражении![]() ,
получаем доказательство частного
случая.
,
получаем доказательство частного
случая.
В дальнейшем, используя мультипликативность функции Эйлера и тот факт, что степени различных простых чисел взаимно просты, доказывается и общий случай [12-14].
Следствие. Если
![]() и
и![]() — наименьший неотрицательный вычет
— наименьший неотрицательный вычет![]() по модулю
по модулю![]() ,
то
,
то![]() .
.
Пример 7. Вычислить
![]() .
.
Решение:
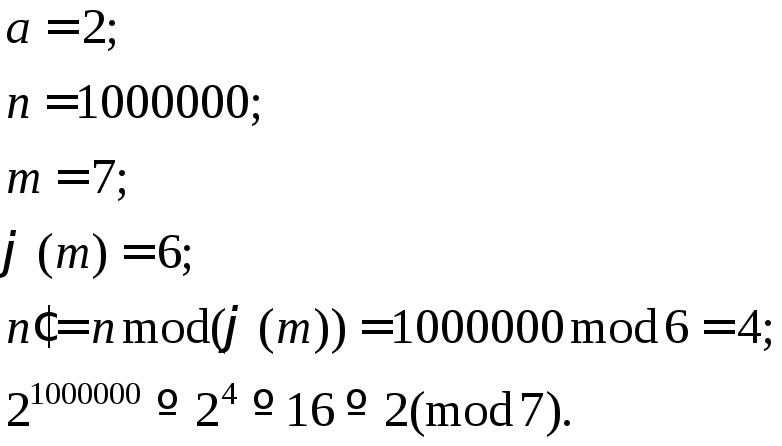
{ Расширенный алгоритм Евклида }
Упражнения для самоконтроля
Решить систему сравнений:

Найти последнюю цифру в записи числа
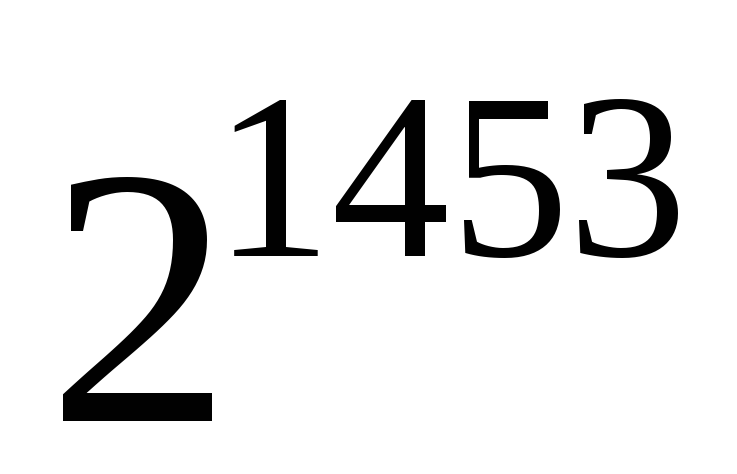 в системе счисления по основанию 11.
в системе счисления по основанию 11.Вычислить
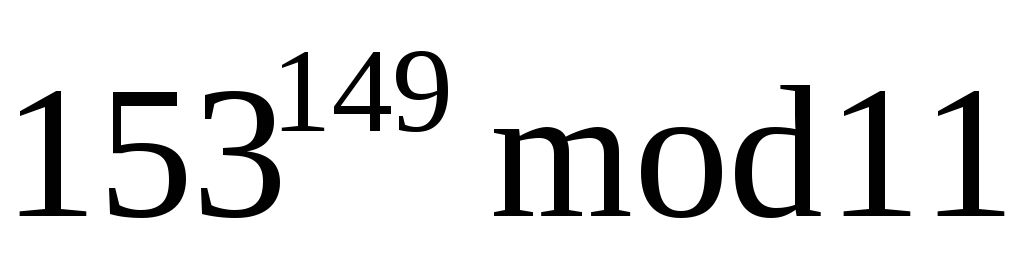 .
.Вычислить
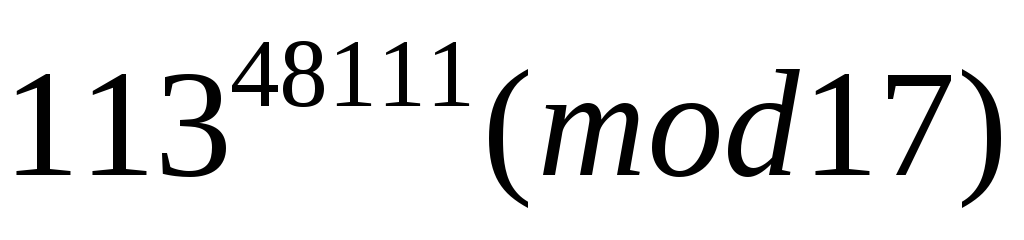 .
.