Практическое занятие № 9 Тема: «Способы задания плоскости»

Примеры решения задач.

Пример 1.

Даны точки . Составить уравнение плоскости, проходящей через точку, перпендикулярно вектору.

Решение.

Будем искать уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору:

где - нормальный вектор плоскости, - координаты точки, принадлежащей плоскости.

В качестве точки можно выбрать любую из данных точек, например, точку

.

В качестве нормального вектора выбираем вектор .

Тогда уравнение плоскости принимает вид:

Пример 2.

Найти отрезки, отсекаемые плоскостью на осях координат.

Решение.

Уравнение плоскости в отрезках, отсекаемых ею на осях координат имеет вид:

где a, b, с – отрезки, отсекаемые плоскостью на осях координат.

В нашем случае плоскость задана общим уравнением. Нужно привести его к виду плоскости в отрезках. Для этого перенесем свободный член в правую часть:

И разделим обе части уравнения на (-6):

Отсюда находим

Пример 3.

Составить уравнение плоскости, проходящей через точки .

Решение.

Используем уравнение плоскости, проходящей через три точки:

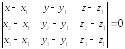
Подставляем в это уравнение координаты заданных точек:

Пример 4.

Найти уравнение плоскости, проходящей через точку параллельно плоскости.

Решение.

Будем искать уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору. В качестве точки, принадлежащей плоскости, берем точку .

Так как искомая плоскость параллельна плоскости , то у них будет один и тот же нормальный вектор. Поэтому в качестве нормального вектора выбираем нормальный вектор заданной плоскости:

Имеем:

Отметим, что, поскольку у параллельных плоскостей совпадают нормальные вектора, то у них в общем уравнении плоскости получаются одинаковые коэффициенты при х, y, z.

Пример 5.

Найти уравнение плоскости, параллельной плоскости и отстоящей от нее на расстояние, равное 5.

Решение.

Так как плоскости параллельны, то коэффициенты общего уравнения плоскости у них совпадают, поэтому уравнение искомой плоскости можно записать в виде

Таким образом, задача сводится к нахождению свободного члена D. Воспользуемся формулой расстояния от точки до плоскости:

.

где - координаты точки, от которой мы ищем расстояние, А, В, С – коэффициенты общего уравнения плоскости, до которой мы ищем это расстояние. Причем, это расстояние по условию задачи нам известно и равно 5. Коэффициенты нам известны:

Осталось найти координаты точки, принадлежащей заданной плоскости .

Для этого выберем две координаты произвольно, а третью найдем из уравнения. Например, пусть , тогда. Подставляем в формулу расстояния от точки до плоскости:

Таким образом, у нас получилось две плоскости, которые параллельны заданной плоскости и отстоят от нее на заданное расстояние:

Пример 6.

Составить уравнение плоскости, проходящей через точку 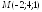, параллельно плоскости, проходящей через точки.

Решение.

Сначала найдем уравнение второй плоскости, которая проходит через три заданные точки. Для этого используем уравнение плоскости, проходящей через 3 точки.

Таким образом, искомая плоскость параллельна плоскости , следовательно, далее задача сводится к решению задачи 4.

Будем искать уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору. В качестве точки, принадлежащей плоскости, берем точку .

Так как искомая плоскость параллельна плоскости , то у них будет один и тот же нормальный вектор. Поэтому в качестве нормального вектора выбираем нормальный вектор заданной плоскости:

Имеем:

Пример 7.

Найти угол между плоскостямии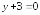

Решение.

Угол между плоскостями - это угол между нормальными векторами этих плоскостей. Нормальные вектора данных плоскостей:

и .

По формуле угла между двумя векторами:

Пример 8.

Составить уравнение плоскости, проходящей через точки , параллельно вектору.

Решение.

Будем искать уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору.

В качестве точки можно выбрать любую из данных точек, например, точку .

Остается найти нормальный вектор к искомой плоскости. Его можно найти как векторное произведение двух направляющих векторов:

.

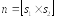Один направляющий вектор у нас задан: . Второй направляющий вектор найдем как вектор (поскольку он лежит в искомой плоскости). Тогда

Следовательно, нормальный вектор будет иметь координаты: .

Тогда уравнение плоскости принимает вид:

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:

1. Даны точки . Составить уравнение плоскости, проходящей через точкуперпендикулярно вектору.

2. Найти уравнение плоскости, проходящей через точки А(1,1,1), В(0,-1,2) и С(2,3,-1).

3. Найти расстояние между параллельными плоскостями: 4х-2у+4z+5=0 и 2х-у+2z-7=0.

4. Найти расстояние от точки А(5,1,-1) до плоскости х-2у-2z+4=0.

5. Составить уравнение плоскости, проходящей через начало координат и точку М(2,1,-1) перпендикулярно плоскости 2х-3z=0.

6. Найти уравнение плоскости, проходящей через точки перпендикулярно плоскости –х+у-1=0.

7. Составить уравнение плоскости, проходящей через точку М(-2,3,1) параллельно плоскости ХОУ.

8. Найти отрезки, отсекаемые плоскостью на осях координат.

9. Найти угол между плоскостями 2х-4у+4z-3=0 и х-3у+z=0.

10. Найти длину перпендикуляра, опущенного из начала координат на плоскость 20х-5у+4z-210=0.

11. Найти уравнение плоскости, параллельной плоскости х+2у-3z-2=0 и отстоящей от нее на расстояние, равное 2.