
- •О.И.Тутынина
- •Содержание
- •Пояснительная записка
- •Перечень практических работ
- •Практическое занятие № 1 Тема: «Линейные операции над матрицами. Произведение матриц. Транспонирование»
- •Практическое занятие № 2 Тема: «Определитель матрицы. Обратная матрица»
- •Практическое занятие № 3 Тема: «Решение систем линейных уравнений»
- •Практическое занятие № 4 Тема: «Решение систем линейных уравнений методом Гаусса»
- •Практическое занятие № 5 Тема: «Линейные операции над векторами. Скалярное произведение векторов»
- •Практическое занятие № 6 Тема: «Векторное и смешанное произведения векторов»
- •Практические занятия № 7, № 8 Тема: «Способы задания прямой на плоскости»
- •Практическое занятие № 9 Тема: «Способы задания плоскости»
- •Практическое занятие № 10 Тема: «Способы задания прямой в пространстве»
- •Практическое занятие № 11 Тема: «Взаимная ориентация прямой и плоскости»
- •Практическое занятие № 12 Тема: «Преобразование кривых второго порядка»
- •Список литературы
Практическое занятие № 3 Тема: «Решение систем линейных уравнений»
Примеры решения задач.
Пример 1.
Решить систему уравнений тремя способами.

Решение:
1 способ: метод Гаусса.
Составляем расширенную матрицу системы, в которую входят коэффициенты при переменных и свободные члены:

Чтобы
исключить переменную
 из второго и третьего уравнений, умножим
первую строку на (-2) и (-3) и полученные
строки прибавим ко второй и третьей
строке соответственно:
из второго и третьего уравнений, умножим
первую строку на (-2) и (-3) и полученные
строки прибавим ко второй и третьей
строке соответственно:

Чтобы
исключить переменную
 из третьего уравнения, умножим вторую
строку на (-1) и полученную строку прибавим
к третьей строке:
из третьего уравнения, умножим вторую
строку на (-1) и полученную строку прибавим
к третьей строке:

Получили систему уравнений, равносильную исходной системе, в которой первое уравнение содержит три переменных, второе – две, а третье – одну переменную:

Отсюда последовательно находим:

Таким образом, решение системы:
 .
.
Проверяем полученное решение, подставляя найденные значения в исходную систему:

Получили тождественные равенства, следовательно система решена правильно.
Второй способ: метод Крамера.
Составляем матрицу системы:

Вычисляем определитель этой матрицы:

Находим
определители
 ,
получающиеся из исходного определителя
заменой соответственно первого, второго
и третьего столбцов столбцом свободных
членов:
,
получающиеся из исходного определителя
заменой соответственно первого, второго
и третьего столбцов столбцом свободных
членов: .
.

Теперь
используя формулы Крамера
 ,
находим решение системы:
,
находим решение системы:

Третий способ: метод обратной матрицы.
Запишем
матрицу системы
 и матрицу-столбец свободных членов
и матрицу-столбец свободных членов .
.
Определитель
матрицы А был найден ранее:
 .
.
Найдем матрицу, обратную к матрице А. Для этого составляем матрицу из алгебраических дополнений элементов определителя матрицы А и транспонируем ее:
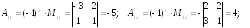



Полученную матрицу делим на определитель исходной матрицы и записываем обратную матрицу:

Решением
исходной системы уравнений будет
матрица-столбец
 ,
найденная как произведение обратной
матрицы на матрицу-столбец свободных
членов:
,
найденная как произведение обратной
матрицы на матрицу-столбец свободных
членов:
 .
.
Таким образом:

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
1.Решить системы линейных уравнений:

Практическое занятие № 4 Тема: «Решение систем линейных уравнений методом Гаусса»
Примеры решения задач.
Пример 1.
Решить систему методом Гаусса:

Решение:
Дана неоднородная система 4 линейных уравнений с 4 неизвестными. Решаем ее методом Гаусса. Составляем расширенную матрицу:

Получим три нуля в первом столбце, два нуля – во втором и один ноль – в третьем. Для этого сначала третью строку умножим на (-2) и сложим с первой строкой, затем вторую строку умножим на (-2) и (-3) и сложим с первой и четвертой строками соответственно. И, наконец, первую строку умножим на (-7) и сложим с четвертой строкой:

Переходим к системе уравнений:

Отсюда находим:

Пример 2.
Решить систему методом Гаусса:

Решение:
Дана неоднородная система 4 линейных уравнений с 5 неизвестными. Решаем ее методом Гаусса. Составляем расширенную матрицу и преобразуем ее:

Третья и
четвертая строки противоречат друг
другу, поскольку им соответствуют
уравнения
 .
Поэтому система несовместна и решения
не имеет.
.
Поэтому система несовместна и решения
не имеет.
Пример 3.
Решить систему методом Гаусса:

Решение:
Дана неоднородная система 3 линейных уравнений с 4 неизвестными. Решаем ее методом Гаусса. Составляем расширенную матрицу и преобразуем ее:

Переходим к системе уравнений:

Таким образом,
система совместна и неопределенна,
имеет бесконечное множество решений.
Переменные
 являются базисными, а переменная
являются базисными, а переменная - свободной.
- свободной.
Пример 4.
Решить систему методом Гаусса:

Решение:
Дана однородная система 3 линейных уравнений с 3 неизвестными. Отметим, что однородные системы всегда являются совместными, поскольку для них всегда есть тривиальное нулевое решение. Поэтому остается выяснить, будет ли это решение единственным, или же решений будет бесконечно много. Составляем расширенную матрицу и преобразуем ее:

Отметим, что получились две одинаковые строки, одну из которых можно убрать. Переходим к системе уравнений:

Система
совместна и неопределенна, имеет
бесконечное множество решений. Переменные
 являются базисными, а переменная
являются базисными, а переменная - свободной.
- свободной.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
1.Решить системы линейных уравнений методом Гаусса:
1. 2.
2. 3.
3.
4. 5.
5.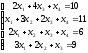 6.
6.
7. 8.
8.
