Лекция 10 Методы локальной пользовательской маршрутизации Алгоритм Дейкстры

Эти методы обеспечивают оптимальный маршрут прохождения пакета между отдельной парой абонентов. Введем обозначения: D(v) – суммарная стоимость минимального пути от источника (узел с номером 1) до получателя (узел с номеромv),l(i,j) – стоимость канала от узлаiдо узлаj. Определена только для смежных узлов. Для несмежных равна. Это подход является алгоритмом Дейкстры для сетевой маршрутизации.

Шаг0. Строится множествоN, содержащее номер одного узла (первого). Строится таблица: строки таблицы – итерации, столбцы – номер операции, множествоN, номера узлов (начиная со второго). В строке для нулевой итерации, в столбце для узлаvфиксируется значениеD₁(v) =l(1,v). Нижний индекс показывает номер узла, через который достигается текущее оптимальное значение. Строиться корень дерева с узлом 1.

Шаг k (k = 1,2,3,…). В текущей строке выбираем узелvтакой, что он не из множестваN, но является смежным с каким-либо из узлов множестваNи такой, что значениеD_p(v) минимально. Узелvвключается во множествоN. В дереве добавляется узел с номеромvв качестве потомка узла с номеромp. Далее формируется новая строка таблицы, делается пересчет. Для всех узловwNпроверяем, изменилось ли стоимость маршрута по следующему правилу: ,w* – любое,, если было оставлено старое значение,иначе.

Алгоритм заканчивает работу, исчерпав все множество вершин.

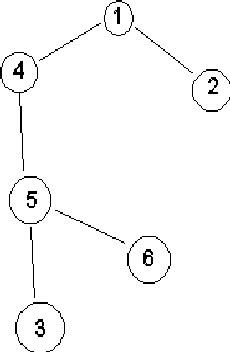
Пример:

	Nитер	N	2	3	4	5	6
	0	1	21	51	11	1	1
	1	1, 4	21	44	11	24	45
	2	1, 4, 2	21	35	11	24	45
	3	1, 4, 2, 5	21	35	11	24	45
	4	1, 4, 2, 5, 3	21	35	11	24	45
	5	1, 4, 2, 5, 3, 6

Получатель	Смежный
2	2
3	4
4	4
5	4
6	4

Получено решение (маршрутная таблица) для узла с номером 1. Эта таблица расчитывается для каждого узла отдельно. Алгоритм может быть реализован самостоятельно каждым узлом. Недостатком является необходимость информации о стоимости всех каналов сети.

Подход Форда-Фолкирсона

Каждому узлу пристваивается метка (N,D(v)), гдеD(v) – текущая величина минимального расстояния от узлаvдо получателя (узел 1), иN– смежный сvузел, через который достигнуто это минимальное расстояние.

Шаг0. Строим таблицу, где первый столбец – номер итерации, остальные – номера узлов. Формируем первую строку: (1,l(v,1)) для узловv, которые смежны с узлом 1. Для узлов, несмежных с 1 (,).

Шаг k (k = 1,2,…). Пересчет строки таблицы.

Алгоритм заканчивает работу, если в текущей итерации не была изменена ни одны метка.

Пример:

		1	2	3	4	5	6
	0	(1,0)	( ,)	( ,)	( ,)	( ,)	( ,)
	1	(1,0)	(1,2)	(1,5)	(1,1)	(4,2)	(5,4)
	2	(1,0)	(1,2)	(5,3)	(1,1)	(4,2)	(5,4)
	3	(1,0)	(1,2)	(5,3)	(1,1)	(4,2)	(5,4)

Замечание. Алгоритм Дейкстра может быть выполнен децентрализованно. Но при этом должны быть известны стоимости всех каналов связи в каждом узле. Т.к. в реальных сетях эта величина динамически меняется, то более эффективно выполнять расчет централизованным способом. Алгоритм Форда-Фолкирсона не может быть выполнен децентрализованно, т.к. там расчитываются все маршрутные таблицы. Однако именно он послужил основой для полностью децентрализованного алгоритма, использовавшегося вARPANet, который в настоящее время является основой дляInternet.

5.