
Радиоприемные устройства
.docxРадиоприемные устройства
Задача 1.
Определить полосу пропускания контура входной цепи на уровне γ=0,5, если избирательность контура по соседнему каналу σе ск=3. Частота соседнего канала отличается от частоты сигнала на величину ∆f= 2 МГц.
Дано:
γ=0,5
σе ск=3
∆f= 2 МГц.
Пγ-?
Решение:
Полоса пропускания при заданной неравномерности определяется так:
Пγ=f0dэ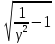 ,
где
dэ-эквивалентное
затухание контура,
,
где
dэ-эквивалентное
затухание контура,
f0-резонансная частота
резонансную частоту и эквивалентное затухание найдем из формулы избирательности по соседнему каналу:
σе
ск=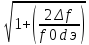 2,
⟶
f0dэ=
2,
⟶
f0dэ=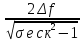
Подставим в формулу полосы пропускания:
Пγ=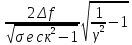
Пγ=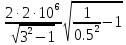 =1.41·
=1.41·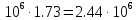 ,
Гц
,
Гц
Ответ: Пγ=2,44 МГц.
Задача 2.
Определить избирательность по зеркальному каналу входной цепи с резонансной частотой 100 МГц, если известно, что полоса пропускания на уровне 0,6 составляет 2 МГц, а частота гетеродина 110 МГц.
Дано:
f0=100 МГц
Пγ=2 МГц
γ=0,6
fг= 110 МГц
σе зк -?
Решение:
Избирательность входной цепи можно рассчитать по формуле:
σе
зк= ,
где ξ-
обобщенная расстройка контура.
,
где ξ-
обобщенная расстройка контура.
ξ=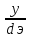 ,
где
y-
относительная расстройка,
,
где
y-
относительная расстройка,
dэ-эквивалентное затухание контура.
y=
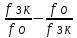 ,
где
fзк
– частота зеркального канала,
,
где
fзк
– частота зеркального канала,
найдем частоту зеркального канала из формулы:
fзк= f0+2fпр, где fпр- промежуточная частота, выразим fпр:
fпр=fг-f0,
эквивалентное затухание можно определить из формулы полосы, при заданной неравномерности:
Пγ=f0dэ ,
⟶
dэ
=
,
⟶
dэ
=
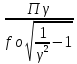
dэ
=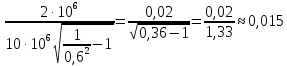 ,
,
fпр=110·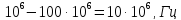
fзк=100+2·10·
y=
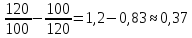
ξ=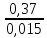 ≈24,7,
≈24,7,
σе
зк=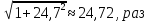
σе зк = 20log24.72=27.86 , дБ
Ответ: σе зк=24,72 или σе зк дБ=27.86 дБ
Задача 3.
Определить коэффициенты перекрытия диапазона входной цепи, если избирательность по соседнему каналу на границах диапазона 1,3 дБ и 2,6 дБ, а эквивалентные затухания при перестройке не изменяются.
Дано:
σе зк н= 1,3 дБ
σе зк в= 2,6 дБ
dэ=const
kд-?
Решение:
коэффициент перекрытия диапазона входной цепи можно рассчитать по формуле:
kд=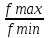 ,
где fmin
и
fmax
–
это границы диапазона входной цепи
,
где fmin
и
fmax
–
это границы диапазона входной цепи
(fmin=fн, fmax=fв)
Для того, чтобы найти fн и fв воспользуемся формулой
избирательности по соседнему каналу:
σе
ск=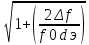 2
, → σ2е
ск
-1 =
2
, → σ2е
ск
-1 =
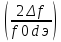 2,
2,
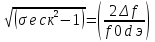 2,
f0=
2,
f0=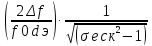
Как видно, с ростом частоты избирательность уменьшается, значит, для верхней частоты соответствует меньшее значение избирательности, а для нижней частоты- большее:
fн=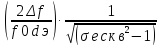 ,
fв=
,
fв=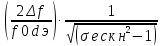 ,
,
→ kд=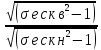
Рассчитаем kд, подставив соответствующие значения избирательности:
σе
зк в(раз)=102,6/20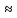 1,34,
σе
зк н(раз)=101,3/20
1,34,
σе
зк н(раз)=101,3/20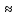 1,16
1,16
kд=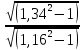 =
= ≈1,5
≈1,5
Ответ: kд=1,5
Задача 4.
Чему равно максимальное значение крутизны транзисторного преобразователя частоты, если под действием напряжения гетеродина крутизна меняется по гармоническому закону и ее минимальное значение Sмин = 10 мА/В. Резонансный коэффициент усиления преобразователя равен 10, эквивалентное резонансное сопротивление Rэ=2 кОм, коэффициенты включения контура m=1, n=0,5
Дано:
Sмин = 10 мА/В
Rэ=2 кОм
m=1
n=0,5
k0=10
Sмакс-?
Решение:
Из формулы резонансного коэффициента усиления преобразователя:
k0=mnSпрRэ, где Sпр- крутизна преобразования
Sпр=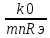 ,
,
Для нахождения крутизны преобразования есть формула:
Sпр=0,25(Sмакс- Sмин), выразим из нее Sмакс:
Sмакс=
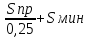
Sпр=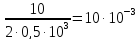 ,
А/В
,
А/В
Sмакс=
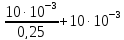 =50·10-3,
А/В
=50·10-3,
А/В
Ответ: Sмакс=50 мА/В
Задача 5.
Определить амплитуду тока промежуточной частоты на выходе преобразователя частоты при короткозамкнутой нагрузке, если крутизна характеристики транзистора линейно зависит от Sмин=0,02 А/В до Sмакс=0,1 А/В. Амплитуда входного сигнала Uс=100 мкВ.
Дано:
Sмин=0,02 А/В
Sмакс=0,1 А/В
Uс=100 мкВ
Iпр-?
Решение:
Воспользуемся обратным уравнением преобразования:
Iпр= Y21 пр Uc + Y22 Uпр, где Y21 пр- крутизна преобразования (Y21 пр=Sпр),
Y22 Uпр=0, т.к. на выходе преобразователя короткое замыкание.
Найдем крутизну преобразования по формуле:
Sпр=0,25(Sмакс- Sмин),
Sпр=0,25(0,1-0,02)=0,02 А/В
Iпр=0,02·100·10-6=2·10-6, А
Ответ: Iпр=2 мкА
Задача 6.
Рассчитайте амплитуду напряжения гетеродина, при которой амплитуда составляющей тока с промежуточной частотой на выходе транзисторного преобразователя частоты в режиме короткого замыкания нагрузки равна Iпч=3 мкА, если амплитуда входного сигнала Uc=100 мкВ и вольтамперная характеристика транзистора описывается выражением i2=i20+aΔU+b ΔU2, в котором b=0.3 А/В2.
Дано:
Iпч=3 мкА
Uc=100 мкВ
i2=i20+aΔU+b ΔU2
b=0.3 А/В2
Uг-?
Решение:
Из формулы крутизны преобразования :
Y21
пр=bUг,
выразим амплитуду напряжения гетеродина
Uг=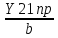 =
=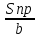
Воспользуемся уравнением преобразования:
Iпр= Y21 пр Uc, где Iпр - амплитуда тока промежуточной частоты→
Y21
пр= ,
Y21
пр=
,
Y21
пр=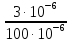 =0,03,
А/В
=0,03,
А/В
Uг=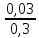 =0,1
, В
=0,1
, В
Ответ: Uг=0,1 В
Задача 7.
Определить частоту модуляции сигнала на входе диодного детектора, при которой искажение из-за инерционности нагрузки детектора RнСн и из-за разделительной цепи Rу Ср возникает при одном и том же коэффициенте амплитудной модуляции сигнала. Сопротивление Rн =10 кОм, Rу= 40 кОм и Сн= 500 пФ.

Дано:
Rн =10 кОм
Rу= 40 кОм
Сн= 500 пФ
Fв-?
Решение:
Искажения из-за нелинейности детекторной характеристики будут отсутствовать при условии, что
Um0≥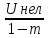 ,
где Uнел
– величина нелинейного участка,
,
где Uнел
– величина нелинейного участка,
Um0- амплитуда несущей на входе детектора
m- глубина модуляции
при условии неискаженного сигнала из-за инерционности
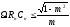 ,
где
Ω- модулирующая частота
,
где
Ω- модулирующая частота
Ω=2πf,
→ Fв
=
Из условия малых нелинейных искажений из-за разделительной цепи:
Rн≤ Rу,
найдем m
Rу,
найдем m
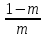 ≥
≥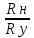 ,
,
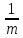 -1≥
-1≥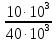 ,
,
 ≥
0,25+1, m
≥
≥
0,25+1, m
≥
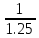 ,
m≥0.8
,
m≥0.8
Fв=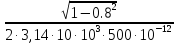 =
=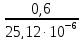 =23,9·103,
Гц
=23,9·103,
Гц
Ответ: Fв =23.9 кГц
Задача 8
Определить сопротивление нагрузки Rн диодного детектора, при котором искажение из-за нелинейности начального участка характеристики детектирования и из-за разделительной цепи Ry Cр наступают при одном и том же коэффициенте амплитудной модуляции входного сигнала.Uвх=1В, протяженность нелинейного участка характеристики Uнел. =0.1В.и сопротивление Rф= 90кОм .

Дано:
Uнел. =0.1В
Uвх=1В
Rф= 90кОм
Rн -?
\
Решение:
Искажения из-за нелинейности детекторной характеристики будут отсутствовать при условии, что
Um0≥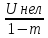 ,
где Uнел
– величина нелинейного участка,
,
где Uнел
– величина нелинейного участка,
Um0- амплитуда несущей на входе детектора
m- глубина модуляции
1-m≥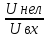
из характеристики диода
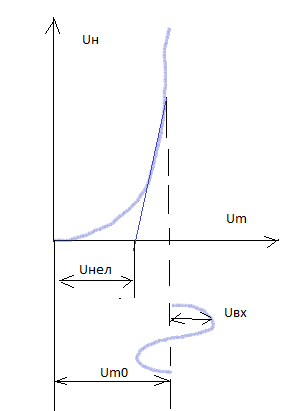 Um0=
Uнел+
Uвх
Um0=
Uнел+
Uвх
Uвх=1+0,1=1,1 В
1-m
≥
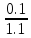 ,
m≤
0.9
,
m≤
0.9
Из условия малых нелинейных искажений из-за разделительной цепи:
Rн≤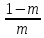 Rу
,
Rу
,
Rн
=
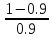 ·90·103
= 10·103
, Ом
·90·103
= 10·103
, Ом
Ответ: Rн=10 кОм
Задача 9
Определите амплитуду сигнала на входе диодного детектора, при которой искажения из-за нелинейности начального участка характеристики детектирования и из-за разделительной цепи RуCр возникают при одном и том же коэффициенте амплитудной модуляции входного сигнала, если протяженность нелинейного участка равна Uнел=0,1 В, Rн=10 кОм и Rу= 40 кОм.
Дано:
Uнел=0,1 В
Rн=10 кОм
Rу= 40 кОм
Uвх-?
Решение:
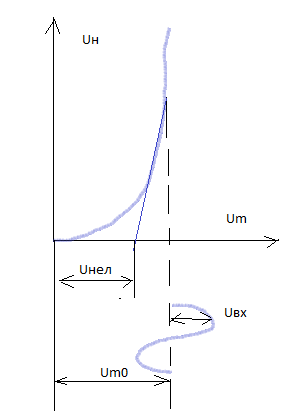
Искажения из-за нелинейности детекторной характеристики будут отсутствовать при условии, что
Um0≥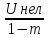 ,
где Uнел
– величина нелинейного участка,
,
где Uнел
– величина нелинейного участка,
Um0- амплитуда несущей на входе детектора
m- глубина модуляции
Um0= Uнел+ Uвх, из характеристики диода
Из условия малых нелинейных искажений из-за разделительной цепи:
Rн≤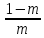 Rу
, →
Rу
, →
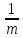 -1≥
-1≥
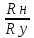 ,
,
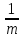
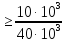 +1 m≥
+1 m≥
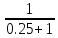 , m≥0.8
, m≥0.8
Um0≥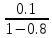 ,
Um0≥0,5
В
,
Um0≥0,5
В
Uвх= Um0- Uнел=0,5-0,1=0,4 В
Ответ: Uвх=0,4 В
Задача 10.
Определить резонансную частоту f0, при которой неравномерность коэффициента передачи в полосе пропускания контура равна γ1=0,9, если при частоте f01=1 МГц, неравномерность γ=0,6 . Эквивалентное затухание контура на разных частотах считать одинаковыми.
Дано:
f01=1 МГц
γ1=0,6
γ=0,9
f0-?
Решение:
воспользуемся формулой полосы пропускания при заданной неравномерности:
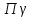 =f0dэ
=f0dэ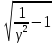 ,
где
dэ-эквивалентное
затухание контура
,
где
dэ-эквивалентное
затухание контура
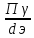 =
f0
=
f0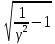 ,
при
f01=1
МГц и γ1=0,6:
,
при
f01=1
МГц и γ1=0,6:
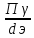 =
106·
=
106·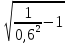 ≈1,3
·106,
Гц
≈1,3
·106,
Гц
Найдем f0:
f0=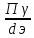 ·
·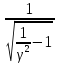 ,
f0=1,3·106·
,
f0=1,3·106·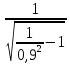 =
0,64·106
Гц
=
0,64·106
Гц
Ответ: f0= 0,64 МГц
Задача 11.
Определить коэффициенты включения mc и nc в одноконтурной входной цепи, обеспечивающие согласование настроенной антенны со входом приемника при требуемой полосе пропускания П=37,5 МГц, если f0=150 МГц, Ra=100 Ом, Ck=20 пФ, dk=0.05, Rвх=500 Ом.
Дано:
П=37,5 МГц
f0=150 МГц
Ra=100 Ом
Ck=20 пФ
dk=0.05
Rвх=500 Ом
mc -? nc -?
Решение:
Для вычисления коэффициентов трансформации, обеспечивающих согласование настроенной антенны используются следующие формулы:
mc=
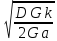 , nc=
, nc=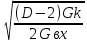 ,
где D-коэффициент
затухания,
,
где D-коэффициент
затухания,
Gk-проводимость контура, Gа- проводимость антенны, Gвх- входная проводимость
Найдем все неизвестные.
D=
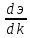 ,
где dэ
– эквивалентное затухание контура.
,
где dэ
– эквивалентное затухание контура.
Дя нахождения dэ воспользуемся формулой полосы пропускания при заданной неравномерности. Считаем на уровне 0,707, тогда
П0,707=f0dэ,
→
dэ=
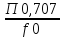 ,
dэ=
,
dэ=
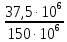 =
0,25
=
0,25
D
=
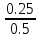 =5
=5
Проводимость контура обратна величине сопротивления контура:
Gk=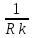 , Rк
=ρ·Qk,
где ρ- характеристическое сопротивление
контура,
, Rк
=ρ·Qk,
где ρ- характеристическое сопротивление
контура,
Qk- добротность контура
Qk
=
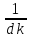 , ρ
=
, ρ
=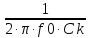 ,
→ Rk
=
,
→ Rk
=
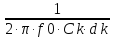 ,
,
Rk
=
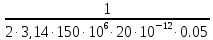 =1.1·103
, Ом
=1.1·103
, Ом
Gk=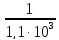 =0,94
·
10-3
А/В
=0,94
·
10-3
А/В
Проводимость антенны обратна величине сопротивления антенны:
Gа=
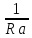 , Gа=
, Gа=
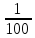 =
0,01 А/В
=
0,01 А/В
Входная проводимость обратна величине входного сопротивления:
Gвх=
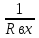 ,
Gвх=
,
Gвх=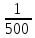 =
0,002 А/В
=
0,002 А/В
mc
=
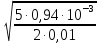 ≈
0,5
≈
0,5
nc
=
 ≈0,84
≈0,84
Ответ: mc =0,5 , nc≈ 0,84
Задача 12.
Резонансный коэффициент усиления каскада 30 достигается при крутизне характеристики транзистора 80 мА/В. Эквивалентное затухание контура 0,04, емкость 1000 пФ, коэффициенты включения m=0.5 и n=0.2. Определить, на какую частоту настроен контур.
Дано:
k0 = 30
S = 80 мА/В
dэ =0,04
Ск= 1000 пФ
m=0.5
n=0.2
f0-?
Решение:
Воспользуемся формулой резонансного коэффициента усиления:
k0 = mnSRэкв , где Rэкв-эквивалентное сопротивление контура
Rэкв =ρQэ, Qэ –эквивалентная добротность,
ρ- характеристическое сопротивление контура
Qэ
=
 ,
ρ =
,
ρ =
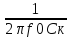 →
→
f0
=

из формулы резонансного коэффициента усиления выразим Rэкв
Rэкв
= ,
Rэкв
=
,
Rэкв
=
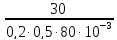 =
3,75 · 103,
Ом
=
3,75 · 103,
Ом
ρ
=
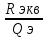 = Rэкв
· dэ
, → f0
=
= Rэкв
· dэ
, → f0
=
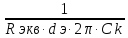
f0
=
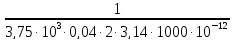 =
=
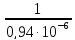 = 1,06 ·106
, Гц
= 1,06 ·106
, Гц
Ответ: f0 = 1,06 МГц
Задача 13.
Рассчитать разделительную емкость в однокаскадном УЗЧ, если входное сопротивление Rвх=470 кОм, сопротивление нагрузки Rн=10 кОм, а частотные искажения Мн, допустимые на весь усилитель на нижней частоте 30 Гц, не более 6 дБ. Частотные искажения распределить поровну между емкостями. Выходное сопротивление усилителя и сопротивление источника сигнала равны 1 кОм.
Дано:
Rн=10 кОм
F=30 Гц
Мн ≤ 6 дБ
Rвых = Rист =1 кОм
Rвх=470 кОм
Ср1-? Ср2-?
Решение:
Воспользуемся формулой коэффициента частотных искажений:
Мн
=
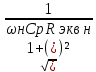 , где
Rэкв
н-эквивалентное
сопротивление контура на нижней частоте
, где
Rэкв
н-эквивалентное
сопротивление контура на нижней частоте
Для емкости на входе сопротивление Rэкв н вх = Rвх + Rист,
а для емкости на выходе Rэкв н вых = Rвых + Rн
Rэкв н вх = 470·103+1·103=471·103 ,Ом
Rэкв н вых = 1·103+10·103 =11·103 Ом
ωн=2πF –нижняя круговая частота
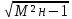 =
=
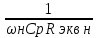 ,
,
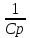 =
ωнRэкв
н
=
ωнRэкв
н
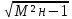 ,
Ср
=
,
Ср
=
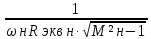 ,
,
Ср1
=
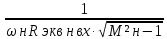 ,
Ср2
=
,
Ср2
=
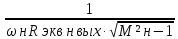
Мн=20log6(дБ)≈15,6 (раз), и так как по условию частотные искажения нужно поделить поровну между частотами, Мн=15,6/2= 7,8
Считаем разделительную емкость на входе:
Ср1
=
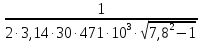 =
=
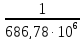 ≈
1,46 ·10-9
Ф
≈
1,46 ·10-9
Ф
Ср2
=
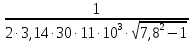 =
=
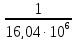 ≈
62,34 ·10-9
Ф
≈
62,34 ·10-9
Ф
Ответ: Ср1 = 1,46 нФ, Ср2 = 62,34 нФ
Задача 14.
Определить амплитуду напряжения гетеродина при которой коэффициент усиления транзисторного преобразователя частоты равен k0=12, если эквивалентное резонансное сопротивление контура Rэ=8кОм, коэффициенты включения контура m=1.n=0.3. Зависимость крутизны характеристики транзистора от напряжения гетеродина имеет вид: s=S0+aUr, где S0- значение крутизны при Uг=0, а=0.5 А/В. (в этой задаче косяк в условии!!!! Параметр а считаем за b!!!)))
Дано:
k0=12
Rэ=8кОм
m=1
n=0.3
b=0.5 А/В
s=S0+bUr
Uг-?
Решение:
Амплитуда напряжения гетеродина считается так:
Uг=bSпр , где где Sпр- крутизна преобразования
Sпр=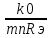 ,
→ Uг=
,
→ Uг=
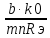 ,
Uг=
,
Uг=
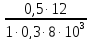 =
0,0025 В
=
0,0025 В
Ответ: Uг=2,5 мВ
Задача 15.
Определить избирательность преселектора при расстройке ∆fск=100кГц, если он содержит 2 одиночных контура и имеет полосу пропускания γN=100кГц на уровне γN=0,5.
Дано:
∆fск=100кГц
ПN=100кГц
γN=0,5
Sск-?
Решение:
Воспользуемся формулой избирательности по соседнему каналу для N контуров:
σ
ск N=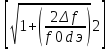 N
, т.
к. число контуров N=2,
то
N
, т.
к. число контуров N=2,
то
σ
ск N= 2
=
2
=
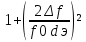
Из формулы полоса пропускания при заданной неравномерности для N контуров
ПγN=f0dэ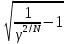 ,
где
dэ-эквивалентное
затухание контура,
,
где
dэ-эквивалентное
затухание контура,
f0-резонансная частота, найдем f0dэ:
f0dэ=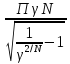 =
=
f0dэ=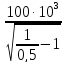 =
100·103
Гц
=
100·103
Гц
σ
ск
N=
1+
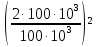 =
5
=
5
Ответ: σ ск N=5
Задача 16.
Определить полосу пропускания на уровне γN=0,707 преселектора, состоящего из одноконтурной входной цепи и одноконтурного УРЧ. Контуры входной цепи и УРЧ одинаковый каждый имеет полосу пропускания Пγ= 80 кГц на уровне γ=0.707.
Дано:
Пγ= 80 кГц
γN=0,707
П0,707-?
Решение:
Формула полосы пропускания на уровне 0,707:
П0,707=f0dэ,
А формула полоса пропускания при заданной неравномерности для N контуров
ПγN=f0dэ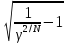 ,
где
dэ-эквивалентное
затухание контура,
,
где
dэ-эквивалентное
затухание контура,
f0-резонансная частота
при N=2
ПγN=f0dэ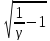 ,
→ полоса
одиночного контура П0,707=
f
0d
э
,
→ полоса
одиночного контура П0,707=
f
0d
э
f0dэ=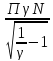 ,
,
П0,707=
f0dэ=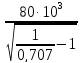 =51,5
·103
Гц
=51,5
·103
Гц
Ответ: П0,707=51,5 кГц
Задача 17
Рассчитать максимальную допустимую емкость нагрузки в усилителе звуковой частоты, если сопротивление нагрузки усилителя Rн=2 кОм, а допустимые низкочастотные искажения на частоте 10 кГц на весь усилитель Mв не более 3 дБ.
Дано:
Rн=2 кОм
F=10 кГц
Mв≤ 3дБ
Сн max-?
Решение:
Сн дает искажение на верхних частотах. Коэффициент частотных искажений на верхних частотах:
Mв
=
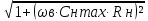 , ωв=2πF
, ωв=2πF
Выразим
емкость:
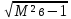 =
2πF
Сн
max
Rн
, Сн
max
=
=
2πF
Сн
max
Rн
, Сн
max
=
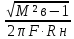
Mв (дБ)=103/20=1.41 (раз)
Сн
max
=
 ≈
7,9 ·10-9
Ф
≈
7,9 ·10-9
Ф
Ответ: Сн max =7,9 нФ
Задача 18
Определите полосу пропускания УРЧ на уровне γ = 0,707 на частоте f0=500кГц при следующих данных : m=0.5 ;n=0.2; Lk=200 мкГн ;Qk=100 ; Rвых VT1=10 кОм; Rвх сл=2 кОм
Дано:
γ = 0,707
f0=500кГц
m=0.5
n=0.2
Lk=200 мкГн
Qk=100
Rвых VT1=10 кОм
Rвх сл=2 кОм
Пγ-?
Решение:
Полоса пропускания на уровне 0,707 определяется так:
П0,707= f 0d э, где dэ-эквивалентное затухание контура
dэ для УРЧ:
dэ=dk
+m2ρ
G22
+ n2
ρ
Gн
, где
dk-затухание
контура dk
=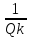 , dk=
, dk=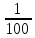 =0,01
=0,01
ρ-
характеристическое сопротивление
контура ρ=ωLk,
ω=2πf0
ρ=2·3.14·500·103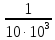 =314,2
Ом
=314,2
Ом
G22-выходная
проводимость G22=
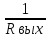 , G22=
, G22=
 =
0,1·10-3
1/Ом
=
0,1·10-3
1/Ом
Gн-
проводимость нагрузки Gн
=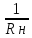 ,
RН=
Rвх
сл, Gн
=
,
RН=
Rвх
сл, Gн
=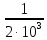 =
0,5·10-3
1/Ом
=
0,5·10-3
1/Ом
