1.2. Блочные матрицы

Предположим, что некоторая матрица при помощи горизонтальных и вертикальных прямых разбита на отдельные прямоугольные клетки, каждая из которых представляет собой матрицу меньших размеров и называется блоком исходной матрицы. В таком случае возникает возможность рассмотрения исходной матрицы A как некоторой новой (так называемой блочной) матрицы , элементами которой служат указанные блоки. Эти элементы обозначаются большой латинской буквой, чтобы подчеркнуть, что они являются матрицами, а не числами и им (как обычным элементам матрицы) приписываются два индекса, первый из которых указывает номер «блочной» строки, а второй — номер «блочного» столбца.

Например, матрицу

можно рассматривать как блочную матрицу

,

элементами которой служат следующие блоки:

Замечательным является тот факт, что основные операции с блочными матрицами совершаются по тем же правилам, по которым они совершаются с обычными матрицами, только в роли элементов выступают блоки.

1.3. Задачи

1. Для матриц A, B, C:

, ,

вычислить линейные комбинации: а) ;б) .

Найти произведение матриц , если оно определено:

2. ,.3. ,.

4. ,.5. ,.

Вычислить:

6. .7. .

8. Найти значение многочлена , если

, .

9. Какая из матриц А и В, является корнем многочлена :

, .

Найти все матрицы, перестановочные с А:

10. .11. .

Транспонировать матрицы и найти среди них симметричные:

12. .13. .14. .

Домашнее задание.

15. Для матриц A, B, C:

, ,

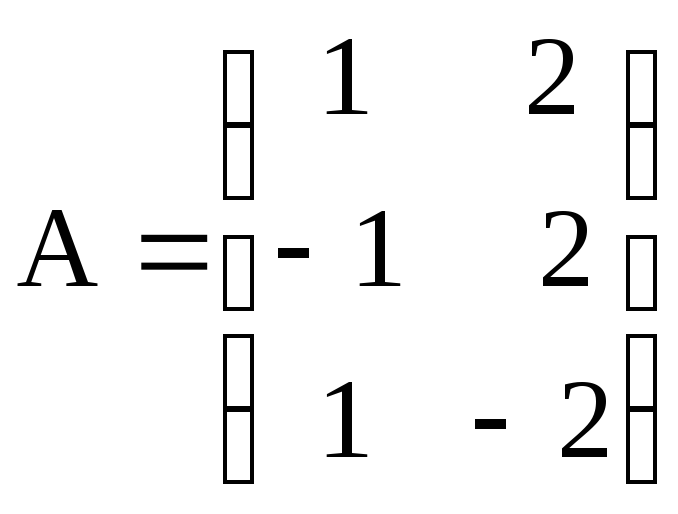вычислить: а) ;б) .

Найти произведение матриц и. Какие из пар матриц являются перестановочными:

16. ,.17. ,.

18. ,.19. ,.

20. Найти значение многочлена , если

, .

21. Найти значения и, при которых, если

, ,.

22. Для заданных матриц

, ,,

вычислить: а) ; б)в).

Ответы. 1. а) ; б). 2.. 3. Не определено.

4. . 5.. 6.. 7.. 8..

9. . 10., для любых. 11., для любых.

12. Не является симметричной. 13. Симметрична. 14. Не является симметричной.

15. а) ; б). 16., перестановочны. 17.,, не являются перестановочными.

18. , перестановочны. 19.,, не являются перестановочными. 20.. 21.,.

22. а) ; б); в).

1.4. Определители.

Для каждой квадратной матрицы порядка n вводится числовая характеристика, называемая определителем, соответствующим данной матрице. Для обозначения определителя используются символы: .

Введем понятие определителя, используя метод дедукции. При n=1, то есть когда матрица состоит из одного элемента , за значение определителя такой матрицы принимается числовое значение ее единственного элемента:. Далее, введем понятиеминора первого рода любого элемента матрицыкак определителя () –го порядка, соответствующего той матрице, которая получается вычеркиванием в матрицеi -той строки и j -го столбца, на пересечении которых стоит элемент . Обозначим его как. Например, для матрицы

минором является

(вычеркивается вторая строка и первый столбец). Назовем алгебраическим дополнением элемента выражениеи дадим следующее определение:Определителем порядка n, соответствующим матрице , называется число, равное :

.

Такое представление определителя называется разложением по первой строке. Легко проверить, что при n = 2: . При n = 3 миноры являются определителями второго порядка и легко вычисляются, поэтому можно получить специальную формулу для вычисления определителей третьего порядка, известную как«правило треугольника» (правило Саррюса). Алгоритм вычисления определителя для этого правила следующий: 1). Вычисляется сумма произведений элементов, расположенных на главной диагонали и в вершинах воображаемых треугольников, одно из оснований которых параллельно главной диагонали. 2). Вычисляется аналогичная сумма произведений элементов побочной диагонали и элементов, расположенных в вершинах треугольников, «параллельных» побочной диагонали. 3). Значение определителя равно разности указанных сумм.

При простых правил вычисления определителя нет и следует использовать общее правило - разложение по строке. При этом минорыявляются определителями третьего порядка, каждый из которых в свою очередь вычисляется либо разложением по первой строке, либо с помощью формулы треугольников. Очевидно, что с помощью разложения по строке можно вычислить определитель любого порядка, постепенно понижая порядок вычисляемых определителей.

Также имеет место

Tеорема: Каков бы ни был номер строки i (i = 1, 2, … , n) для определителя

n-го порядка справедлива формула

,

называемая разложением определителя по i -той строке.

Имеет место и аналогичная формула для вычисления определителя разложением по j-тому столбцу:

.

Докажем замечательное свойство разложения определителя по «чужой» строке или по «чужому» столбцу:

(1.1)

или

. (1.2)

Покажем справедливость равенства (1.1). Предварительно докажем, что определитель с двумя одинаковыми строками всегда равен нулю. Пусть в определителе

переставлены местами вторая и третья строки:

.

Разложим по второй строке, апо третьей. Тогда получим

, . Но, так как, а.

Итак, при перестановке двух строк (или столбцов) определитель меняет свой знак на противоположный. Поэтому, если две строки одинаковые, то, с одной стороны, при их перестановке значение определителя не меняется, а с другой, он меняет свой знак на противоположный, то есть и тогда. Вернемся теперь к нашему разложению определителя поi-той строке:

.

В данном разложении не зависит от элементовi-той строки, поскольку они вычеркиваются, поэтому, заменив в левой части строку на, получим, что определитель имеет две одинаковые строки, поэтому

.

Аналогично доказывается равенство (1.2). Свойство доказано.