
- •Глава 1. Алгебра матриц и линейные алгебраические уравнения
- •Матрицы.
- •1.1. Свойства матриц.
- •1.1.1. Некоторые свойства квадратных матриц.
- •1.2. Блочные матрицы
- •Например, матрицу
- •1.3. Задачи
- •Домашнее задание.
- •1.4. Определители.
- •1.4.1. Основные свойства определителей.
- •1.4.2. Способы вычисления определителей.
- •1.5. Задачи
- •Домашнее задание.
- •1.6. Обратная матрица.
- •1.7. Задачи
- •Домашнее задание.
- •1.8. Ранг матрицы.
- •1.8.1. Вычисление ранга матрицы.
- •1.9. Задачи
- •Домашнее задание.
- •1.10. Системы линейных алгебраических уравнений (слау).
- •1.10.1. Системы уравнений с квадратной матрицей.
- •1.10.2. Однородные системы.
- •1.10.3. Системы уравнений общего вида.
- •1.10.4. Метод Гаусса (метод исключения).
- •1.11. Задачи
- •Домашнее задание.
Глава 1. Алгебра матриц и линейные алгебраические уравнения
Линейная алгебра изучает свойства новых математических объектов – векторов и матриц, имеющих, в отличие от скаляров, внутреннюю структуру и действия с такими объектами. Скалярные величины являются простейшими математическими объектами, принимающими только числовые значения (целые, вещественные, положительные, отрицательные), и использование только скалярных величин является недостаточным для многих дисциплин, использующих математический аппарат. Так, понятие вектора используется в физике для описания силы, скорости, в геометрии – для описания положения точки в пространстве. Понятие матрицы вводится для описания объектов, имеющих внутреннюю структуру, например, в физике для описания состояния движущейся жидкости или газа, состояния электромагнитного поля, в математике – для представления систем линейных алгебраических уравнений и описания координатных преобразований векторов, а также во множестве других приложений.
Для изображения
математических объектов недостаточно
только букв того или иного алфавита, и
поэтому для этих целей широко используются
переменные с индексами, например:
![]() ,
гдеi,
k
- целые (положительные или отрицательные)
числа. Переменные с разными индексами,
даже обозначенные одними буквами,
считаются различными. Индексы могут
быть двойными, тройными, а также не
только нижними, но и верхними, с ними
допускаются арифметические действия.
,
гдеi,
k
- целые (положительные или отрицательные)
числа. Переменные с разными индексами,
даже обозначенные одними буквами,
считаются различными. Индексы могут
быть двойными, тройными, а также не
только нижними, но и верхними, с ними
допускаются арифметические действия.
Например:
![]() .
.
Для переменных с индексами вводятся сокращенные формы записи их сумм и произведений:
![]() ,
,
где индексы i, k, j, m пробегают всю заданную последовательность и их называют «немыми».
Матрицы.
Матрицей
называется совокупность элементов,
образующих двумерную структуру из m
строк и n
столбцов. Элементами матрицы могут быть
числа (числовая матрица), переменные
(скалярная матрица), функции (функциональная
матрица), сами матрицы (блочная матрица).
Обычно для изображения элементов матрицы
используется переменная с двумя нижними
индексами вида
![]() ,
которая называетсяобщим
элементом матрицы.
Ее первый индекс определяет номер строки
матрицы, второй – номер столбца, и
совокупность таких элементов образует
прямоугольную таблицу. Эта таблица
заключается в круглые, фигурные или в
двойные прямые скобки и в общем случае
имеет следующий вид:
,
которая называетсяобщим
элементом матрицы.
Ее первый индекс определяет номер строки
матрицы, второй – номер столбца, и
совокупность таких элементов образует
прямоугольную таблицу. Эта таблица
заключается в круглые, фигурные или в
двойные прямые скобки и в общем случае
имеет следующий вид:

Таким образом,
приведенная выше матрица имеет m
строк и n
столбцов. Если
![]() ,
то матрица называетсяпрямоугольной,
если же m
= n,
то квадратной.
Для обозначения матриц в целом, как
математического объекта, используются
заглавные (прописные) буквы. Сокращенная
форма записи может иметь следующий вид:
,
то матрица называетсяпрямоугольной,
если же m
= n,
то квадратной.
Для обозначения матриц в целом, как
математического объекта, используются
заглавные (прописные) буквы. Сокращенная
форма записи может иметь следующий вид:
![]() .
Значения индексов положительны и их
начальные значения всегда полагаются
равными единице. Поэтому матрицу
.
Значения индексов положительны и их
начальные значения всегда полагаются
равными единице. Поэтому матрицу![]() также можно записать в виде:
также можно записать в виде:![]() – матрица размерности
– матрица размерности![]() .
Если матрица квадратная, то естьm
= n,
то говорят, что
.
Если матрица квадратная, то естьm
= n,
то говорят, что
![]() – матрица размерностиn
или порядка n.
– матрица размерностиn
или порядка n.
Если матрица имеет
только одну строку
![]() ,
то ее называютвектор
– строкой,
если один столбец
,
то ее называютвектор
– строкой,
если один столбец
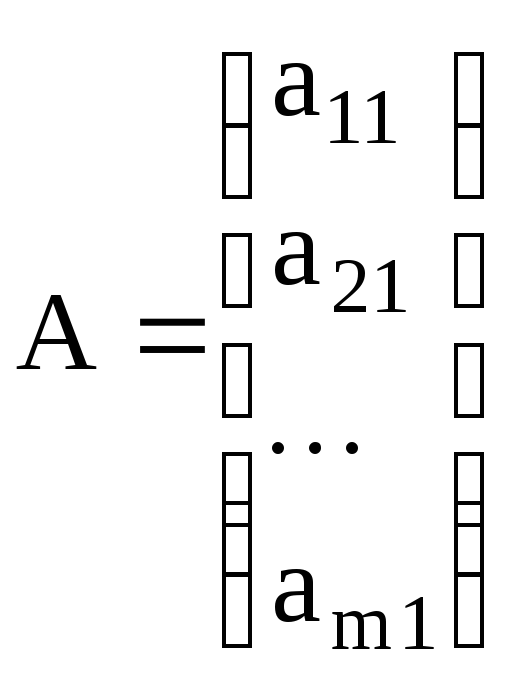 ,
товектор
– столбцом.
Если в матрице
,
товектор
– столбцом.
Если в матрице
![]() поменять местами строки и столбцы, то
полученная новая матрица называетсятранспонированной
по отношению к исходной матрице и
обозначается как
поменять местами строки и столбцы, то
полученная новая матрица называетсятранспонированной
по отношению к исходной матрице и
обозначается как
![]() .
Таким образом, если
.
Таким образом, если![]() ,
то
,
то![]() .
Размерности этих матриц в общем случае
различны. Например, если
.
Размерности этих матриц в общем случае
различны. Например, если![]() является вектор – строкой, то
является вектор – строкой, то![]() является вектор – столбцом.
является вектор – столбцом.
Нулевой называется матрица, все элементы которой равны нулю. Обозначается она буквой O, которую также часто обозначают нулем, однако подразумевая под ним нулевую матрицу.
