- •Учебно-методический комплекс Учебной дисциплины «Теория вероятностей и математическая статистика» Цикла ен по специальности
- •080107 «Налоги и налогообложение»
- •Рабочая учебная программа утверждаю:
- •Основание
- •Раздел 1. Элементы теории вероятностей
- •Раздел 2. Математическая статистика
- •2. Краткое изложение материала (сокращенный курс лекций)
- •Тема 1.Элементы комбинаторики
- •1.1. Размещения
- •1.2. Понятие факториала
- •1.3. Размещения с повторениями
- •1.4. Сочетания
- •Сочетания с повторениями
- •1.6. Перестановки
- •1.7. Перестановки с повторениями
- •1.8. Правила комбинаторики
- •Тема 2.Элементы теории вероятностей
- •2.1. Определение вероятности и свойства, вытекающие из её определения. Классификация событий. Диаграммы Венна
- •Полную группу можно определить так: если
- •2.2. Правила сложения и умножения вероятностей. Зависимые и независимые события
- •Тема 3. Формулы полной вероятности и байеса
- •Необходимо определить вероятность события а и переоценить вероятности событий Hi с учетом полной информации о событии а.
- •Тема 4. Дискретные случайные величины.
- •4.1. Определение дискретной случайной величины.
- •4.2.Числовые характеристики.
- •4.3. Математические операции над случайными величинами.
- •4.4. Распределения Бернулли и Пуассона.
- •4.5. Гипергеометрическое распределение.
- •5. Непрерывные случайные величины.
- •5.1. Функция распределения и плотность распределения непрерывной случайной величины.
- •5.2. Нормальное распределение
- •6. Вариационные ряды и их характеристики
- •6.1.Понятие вариационного ряда. Виды вариационных рядов.
- •6.2. Числовые характеристики вариационного ряда
- •7. Выборочный метод и статистическое оценивание
- •7.1. Основные понятия и определения выборочного метода
- •7.2. Статистическое оценивание
- •7.3. Ошибки выборки
- •Формулы расчёта ошибки выборки для собственно-случайного отбора
- •7.4. Определение численности (объема) выборки
- •Формулы расчёта необходимой численности выборки для собственно-случайного отбора
- •7.5. Интервальное оценивание
- •Тема 8. Проверка статистических гипотез
- •Статистическая проверка гипотез
- •3. Методические указания к выполнению курсовой работы, а также методические указания в целом
- •Задачи к теме 1 «Комбинаторика».
- •Задачи к теме 2 «Основные теоремы теории вероятностей».
- •Задачи к теме 3 «Формулы полной вероятности и Байеса».
- •Задачи к теме 4 «Законы распределения дискретных случайных величин».
- •Задачи к теме 5 «Законы распределения непрерывных случайных величин».
- •Задачи к теме 6 «Вариационные ряды и их характеристики».
- •Задачи к теме 7 «Выборочный метод и статистическое оценивание».
- •Задачи к теме 8 «Статистическая проверка гипотезы».
- •5. Контроль знаний (тесты, билеты, вопросы для экзамена, зачета) тесты
- •Тема 1. Комбинаторика
- •Тема 2. Основные определения, понятия и теоремы теории вероятностей
- •Тема 3. Формулы полной вероятности и Байеса
- •Тема 4. Случайные величины
- •Тема 5 . Закон больших чисел
- •Тема 6. Вариационный ряд и его числовые характеристики
- •Тема 7. Выборочный метод и его значение в экономических исследованиях
- •Тема 8. Статистическая проверка гипотез
- •Экзаменационные билеты
- •Вопросы к экзамену (зачету)
- •Раздел 1. Элементы теории вероятностей
- •Раздел 2. Математическая статистика
- •6. Сведения о ппс
- •7. Деловые игры и хозяйственные ситуации, используемые при проведении практических занятий
- •Дополнительный материал Глоссарий
- •Статистические таблицы
4.5. Гипергеометрическое распределение.
Пусть имеется множество N элементов, из которых М элементов обладают некоторым признаком A. Извлекается случайным образом без возвращения n элементов. Требуется найти вероятность того, что из них m элементов обладают признаком A. Искомая вероятность (зависящая от N, M, n, m) определяется по формуле:
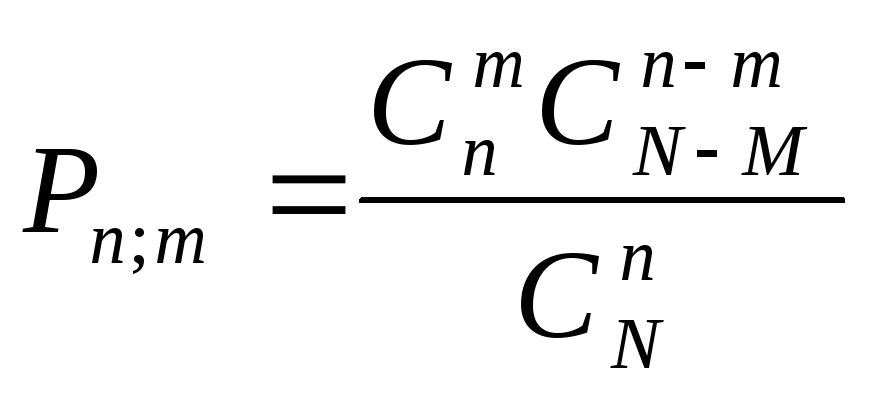 (4.15)
(4.15)
Если по формуле (4.15) вычислить вероятности для всех возможных значений m, то полученный ряд распределения называется гипергеометрическим законом распределения (таблица 4.5):
Таблица 4.5
|
M |
0 |
1 |
2 |
... |
n |
|
P(X=m) |
|
|
|
... |
|
Математическое ожидание и дисперсия случайной величины m, распределенной по гипергеометрическому закону, определяются формулами:
![]() (4.16)
(4.16)
![]() (4.17)
(4.17)![]()
5. Непрерывные случайные величины.
5.1. Функция распределения и плотность распределения непрерывной случайной величины.
Случайная величина Х называется непрерывной, если ее функция распределения непрерывна и имеет производную.
Как уже было
показано в разделе 4 (формула 4.2), функцией
распределения случайной величины Х
называется функция F(X), выражающая
вероятность выполнения условия
![]() :
:
![]() (5.1)
(5.1)
Функция распределения обладает следующими свойствами:
1.Вероятность
попадания случайной величины в промежуток
от
![]() до
до![]() равна приращению функции распределения
на концах этого промежутка:
равна приращению функции распределения
на концах этого промежутка:
![]() (5.2),
(5.2),
так как вероятность любого отдельного значения случайной величины равна нулю, если функция распределения непрерывна при этом значении, т. е. :
![]() ,
когда F(X) - непрерывна в точке
,
когда F(X) - непрерывна в точке
![]() =
=![]()
2.Функция распределения удовлетворяет условиям:
![]() (
5.3)
(
5.3)
Плотностью распределения (дифференциальной функцией)непрерывной случайной величины называется функция
f(x) =![]() (x).(5.4)
(x).(5.4)
Плотность
распределения любой случайной величины
неотрицательна:
![]()
Несобственный
интеграл от дифференциальной функции
в пределах от -![]() до +
до +![]() равен 1:
равен 1:
![]() (5.5)
(5.5)
График функции y = f(x) называется кривой распределенияили графиком плотности распределения. Кривая y = f (x) располагается над осью абсцисс.
Вероятность
попадания случайной величины в промежуток
от
![]() до
до![]() может быть вычислена по формуле:
может быть вычислена по формуле:
![]() (5.6)
(5.6)
Подинтегральное
выражение f(x)dxназывается элементом
вероятности. Оно выражает вероятность
попадания случайной точки в промежуток
между точками х и![]() , где
, где![]() бесконечно малая величина.
бесконечно малая величина.
Функция распределения F(x) выражается через плотность f(x) формулой :
![]() (5.7)
(5.7)
Математическое ожидание непрерывной случайной величины Х вычисляется по формуле:
![]() (5.8),
(5.8),
дисперсия
![]() (5.9)
(5.9)
5.2. Нормальное распределение
Если плотность распределения (дифференциальная функция) случайной переменной определяется выражением:
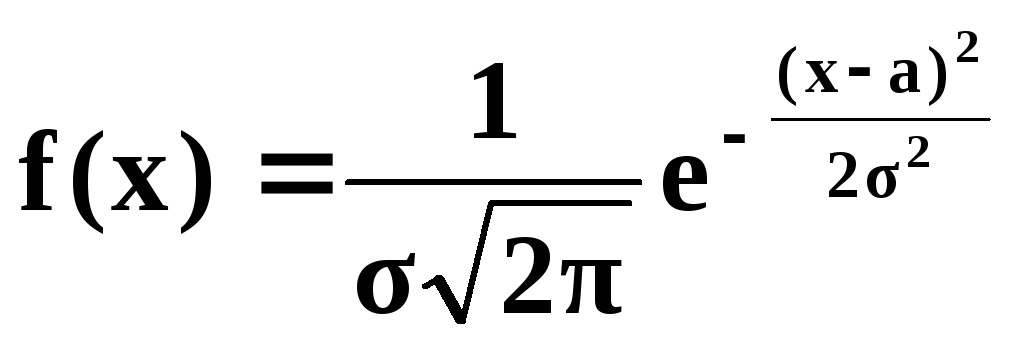 (5.10)
(5.10)
то говорят, что Х
имеет нормальное распределение с
параметрами а и![]() .
Вероятностный смысл параметров:
.
Вероятностный смысл параметров:
![]() =М(X),
а
=М(X),
а![]() .Обозначение:
.Обозначение:
![]()
Для расчета
вероятности попадания нормально
распределенной случайной величины Х
в промежуток от
![]() до
до![]() используется формула:
используется формула:
![]() (5.11)
(5.11)
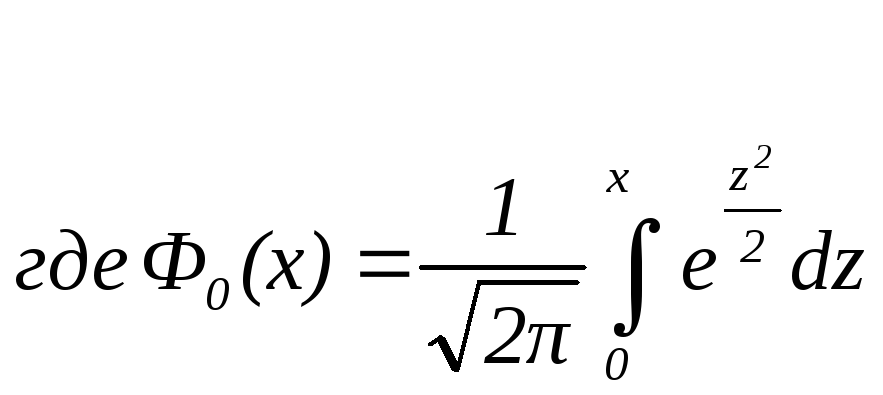 (интеграл
Лапласа)
(интеграл
Лапласа)
Формула (5.11) иногда в литературе называется интегральной теоремой Лапласа.
Функция
![]() обладает свойствами:
обладает свойствами:
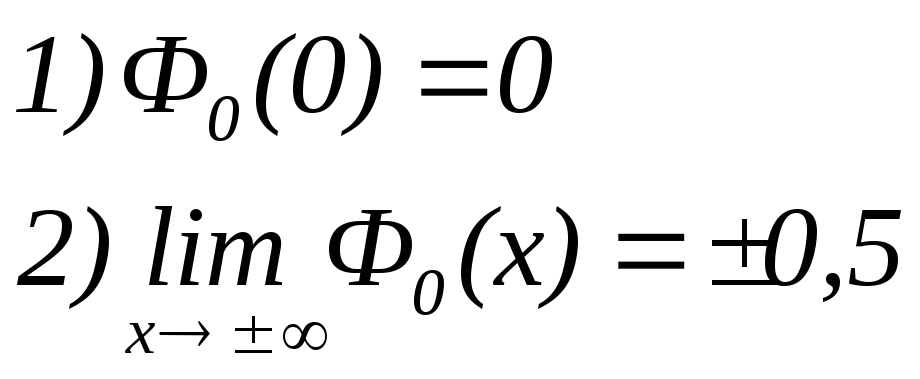
3)![]() (см. таблицу приложения 2).
(см. таблицу приложения 2).
Функция
![]() табулирована. В частности для симметричного
относительно а промежутка
табулирована. В частности для симметричного
относительно а промежутка![]() имеем:
имеем:
![]() (5.12)
(5.12)
Формула (5.12) применима и к частоте m,поскольку ее закон распределения при достаточно большом числе испытаний практически совпадает с нормальным. Применительно к случайной величинеm, с учетом ее числовых характеристик
M(m)
= npи![]() (5.13)
(5.13)
формула (5.12) примет вид :
![]() (5.14)
(5.14)
Формула (5.12) может
быть применена и к относительной частоте
![]() с числовыми характеристиками
с числовыми характеристиками![]() и
и![]()
![]()
![]() (5.15)
(5.15)
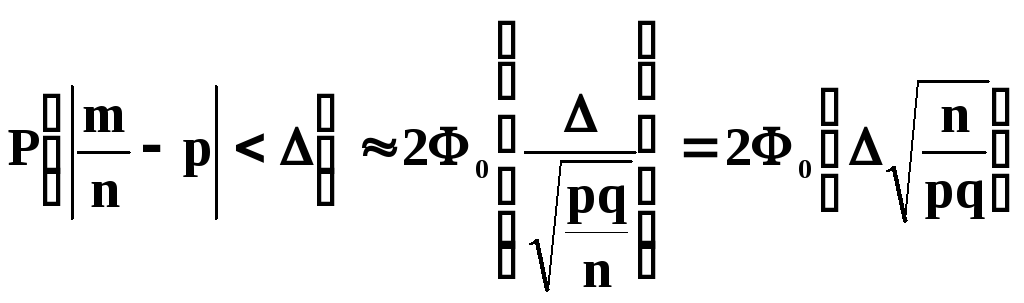 (5.16)
(5.16)
С вероятностью,
очень близкой к единице (равной
![]() нормально
распределенная случайная величина Х
удовлетворяет неравенству:
нормально
распределенная случайная величина Х
удовлетворяет неравенству:
![]() (5.17)
(5.17)
В этом состоит
правило трех сигм: если случайная
величина распределена по нормальному
закону, то ее отклонение от математического
ожидания практически не превышает![]() .
.
Локальная теорема
Муавра-Лапласа.При р![]() и p
и p![]() 1
и достаточно большом n биноминальное
распределение близко к нормальному
закону (причем их математические ожидания
и дисперсии совпадают), т.е. имеет место
равенство:
1
и достаточно большом n биноминальное
распределение близко к нормальному
закону (причем их математические ожидания
и дисперсии совпадают), т.е. имеет место
равенство:
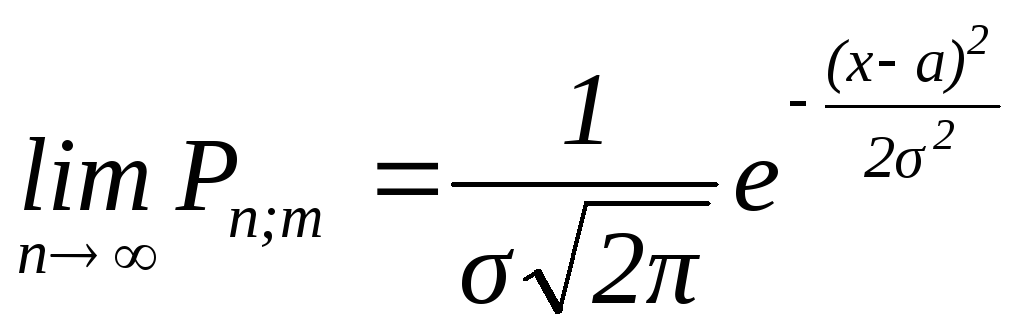 ,
где
,
где
![]() ,a=nр
,a=nр
Тогда:
![]() (5.18)
(5.18)
для
достаточно больших n (здесь
![]() (х)
- плотность вероятностей стандартной
нормальной случайной величины
(х)
- плотность вероятностей стандартной
нормальной случайной величины![]() и
и![]() ).
).